Ортогональная проекция окружности

<10 11 121314 15 16 >

Как известно, параллельной проекцией окружности является кривая, называемая эллипсом. Поскольку ортогональная проекция является частным случаем параллельной, то очевидно, что ортогональной проекцией окружности будет тоже эллипс. Так, проецируя окружность, расположенную в плоскости S с центром в точке D, ортогонально на плоскость П¢, получим эллипс с центром в точке D¢ в соответствии с рисунком 1.3.28.

Рассмотрим в окружности два взаимно перпендикулярных диаметра AB и CD, причём АВ проходит по прямой уровня плоскости S (по прямой h), т.е. АВ||П¢. Следовательно, А¢В¢=АВ=d, где d – диаметр окружности. Диаметр CD как перпендикулярный к АВ, являющийся линией уровня плоскости S, называется также линией наибольшего наклонаданной плоскости к плоскости проекций П¢. Такое название объясняется тем, что среди различных прямых плоскости S линия наибольшего наклона CD, перпендикулярная к линии уровня АВ, образует наибольший угол с плоскостью проекций П¢. Угол j, образованный диаметром окружности CD и диаметром эллипса C¢D¢ как проекцией CD, является линейным углом двугранного угла наклона плоскости S к плоскости П¢. Тогда C¢D¢=CD·cosj, но CD=АВ=d, следовательно C¢D¢=d·cosj.

Как известно, взаимно перпендикулярные диаметры окружности обладают свойством сопряжённости (каждый сопряжённый диаметр делит пополам хорды, параллельные другому диаметру), это свойство при параллельном проецировании сохраняется, следовательно, диаметры А¢В¢ и C¢D¢ будут сопряжёнными диаметрами эллипса.

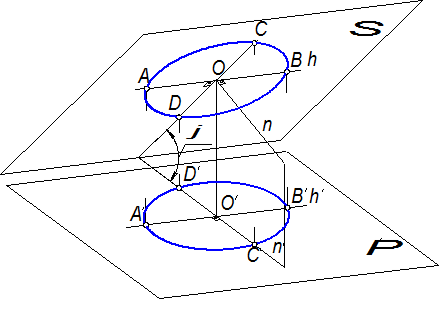
Рисунок 1.3.29 – Ортогональная проекция окружности

Но с другой стороны, эти диаметры взаимно перпендикулярны, так как являются проекциями взаимно перпендикулярных диаметров, один из которых параллелен плоскости проекций, поэтому они являются осями эллипса, причём А¢В¢ – большая ось, C¢D¢ – малая ось.

Если провести какую-нибудь прямую n, перпендикулярную к плоскости S в соответствии с рисунком 1.3.29, то такая прямая будет перпендикулярна ко всякой прямой плоскости S, в частности, будет перпендикулярна к диаметру АВ||П¢. Поэтому её ортогональная проекция n¢ на плоскость П¢ окажется прямой, перпендикулярной к проекции А¢В¢ диаметра АВ. Иначе говоря, проекция прямой, перпендикулярной к плоскости S, параллельна малой оси эллипса.

Таким образом, большая ось эллипса, являющегося ортогональной проекцией окружности, плоскость S которой составляет угол j с плоскостью проекций, параллельна проекции линии уровня плоскости Sи равна диаметру окружности, а малая ось параллельна проекции перпендикуляра к плоскости S и равна d·cosj.

Рассмотрим соотношение осей полученного эллипса:

Для данных плоскостей S и П¢ угол j и cosj – величины постоянные. Вследствие этого cosj может служить характеристикой отношения осей эллипса, которое, в свою очередь, характеризует форму эллипса.

Итак, как бы ни была расположена окружность в плоскости S, на плоскости проекций всегда будет получаться эллипс одной и той же формы. Следует отметить, что при данном угле j не только форма эллипса будет постоянной, но и расположение осей также не будет зависеть от размеров и положения окружности в плоскости S.

Если угол j увеличивать, то эллипс, имея постоянной большую ось, будет становиться всё уже. В пределе, когда угол j станет равным 90°, а cosj=0, т.е. плоскость S перпендикулярна плоскости П¢, окружность будет проецироваться в отрезок.

Если cosj=1, то плоскость S параллельна плоскости проекций и эллипс-проекция принимает форму окружности.

Рассмотрим построение окружности, расположенной в проецирующей плоскости в соответствии с рисунком 1.3.30, а.

Пусть окружность с центром в точке О и радиусом R лежит во фронтально проецирующей плоскости S(S₂). Выберем два взаимно перпендикулярных диаметра окружности АВ и CD, из которых АВ||П₂, а CD||П₁. Таким образом, диаметр CD совпадает с горизонталью плоскости S, а АВ – с линией наибольшего наклона к плоскости П₁.

Рисунок 1.3.30 - Окружность в проецирующей плоскости

Тогда проекциями диаметра АВ будут служить отрезки А₁В₁ и А₂В₂=АВ=2R, диаметр CD спроецируется на П₂ в точку С₂ºD₂=0, а на плоскость П₁ в отрезок С₁D₁=CD=2R.

Таким образом в данном случае фронтальной проекцией окружности является отрезок прямой длиной 2R, горизонтальной проекцией – эллипс,

большой осью которого служит отрезок С₁D₁, малой осью – отрезок А₁В₁. Заметим, что малая ось А₁В₁ эллипса совпадает с проекцией n₁перпендикуляра n к плоскости S. Промежуточные точки эллипса можно построить при помощи двух концентрических окружностей, проведённых на осях С₁D₁ и А₁В₁ как на диаметрах.

Аналогично строят проекции окружности, расположенной в горизонтально проецирующей плоскости Q(Q₁), в соответствии с рисунком 1.3.30, б.

<10 11 121314 15 16 >

Дата добавления: 2017-02-13; просмотров: 2402;