Взаимопринадлежность (инцидентность) точки и плоскости

Если точка принадлежит плоскости в пространстве, то проекции этой точки принадлежат соответствующим проекциям какой-либо прямой, лежащей в данной плоскости (в соответствии с рисунком 1.3.16 прямая АВ и принадлежащая ей точка 1; прямая ВС и принадлежащая ей точка 2). В данном примере и точка М принадлежит плоскости треугольника АВС, т.к. точка М расположена на прямой А-2, лежащей в плоскости треугольника. При этом следует отметить, что плоскость безгранична, поэтому некоторые построения могут выходить за пределы треугольника.

Прямая А-2 является фронталью плоскости треугольника АВС (горизонтальная проекция этой прямой А₁2₁ параллельна воображаемой оси проекций х₁₂). Точка К принадлежит данной фронтали (К₁Îf₁ и К₂Îf₂) и, следовательно, принадлежит плоскости треугольника АВС. Как видно, точка К принадлежит и прямой С-1 данного треугольника. Эта прямая является горизонталью (фронтальная проекция прямой С₂1₂ параллельна воображаемой оси х₁₂).

Очевидно, через каждую точку плоскости можно провести одну горизонталь и одну фронталь, лежащие в этой плоскости в соответствии с рисунком 1.3.16.

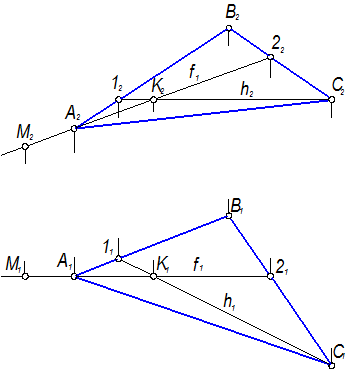
Рисунок 1.3.16 – Принадлежность точки плоскости

Следы плоскости

Следом плоскости называется прямая её пересечения с плоскостью проекций. На рисунке 1.3.17 плоскость W задана следами l и m: l=W ∩П₂ и m=W ∩П₁, а М=W ∩х₁₂ – точка пересечения плоскости W с осью проекций х₁₂.

Точка М, принадлежащая одновременно обеим плоскостям проекций, должна, очевидно, лежать на обоих следах плоскости W. Следовательно, следы плоскости W пересекаются на оси: m∩l=М, МÎх₁₂. Для задания плоскости следами достаточно дать горизонтальную проекцию горизонтального следа и фронтальную проекцию фронтального следа, так как другие проекции следов совпадают с осью х₁₂ в соответствии с рисунком 1.3.17.

Нетрудно видеть, след на горизонтальной плоскости проекций П₁ является не чем иным, как горизонталью h данной плоскости, а след на фронтальной плоскости проекций П₂ является её фронталью f. Задание плоскости её следами на плоскостях проекций является частным случаем задания плоскости двумя пересекающимися прямыми, а именно пересекающимися прямыми уровня.

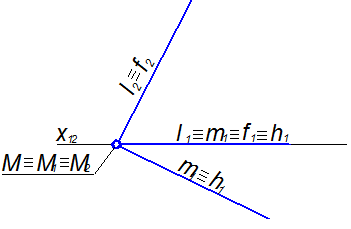
Рисунок 1.3.17 – Следы плоскости