КИНЕМАТИКА КРИВОШИПНО-ШАТУННОГО МЕХАНИЗМА

Кривошипно-шатунный механизм (KШM) является основным механизмом поршневого ДВС, который воспринимает и передает значительные по величине нагрузки. Поэтому расчет прочности KШM имеет важное значение. В свою очередь расчеты многих деталей двигателя зависят от кинематики и динамики КШМ. Кинематический анализ КШМ устанавливает законы движения его звеньев, в первую очередь поршня и шатуна.

Для упрощения исследования КШМ будем считать, что кривошипы коленчатого вала вращаются равномерно, т. е. с постоянной угловой скоростью.

11.1. Типы КШМ

В поршневых ДВС применяются три типа КШМ:

• центральный (аксиальный);

• смешанный (дезаксиальный);

• с прицепным шатуном.

В центральном КШМ ось цилиндра пересекается с осью коленчатого вала (рис. 11.1).

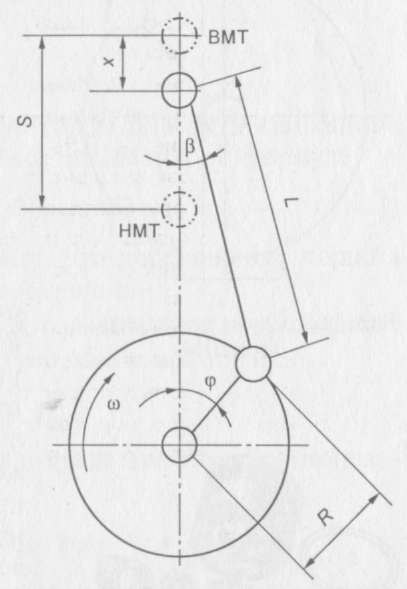
Рис. 11.1. Схема центрального КШМ: φ — текущий угол поворота коленчатого вала; β — угол отклонения оси шатуна от оси цилиндра (при отклонении шатуна в направлении вращения кривошипа угол β считается положительным, в противоположном направлении — отрицательным); S — ход поршня;
R — радиус кривошипа; L — длина шатуна; х — перемещение поршня;

ω — угловая скорость коленчатого вала

Угловая скорость рассчитывается по формуле

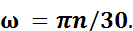
Важным конструктивным параметром КШМ является отношение радиуса кривошипа к длине шатуна:

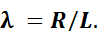
Установлено, что с уменьшением λ (за счет увеличения L) происходит снижение инерционных и нормальных сил. При этом увеличивается высота двигателя и его масса, поэтому в автомобильных двигателях принимают λ от 0,23 до 0,3.

Значения λ для некоторых автомобильных и тракторных двигателей приведены в табл. 11.1.

Таблица 11.1. Значения параметра λ для различных двигателей

Двигатель	λ
ВАЗ-2106	0,295
ЗИЛ-130	0,257
Д-20	0,280
СМД-14	0,28
ЯМЗ-240	0,264
КамАЗ-740	0,2167

В дезаксиальном КШМ (рис. 11.2) ось цилиндра не пересекает ось коленчатого вала и смещена относительно ее на расстояние а.

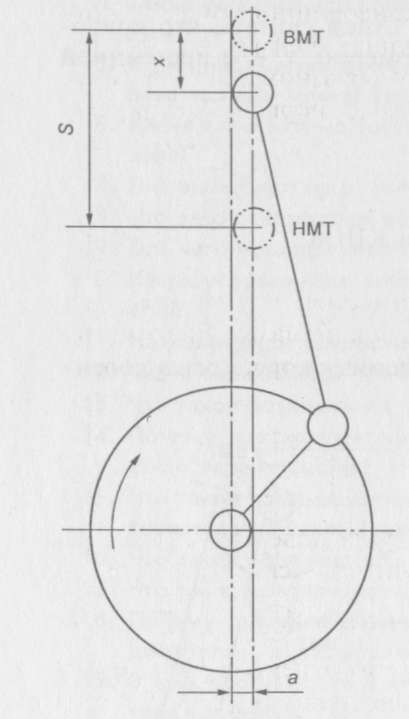
Рис. 11.2. Схема дезаксиального КШМ

Дезаксиальные КШМ имеют относительно центральных КШМ некоторые преимущества:

• увеличенное расстояние между коленчатым и распределительным валами, в результате чего увеличивается пространство для перемещения нижней головки шатуна;

• более равномерный износ цилиндров двигателя;

• при одинаковых значениях R и λ больше ход поршня, что способствует снижению содержания токсичных веществ в отработавших газах двигателя;

• увеличенный рабочий объем двигателя.

На рис. 11.3 показан КШМ с прицепным шатуном. Шатун, который шарнирно соединен непосредственно с шейкой коленчатого вала, называется главным, а шатун, который соединен с главным посредством пальца, расположенного на его головке, называется прицепным. Такая схема КШМ применяется на двигателях с большим числом цилиндров, когда хотят уменьшить длину двигателя. Поршни, соединенные с главным и прицепным шатуном имеют не одинаковый ход, так как ось кривошипной головки прицепного шатуна при работе описывает эллипс, большая полуось которого больше радиуса кривошипа. В V-образном двенадцатицилиндровом двигателе Д-12 разница в ходе поршней составляет 6,7 мм.

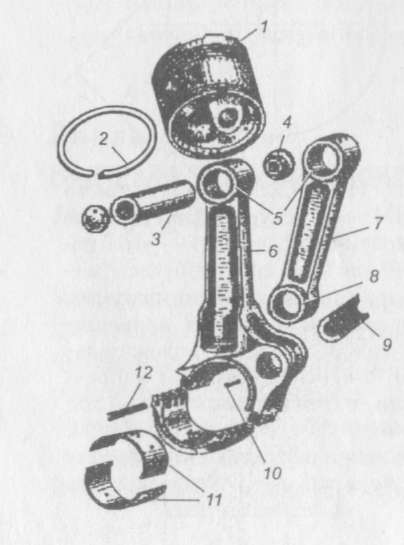
Рис. 11.3. КШМ с прицепным шатуном: 1 — поршень; 2 — компрессионное кольцо; 3 — поршневой палец; 4 — заглушка поршневого пальца; 5 — втулка верхней головки шатуна; 6 — главный шатун; 7 — прицепной шатун; 8 — втулка нижней головки прицепного шатуна; 9 — палец крепления прицепного шатуна; 10 — установочный штифт; 11 — вкладыши; 12— конический штифт

11.2. Кинематика центрального КШМ

При кинематическом анализе КШМ считается, что угловая скорость коленчатого вала постоянна. В задачу кинематического расчета входит определение перемещения поршня, скорости его движения и ускорения.

11.2.1. Перемещение поршня

Перемещение поршня в зависимости от угла поворота кривошипа для двигателя с центральным КШМ рассчитывается по формуле

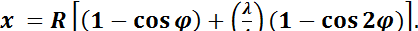(11.1)

Анализ уравнения (11.1) показывает, что перемещение поршня можно представить как сумму двух перемещений:

x₁ — перемещение первого порядка, соответствует перемещению поршня при бесконечно длинном шатуне (L = ∞ при λ = 0):

;

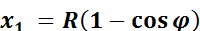х₂ — перемещение второго порядка, представляет собой поправку на конечную длину шатуна:

;

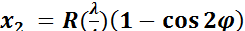Величина х₂ зависит от λ. При заданном λ экстремальные значения х₂ будут иметь место, если

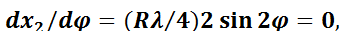
т. е. в пределах одного оборота экстремальные значения х₂ будут соответствовать углам поворота (φ) 0; 90; 180 и 270°.

Максимальных значений перемещение достигнет при φ = 90° и φ = 270°, т. е. когда соs φ = -1. В этих случаях действительное перемещение поршня составит

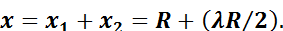
Величина λR/2, называется поправкой Брикса и является поправкой на конечную длину шатуна.

На рис. 11.4 показана зависимость перемещения поршня от угла поворота коленчатого вала. При повороте кривошипа на 90° поршень проходит больше половины своего хода. Это объясняется тем, что при повороте кривошипа от ВМТ до НМТ поршень движется под действием перемещения шатуна вдоль оси цилиндра и отклонения его от этой оси. В первой четверти окружности (от 0 до 90°) шатун одновременно с перемещением к коленчатому валу отклоняется от оси цилиндра, причем оба перемещения шатуна соответствуют движению поршня в одном направлении, и поршень проходит больше половины своего пути. При движении кривошипа во второй четверти окружности (от 90 до 180°) направления движений шатуна и поршня не совпадают, поршень проходит наименьший путь.

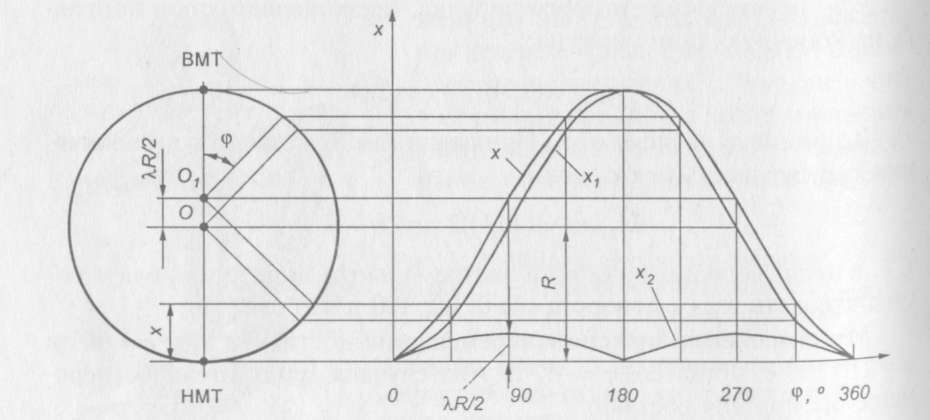
Рис. 11.4. Зависимость перемещения поршня и его составляющих от угла поворота коленчатого вала

Перемещение поршня для каждого из углов поворота может быть определено графическим путем, которое получило название метод Брикса. Для этого из центра окружности радиусом R=S/2 откладывается в сторону НМТ поправка Брикса, находится новый центр О₁. Из центра О₁ через определенные значения φ (например, через каждые 30°) проводят радиус-вектор до пересечения с окружностью. Проекции точек пересечения на ось цилиндра (линия ВМТ—НМТ) дают искомые положения поршня при данных значениях угла φ. Использование современных автоматизированных вычислительных средств позволяет быстро получить зависимость x=f(φ).

11.2.2. Скорость поршня

Производная перемещения поршня — уравнение (11.1) по времени вращения дает скорость перемещения поршня:

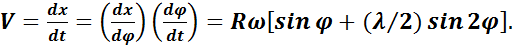(11.2)

Аналогично перемещению поршня скорость поршня может быть представлена также в виде двух составляющих:

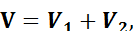
где V₁– составляющая скорости поршня первого порядка:

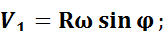
V₂ — составляющая скорости поршня второго порядка:

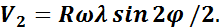
Составляющая V₂ представляет собой скорость поршня при бесконечно длинном шатуне. Составляющая V₂ является поправкой к скорости поршня на конечную длину шатуна. Зависимость изменения скорости поршня от угла поворота коленчатого вала показана на рис. 11.5.

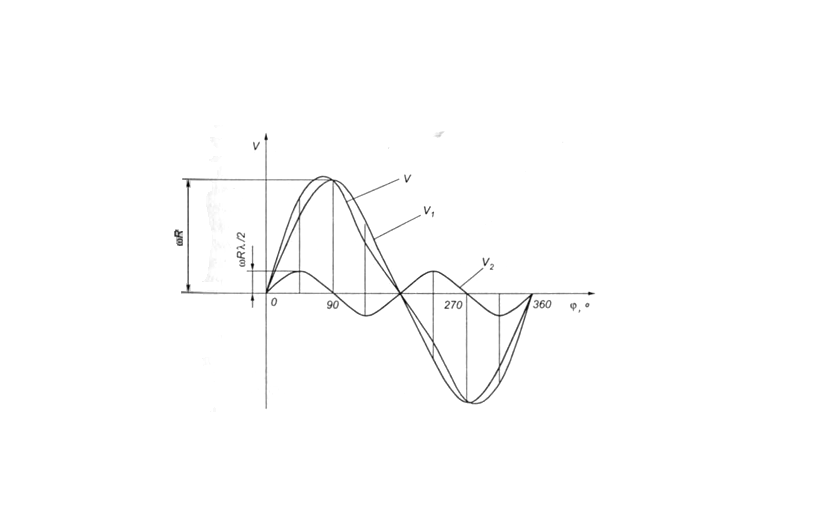
Рис. 11.5. Зависимость скорости поршня от угла поворота коленчатого вала

Максимальные значения скорость достигает при углах поворота коленчатого вала меньше 90 и больше 270°. Точное значение этих углов зависит от величин λ. Для λ от 0,2 до 0,3 максимальные скорости поршня соответствуют углам поворота коленчатого вала 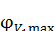от 70 до 80° и 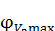от 280 до 287°.

Средняя скорость поршня рассчитывается следующим образом:

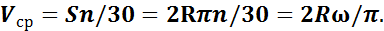
Средняя скорость поршня в автомобильных двигателях обычно находится в пределе от 8 и до 15 м/с. Значение максимальной скорости поршня с достаточной точностью может быть определено как

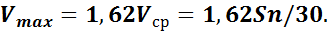
11.2.3. Ускорение поршня

Ускорение поршня определяется как первая производная скорости по времени или как вторая производная перемещения поршня по времени:

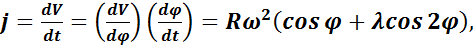(11.3)

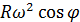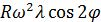где и — гармонические составляющие первого и второго порядка ускорения поршня соответственно j₁ и j₂. При этом первая составляющая выражает ускорение поршня при бесконечно длинном шатуне, а вторая составляющая — поправку ускорения на конечную длину шатуна.

Зависимости изменения ускорения поршня и его составляющих от угла поворота коленчатого вала показаны на рис. 11.6.

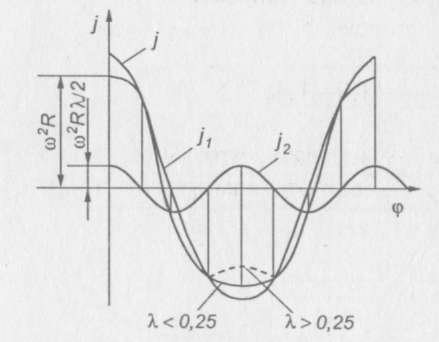
Рис. 11.6. Зависимости изменения ускорения поршня и его составляющих
от угла поворота коленчатого вала

Ускорение достигает максимальных значений при положении поршня в ВМТ, а минимальных — в НМТ или около НМТ. Эти изменения кривой j на участке от 180 до ±45° зависят от величины λ. При λ > 0,25 кривая j имеет вогнутую форму в сторону оси φ (седло), и ускорение достигает минимальных значений дважды. При λ = 0,25 кривая ускорения выпуклая, и ускорение достигает наибольшего отрицательного значения только один раз. Максимальные ускорения поршня в автомобильных ДВС 10 000 м/с² . Кинематика дезаксиального КШМ и КШМ с прицепным шатуном несколько отличается от кинематики центрального КШМ и в настоящем издании не рассматривается.

11.3. Отношение хода поршня к диаметру цилиндра

Отношение хода поршня S к диаметру цилиндра D является одним из основных параметров, который определяет размеры и массу двигателя. В автомобильных двигателях значения S/D от 0,8 до 1,2. Двигатели с S/D > 1 называются длинноходными, а с S/D < 1 — короткоходными. Данное отношение непосредственно влияет на скорость поршня, а значит и мощность двигателя. С уменьшением значения S/D очевидны следующие преимущества:

• уменьшается высота двигателя;

• за счет уменьшения средней скорости поршня снижаются механические потери и уменьшается износ деталей;

• улучшаются условия размещения клапанов и создаются предпосылки для увеличения их размеров;

• появляется возможность увеличения диаметра коренных и шатунных шеек, что повышает жесткость коленчатого вала.

Однако есть и отрицательные моменты:

• увеличивается длина двигателя и длина коленчатого вала;

• повышаются нагрузки на детали от сил давления газа и от сил инерции;

• уменьшается высота камеры сгорания и ухудшается ее форма, что в карбюраторных двигателях приводит к повышению склонности к детонации, а в дизелях — к ухудшению условий смесеобразования.

Целесообразным считается уменьшение значения S/D при повышении быстроходности двигателя. Особенно это выгодно для V-образных двигателей, где увеличение короткоходности позволяет получить оптимальные массовые и габаритные показатели.

Значения S/D для различных двигателей:

• карбюраторные двигатели — 0,7—1;

• дизели средней быстроходности — 1,0—1,4;

• быстроходные дизели — 0,75—1,05.

При выборе значений S/D следует учитывать, что силы, действующие в КШМ, в большей степени зависят от диаметра цилиндра и в меньшей — от хода поршня.

<== предыдущая лекция	\|	следующая лекция ==>
Взаимосвязь совокупного спроса и совокупного предложения в равновесной точке	\|	Сущность и функции денег

Дата добавления: 2017-02-13; просмотров: 16380;