Графическое исследование кинематики рядного механизма.
Изобразим в масштабе 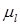 ,мм/м, кинематическую схему рядного зубчатого механизма. Нанесем на эту схему линейную скорость точки P1, изобразив ее в произвольном масштабе
,мм/м, кинематическую схему рядного зубчатого механизма. Нанесем на эту схему линейную скорость точки P1, изобразив ее в произвольном масштабе 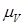 , мм/м*с-1 отрезком Р1Р1’ Соединим конец этого отрезка точкуР1’ центрами вращения колес 1 и 2 точками 01и 02 и получим прямые, определяющие распределение линейных скоростей этих звеньев, для точек лежащих на линии центров. Эти прямые образуют с линией центров соответственно углы
, мм/м*с-1 отрезком Р1Р1’ Соединим конец этого отрезка точкуР1’ центрами вращения колес 1 и 2 точками 01и 02 и получим прямые, определяющие распределение линейных скоростей этих звеньев, для точек лежащих на линии центров. Эти прямые образуют с линией центров соответственно углы 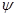 1 и
1 и 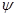 2 . Точка Р2является точкой касания начальных окружностей колес 3 и 4. Так как в точке касания начальных окружностей линейные скорости звеньев 2 и 3 равны, а распределение линейных скоростей по линии центров для звена 2 известно, то можно определить отрезок Р2Р2’,который изображает скорость точки Р2 в масштабе
2 . Точка Р2является точкой касания начальных окружностей колес 3 и 4. Так как в точке касания начальных окружностей линейные скорости звеньев 2 и 3 равны, а распределение линейных скоростей по линии центров для звена 2 известно, то можно определить отрезок Р2Р2’,который изображает скорость точки Р2 в масштабе 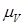 , мм/м*с-1. Соединив прямой точку Р2’ с центром вращения звена 3 получим прямую распределения линейных скоростей для точек звена 3, лежащих на линии центров. Угол, который образует эта прямой с линией центров, обозначим
, мм/м*с-1. Соединив прямой точку Р2’ с центром вращения звена 3 получим прямую распределения линейных скоростей для точек звена 3, лежащих на линии центров. Угол, который образует эта прямой с линией центров, обозначим 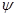 3 . Угловые скорости звеньев определятся из этой графической расчётной схемы по формулам:
3 . Угловые скорости звеньев определятся из этой графической расчётной схемы по формулам:
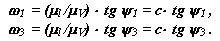
Передаточное отношение, рассматриваемого рядного зубчатого механизма, будет равно:
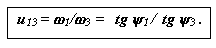
Формула Виллиса.
Формула Виллиса выводится на основании основной теоремы зацепления и устанавливает соотношение между угловыми скоростями зубчатых колес в планетарном механизме. Рассмотрим простейший планетарный механизм с одним внешним зацеплением (см. рис. 17.3). Число подвижностей в этом механизме равно:
Wпл = 3 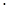 n – 2
n – 2 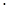 p1 – 1
p1 – 1 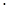 p2 = 3
p2 = 3 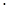 3 – 2
3 – 2 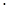 3 – 1
3 – 1 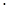 1 = 2,
1 = 2,
то есть для получения определенности движения звеньев механизма необходимо сообщить независимые движения двум его звеньям. Рассмотрим движение звеньев механизма относительно стойки и относительно водила. Обозначение угловых скоростей звеньев в каждом из рассматриваемых движений приведены в таблице 17.2.
Таблица 17.2
| Движение механизма | Звено 1 | Звено 2 | Звено 3 | Звено 4 |
| Относительно стойки | 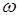 1 1
| 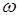 2 2
| 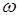 h h
| 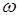 0 =0 0 =0
|
| Относительно водила | 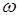 *1= *1= 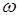 1- 1- 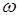 h h
| 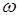 *2= *2= 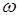 2- 2- 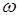 h h
| 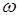 h- h- 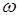 h=0 h=0
| - 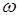 h h
|
В движении звеньев относительно водила угловые скорости звеньев равны угловым скоростям в движении относительно стойки минус угловая скорость водила. Если в движении относительно стойки ось зубчатого колеса 2 подвижна, то в движении относительно водила оси обоих зубчатых колес неподвижны. Поэтому к движению относительно водила можно применить основную теорему зацепления.
Дата добавления: 2017-02-13; просмотров: 1022;











