Эффекты самовоздействия, параметрические эффекты и вынужденное рассеяние.

Наряду с появлением «лишних» частот в спектре сигнала, проходящего через нелинейную среду, имеют место и эффекты «самовоздействия» излучения, выражающиеся в том, что оптические свойства среды изменяются по отношению к распространению самого интенсивного сигнала. Для объяснения «самовоздействия» достаточно представления поляризации в скалярном приближении:

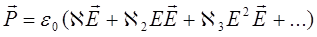(14.42)

Вклад в поляризуемость среды на частоте ω дают первый и третий члены (линейная и кубичная восприимчивость). Наличие члена с 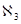эквивалентно появлению в ε(ω) и n(ω) слагаемого, пропорционального 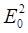, т.е.

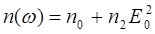(14.43)

Иначе говоря, ограниченный интенсивный пучок света делает среду оптически неоднородной. Но в таком случае на продольной «виртуальной»

(Е₀ = 0) границе пучка возможно полное внутреннее отражение – в том случае, если n₂ > 0. Если, аналогично волоконной оптике, ввести «угол скольжения» 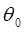, то условие полного отражения на виртуальной границе можно записать как

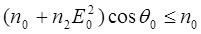
(14.44)

(см. рисунок 14.6). В параксиальном приближении 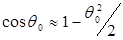, поэтому 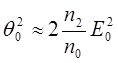(14.45)

С другой стороны, факт ограниченности пучка по диаметру можно трактовать как наличие диафрагмы, вызывающей дифракцию Френеля. Пучок при этом расходится, и предельный угол отклонения от оптической оси можно оценить как

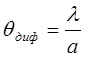(14.46)

где а – диаметр пучка.

Что же получается? Самофокусировка вызывает сжатие пучка, а дифракция — расширение. Следовательно, наблюдать самофокусировку можно только при 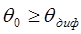, т.е. самофокусировка носит пороговый характер. Порог самофокусировки оценивается в параксиальном приближении из условия

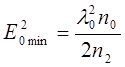(14.47)

Отсюда по известному значению n₂ для нелинейной среды можно оценить минимальную мощность светового пучка, необходимую для наблюдения самофокусировки. При Е₀ = Е_0min площадь сечения пучка при распространении в среде остается постоянной, т.е. пучок сам себе создает световод, в котором отсутствует дифракционная расходимость. Такой режим естественно назвать самоканализацией пучка. При Е₀ > Е_0min наблюдается самофокусировка, причем лучи искривляются в сторону оптической оси, и эффект усугубляется. Среда ведет себя как собирающая линза с переменным фокусным расстоянием (рисунок 14.7).

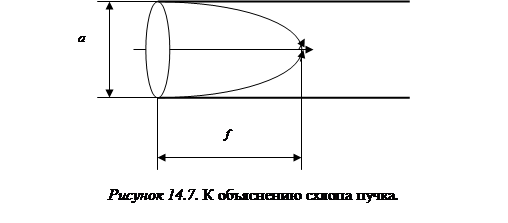
Поскольку 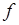~ 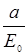, искривление лучей по мере приближения к оптической оси увеличивается. Следовательно, изменяя входную интенсивность, можно управлять положением фокуса (приближать его к месту входа пучка в среду). Это явление, наблюдавшееся экспериментально при прохождении через среду мощных лазерных импульсов (впервые в 1965 г. Н.М. Пилипецким и А.Р. Рустамовым в сероуглероде в режиме свободной генерации рубинового лазера) было образно названо А.М. Прохоровым «бегущим фокусом». Скорость перемещения фокуса в случае коротких импульсов может быть сделана оценочно очень большой (вплоть до субсветовых скоростей). Однако фактическое движение фокуса наблюдаемо в относительно небольших пределах, поскольку при достижении значений Е₀, сопоставимых с внутриатомными (а это не так уж много — порядка 10⁴ … 10⁵ В/см), возникает пробой и разрушение среды в области фокуса. Так что любимый вопрос студентов: а можно ли разогнать фокус при очень малых (фемтосекундных) длительностях до сверхсветовых скоростей? — следует признать некорректным. Схлоп пучка, т.е. пробой и разрушение среды произойдет гораздо раньше, чем разгон фокуса до релятивистских скоростей.

Для нашего случая, т.е. распространения пучка в биосредах, гораздо интереснее вопрос об определении n₂ в таких средах, где в области резонансного поглощения возможно его резкое увеличение. Особенностью биосред является то, что такие области резонансного поглощения расположены в сравнительно легко достижимом диапазоне длин волн (для твердотельных либо эксимерных лазеров, работающих в комбинации с лазерами на красителях), поэтому даже слабые с точки зрения оптических сред поля могут вызывать нелинейные эффекты. Но желаемый диапазон длин волн может быть достигнут не только за счет выбора соответствующих активных сред, но и за счет самих нелинейных эффектов. В самом деле, процедура расчета как самих полей, так и характеристик сред в общем аналогична уже проделанной нами при расчете интенсивности высших гармоник. В зависимости от начальных и граничных условий система уравнений Максвелла в нулевом приближении дает то или иное волновое решение для амплитуды поля 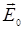( 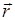,t). Для нахождения следующего приближения в правые части материальных уравнений Максвелла подставляется поляризация вида (14.1), где Е( 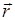, t) заменено найденным выражением из нулевого приближения. Тем самым получаются неоднородные уравнения с известными правыми частями. Эти правые части можно рассматривать как дополнительные источники волн, обусловленные нелинейной поляризуемостью среды. Элемент объема среды dV излучает как диполь с моментом 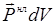. Соответствующие решения уравнений Максвелла нужно искать в виде волн с частотами w, 2w, 3w …, поскольку эти частоты присутствуют в нелинейных осцилляциях диполя .

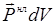Рассмотренный выше случай генерации 2-й гармоники представляет собой частный случай распространения в нелинейной среде двух волн с частотами w₁ и w₂ при w₁ = w₂. Если же w₁ ¹ w₂, то, помимо основных и кратных частот, в спектре вынужденных колебаний появляются суммарная и разностная частоты. Такое взаимодействие можно трактовать как следствие изменения оптических параметров среды под действием сильного поля одной из волн (w₁). В результате возникает модуляция с частотой w₁ фазы второй волны (w₂), что эквивалентно появлению боковых компонент w₁ - w₂ и w₁ + w₂. Практический интерес процессов генерации суммарных и разностных частот обусловлен тем, что при смешении излучения двух лазеров в нелинейной среде получается когерентное излучение в новом (отличном от w₁ и w₂ диапазоне спектра). Тем самым можно расширить диапазон доступных источников когерентного излучения, не разрабатывая целиком новых лазеров, т.е. не изыскивая новых генерационных переходов.Такая параметрическая генерация получила широкое распространение, начиная с 1962 г. Впервые такие лазеры были созданы группой Е.М. Швома, одного из основоположников прикладной нелинейной оптики и создателей НИИ «Полюс» — ведущего предприятия в электронной промышленности СССР по лазерной технике.

Другое, не менее важное, применение нелинейного преобразования частоты — это повышение чувствительности фотоприемных устройств. При нелинейном взаимодействии сильного w₁ и слабого w₂ сигналов амплитуда сигнала разностной частоты возрастает пропорционально корню из произведения амплитуд каждого из сигналов. Если слабый сигнал w₂ находится за пределами чувствительности фотоприемного устройства, то путем увеличения амплитуды сигнала w₁ можно уверенно обнаружить w₂ за счет нелинейного взаимодействия. Такой метод регистрации слабых сигналов был впервые предложен Форрестером (Forrester A.T.) в 1961 г. и получил название оптического гетеродинирования, по аналогии с радиодиапазоном.

Справедливости ради следует отметить, что идея оптического гетеродинирования была высказана значительно раньше (Г.С. Горелик, 1947 г.), однако в то время экспериментальное осуществление этой идеи не удалось, поскольку интенсивность некогерентных источников оказалась недостаточной. Ситуация коренным образом изменилась с появлением лазеров — Форрестер еще с 40-х годов очень внимательно отнесся к идеям Горелика и немедленно по появлении неон-гелиевых лазеров осуществил эксперимент по наблюдению межмодовых биений с выделением разностной частоты сильной и слабой мод.

В нашей стране развитие методики оптического гетеродинирования связано прежде всего с именами В.С. Летохова и В.П. Чеботаева, под руководством которых было создано целое новое направление в науке — нелинейная лазерная спектроскопия, а также Л.Н. Курбатова и В.Е. Зуева, под руководством которых были проведены пионерские исследования в части применения оптического гетеродинирования для целей локации и связи. Биомедицинские применения оптического гетеродинирования (в лазерной диагностике) будут более подробно рассмотрены ниже.

Наряду с регистрацией слабых сигналов параметрику можно использовать и для непосредственного усиления слабой волны w₁ или w₂ за счет перекачки энергии из сильной волны w₃ . Впервые такой метод параметрического усиления света был предложен С.А. Ахмановым и Р.В. Хохловым в 1962 г. Взаимодействие сильной волны с частотой w₃ и слабой (сигнальной) волны с частотой w₁ за счет квадратичной восприимчивости 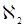приведет к появлению в нелинейной поляризуемости осцилляций на разностной частоте w₂ = w₃ - w₁ . При выполнении векторного условия пространственного синхронизма 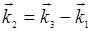вторичные волны с частотой w₂, испускаемые в направлении 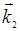, складываются синфазно. В результате возникает резонансная перекачка энергии. На квантовом языке параметрическое усиление можно рассматривать как вынужденный распад фотона ħw₃ на фотоны ħw₁ и ħw₂. Соотношение w₃ = w₁ +w₂ в таком процессе выражает закон сохранения энергии, 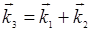- сохранения импульса.

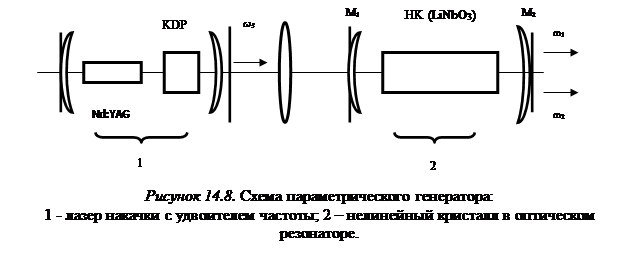
Одна из возможных схем параметрического генератора показана на рисунке 14.8.

Нелинейный кристалл LiNbO₃ (2) расположен в резонаторе как активный элемент. Для волн, распространяющихся в направлении оптической оси, выполняется условие пространственного синхронизма 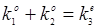. Зеркала М₁ и М₂ имеют высокие коэффициенты отражения для частот w₁ и w₂. Зеркало М₁ прозрачно для частоты w₃ излучения накачки (1). При достаточно большой мощности излучения накачки параметрическое усиление одной из волн w₁ или w₂ на длине нелинейного кристалла превышает однопроходные потери, выполняя тем самым условие самовозбуждения. Поскольку в направлении, перпендикулярном плоскости зеркал, выполняется условие фазового синхронизма, при небольшом изменении ориентации зеркал относительно оптической оси или других управляющих воздействиях (наложении внешнего электрического или магнитного поля, изменении температуры и т.п.) частоты w₁ и w₂ изменяются. Полоса перестройки определяется тем диапазоном, для которого в данном нелинейном кристалле выполняется условие пространственного синхронизма. Этот диапазон плавной перестройки обычно гораздо больше традиционного диапазона перестройки частоты генерации в пределах одной линии рабочего перехода при изменении длины резонатора, поскольку частота w₃ при этом остается постоянной. Заметим при этом, что выполнение условия пространственного синхронизма для кристалла НК накладывает жесткие требования к источнику накачки в части высокой монохроматичности и малой пространственной расходимости. Смягчение этих требований вызывает резкое возрастание пороговой мощности накачки и снижение КПД.

Разработанные на основе высококачественных нелинейных кристаллов LiNbO₃ (ниобат лития), Ba₂NaNb₅O₁₅ («банан»), KDP (дигидрофосфат калия), ADP (дигидрофосфат аммония) параметрические генераторы света позволяют получать когерентное излучение с плавной перестройкой частоты при задающем лазере на второй гармонике Nd:YAG во всем видимом и значительной части ИК диапазона спектра.

Еще один класс нелинейных явлений — это процессы вынужденного рассеяния.

Пусть в среде распространяется упругая плоская монохроматическая волна с частотой Ω и волновым вектором 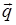. Ее фазовая скорость 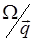— это скорость звука v , определяемая упругими характеристиками среды (модулем Юнга) и средней плотностью ρ. Периодические изменения плотности 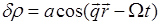приводят к пространственной модуляции показателя преломления среды δn ~ δρ , т.е. создают фазовую дифракционную решетку. При падении монохроматического света 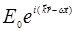на такую решетку появляется дифрагированная волна 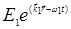с волновым вектором 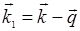и частотой 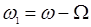(если угол между 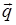и 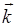острый). Если же угол между 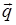и 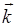тупой, то дифрагированная волна характеризуется вектором 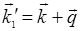и частотой 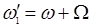. Если упругие волны обусловлены тепловым движением частиц среды (а мы помним, что в конденсированных средах из-за сильной связи между частицами среды тепловое движение можно рассматривать как совокупность всевозможных упругих волн, занимающих диапазон частот от нескольких герц до 10¹⁰…10¹¹ Гц), то наблюдаемое на таких волнах рассеяние света называется рассеянием Мандельштама-Бриллюэна. Указанное рассеяние было предсказано теоретически независимо друг от друга названными учеными и экспериментально открыто также независимо друг от друга в 1928 г. Л.И. Мандельштамом и Г.С. Ландсбергом в СССР и Раманом в Индии. Рассеяние Мандельштама-Бриллюэна можно трактовать как рассеяние фотона исходного пучка света на неоднородностях среды с испусканием или поглощением фонона — кванта упругих колебаний среды — с импульсом ħ 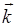и энергией ħΩ. В элементарном акте рассеяния выполняются законы сохранения энергии и импульса:

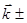ħ 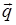ħ =ħ ;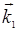

ħω ± ħΩ = ħω₁

Если упругие колебания возбуждаются независимо, то рассеяние Мандельштама-Бриллюэна называется спонтанным, или классическим. При этом вероятность испускания фонона и появления рассеянного фотона не зависит от интенсивности падающего излучения. Тем самым классическое МБ-рассеяние является линейным процессом.

Если же упругая волна в кристалле вызывается мощным лазерным излучением, причем она когерентна падающей световой волне, то такое рассеяние называется вынужденным рассеянием Мандельштама-Бриллюэна (ВРМБ). ВРМБ было открыто на опыте в 1964 г. Чиао, Таунсом и Стойчевым. Тогда же было установлено, что ВРМБ носит ярко выраженный пороговый характер и наблюдается только при превышении некоторой критической интенсивности падающего света. Процесс ВРМБ можно рассматривать как перекачку энергии от волны ω к волнам Ω и ω-Ω, т.е. как аналог параметрического усиления. Волну Ω в этом случае имеет смысл рассматривать как волну создаваемого светом давления, распространяющуюся в том же направлении и с той же скоростью, что и первичная упругая волна, благодаря которой возникла рассеянная световая волна. При достаточно большой интенсивности исходного пучка света, когда усиление для волн Ω и ω-Ω превысит потери, амплитуды этих волн по мере распространения в среде будут возрастать. Поскольку, в отличие от классического РМБ, возникающее при ВРМБ излуче
ние когерентно, можно обеспечить положительную обратную связь между усиливаемыми световой и упругой волнами.

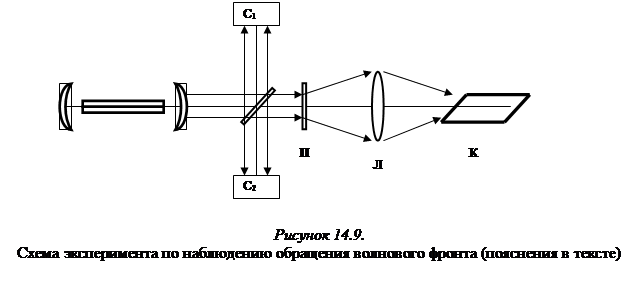
Для биомедицинских применений наибольший интерес представляет случай рассеяния назад. В этом случае усиливаемые волны распространяются навстречу друг другу. Если падающий первичный пучок пространственно неоднороден, т.е. характеризуется неравномерным распределением интенсивности поперек оптической оси, то при ВРМБ имеет место обращение волнового фронта (ОВФ), не имеющее аналога в классической оптике. Схема эксперимента по наблюдению ОВФ показана на рисунке 14.9.

Лазерный пучок проходит через делительное зеркало, отражающее небольшую его часть на измерительную систему С₁, регистрирующую угловое распределение интенсивности излучения в дальней зоне. Проходящая часть пучка попадает на фазовую пластинку П со случайными неоднородностями. Расходимость пучка при этом возрастает в десятки раз. Затем линза Л с большой апертурой, достаточной для того, чтобы перехватить весь пучок, направляет излучение в кювету К, заполненную сероуглеродом или метаном при высоком давлении. Рассеянный назад свет отражается от делительного зеркала и регистрируется измерительной системой С₂, аналогичной системе С₁. Сравнение распределений, зарегистрированных системами С₁ и С₂, показало, что первоначально широкий пучок рассеянного света после прохождения через те же оптические элементы в обратной последовательности становится столь же направленным, как и первоначальный лазерный пучок. Так происходит потому, что волновой фронт излучения, рассеянного назад в нелинейной среде, в точности воспроизводит сколь угодно сложную структуру волнового фронта падающей волны, отличаясь лишь противоположным направлением распространения (уменьшение частоты на величину порядка 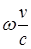, где v - скорость звука, а с – скорость света, можно не принимать во внимание). Этот изящный эксперимент, осуществленный впервые С.А. Ахмановым и Р.В. Хохловым, можно по научной значимости сравнить с первым наблюдением голографических картин. По образному выражению Р.В. Хохлова, «кювету с рассеивающим веществом можно рассматривать как волшебное зеркало, изменяющее знак времени». Эффект обращения волнового фронта уточняет представления о необратимых и обратимых оптических явлениях. Информация о первоначальной структуре когерентного светового пучка не теряется при прохождении через фазовую пластинку. Механизм вынужденного рассеяния обращает искаженный волновой фронтс сохранением этой информации. При прохождении в обратном направлении через ту же пластинку все внесенные ею искажения волнового фронта полностью компенсируются, и пучок восстанавливает свою структуру, т.е. возвращается в исходное состояние, но обращенное во времени.

С помощью обращения волнового фронта в нелинейной среде можно получить предельно малую расходимость излучения мощных лазеров с оптически неоднородными активными средами. Случайные неоднородности активной среды искажают волновой фронт и ухудшают направленность выходного пучка. Воспользуемся описанным явлением для ликвидации этого ухудшения. Именно, пропустим пучок от задающего маломощного лазера через мощный оптический усилитель с такой случайно-неоднородной средой. После обращения волнового фронта в нелинейной среде излучение вновь пропустим через тот же усилитель в противоположном направлении. При этом одновременно с дальнейшим увеличением интенсивности происходит компенсация искажений волнового фронта, и выходящее излучение имеет направленность, аналогичную направленности пучка от задающего лазера (а в силу маломощности этот пучок легко сделать минимально, т.е. дифракционно расходящимся). Таким методом были получены рекордные по фокусировке в предельно малом объеме результаты концентрации мощного излучения.

Наряду с ВРМБ в начале 60-х годов было открыто явление вынужденного комбинационного рассеяния (ВКР). Аналогично ВРМБ, классический случай комбинационного рассеяния представляет собой появление в спектре рассеянного света линий, сдвинутых относительно частоты падающего излучения ω на частоту собственных колебаний молекул среды Ω. Само по себе происхождение этих линий легко объяснить индуцированными падающим излучением осцилляциями дипольного момента молекул, в результате которых рассеянное излучение оказывается промодулированным по частоте:

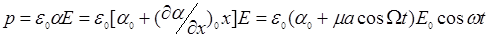, (14.48)

где α — поляризуемость среды, меняющаяся по гармоническому закону с частотой Ω при отклонении атомов в молекуле от равновесного положения по тому же закону 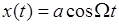, μ = 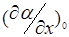— коэффициент, характеризующий изменение поляризуемости при смещении атомов из равновесного положения, α₀ — поляризуемость в равновесной конфигурации.

В квантовых представлениях, стоксова компонента с частотой (ω – Ω) возникает при уменьшении энергии фотона ħω на величину энергии кванта колебаний молекулы ħΩ, антистоксова (ω + Ω) — при передаче энергии кванта первоначально возбужденной молекулы излучению. В классике интенсивность антистоксовой компоненты, пропорциональная числу возбужденных молекул, много меньше интенсивности стоксовой, поскольку соотношение числа возбужденных и невозбужденных молекул в равновесии подчиняется формуле Больцмана 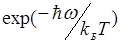« 1.

ВКР, в отличие от классики, также дает испускание стоксовой и антистоксовой спектральных компонент, но с вероятностью процесса, зависящей от интенсивности падающего излучения. Как и ВРМБ, ВКР возникает только при интенсивности падающего излучения, превышающей некоторую пороговую величину. При этом доля рассеянного излучения достигает десятков процентов (при 10^-7 … 10^-8 от интенсивности падающего света в классическом случае). Как и полагается при нелинейных взаимодействиях, в рассеянном излучении наблюдаются не только частоты (ω ± Ω), но и (ω ± 2Ω) и т.д. Рассеяние имеет четко выраженный направленный характер. Это объясняется интерференцией вторичных волн, испускаемых диполями в различных точках рассеивающей среды, т.е. опять возникает условие фазового синхронизма.

Для стоксова излучения выполнение условия фазового синхронизма наилучшим образом обеспечивается при совпадении направлений падающего и рассеянного излучения, поскольку при параллельности пучков объем среды, где происходит их наложение, много больше, чем для внеосевого направления. Для антистоксовой компоненты в среде с нормальной дисперсией условие фазового синхронизма наилучшим образом выполняется в направлениях, составляющих небольшой угол с возбуждающим пучком (например, в нитробензоле для излучения рубинового лазера этот угол составлял 3⁰), поэтому при наблюдении ВКР возможно пространственное разделение стоксовой и антистоксовой компонент при сравнимых между собой интенсивностях. Интересно, что исторически ВКР было обнаружено раньше, чем ВРМБ, поскольку оно обычно сопровождается другими нелинейными явлениями, благодаря которым порог наблюдения понижается.

Литература к лекции 14.

1. Д.В. Сивухин. Общий курс физики, т.4. Оптика.

2. А. Ярив. Введение в оптическую электронику. Пер. с англ., М., Высшая школа, 1983.

3. Справочник по лазерам под ред акад. А.М. Прохорова, т.2, М., Сов. Радио, 1978.