Генерация оптических гармоник.

ПОНЯТИЕ О НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ ЭФФЕКТАХ.

Нелинейные оптические эффекты проявились практически сразу, как только началось более-менее систематическое изучение свойств лазерного излучения (с 1961 г.). Во-первых, они выступают как ограничитель возможностей роста энергетических характеристик излучения, во-вторых, — как качественно новый, ранее невозможный способ извлечения информации о свойствах среды, взаимодействующей с лазерным излучением. С первой точки зрения нелинейные эффекты — зло, и с ними следует неуклонно бороться, со второй — большое благо, поскольку открывается особый «служебный вход» в кладовую информации о свойствах материи. Диалектика работает!

Второй аспект разрабатывался значительно активнее первого, поэтому как фундаментальные, так и прикладные перспективы развития нелинейной оптики были обрисованы уже с 1962 г., когда появились классические труды академика Р.В. Хохлова и его ученика и последователя С.А. Ахманова в СССР и — чуть позднее — Н. Бломбергена за рубежом.

Справедливости ради следует отметить также, что ряд нелинейных эффектов (например, самофокусировка) был предсказан и получен экспериментально еще раньше, в работах Н.Г. Басова и А.М. Прохорова.

Современная ситуация в науке существенно отличается от 60-х годов, когда при всем желании зарубежные исследователи не могли игнорировать наших достижений. Поэтому в процессе чтения различных ретроспекций очень рекомендую вам быть особенно внимательными именно к описанию этого времени. Тогда ни одно серьезное научное мероприятие не обходилось без приглашения наших ученых, что сегодня усиленно замалчивается. В полной мере это относится к нелинейной оптике. Особенно быстрыми темпами развивалась прикладная нелинейная оптика. Наиболее яркий пример — генерация оптических гармоник.

Если в первых экспериментах 1961 г. удвоение частоты рубинового лазера было обнаружено с помощью весьма тонких измерений (коэффициент преобразования по мощности основного излучения с l = 694 нм во вторую гармонику с l = 347 нм не превышал 10^-11), то уже в 1963 г. были созданы удвоители частоты с КПД, достигавшим 10%. В последующие годы были созданы умножители частоты лазерного излучения, позволившие перекрыть диапазон от дальнего ИК до вакуумного ультрафиолета и работающие во всех режимах (от непрерывного до пикосекундных импульсов). Сегодня уже совершенно невозможно представить себе квантовую электронику и когерентную оптику без оптических умножителей частоты, применяемых в самых разнообразных лазерных системах.

Имея в виду перспективы развития лазерной диагностики (еще только чуть-чуть затронутые), нельзя не отметить следующий исключительно важный для применения в медицине и биологии аспект. На первых порах главные успехи нелинейной оптики были связаны с использованием нелинейных оптических кристаллов. Это естественно, поскольку в кристаллах концентрация активных частиц наибольшая(~10²² см^-3), поэтому зависимость оптических характеристик материала от внешнего электрического поля должна проявиться там раньше всего.

Классифицируя нелинейные взаимодействия с помощью разложения поляризации P(t) по полю Е(t),

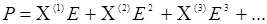(14.1)

можно сказать, что главные успехи прикладной нелинейной оптики связаны с использованием эффектов, описываемых квадратичной нелинейной восприимчивостью Χ⁽²⁾. Таковые проявляются в кристаллах, не обладающих центром инверсии. Однако в ряде случаев представляют особый интерес и взаимодействия более высокого порядка. Дело в том, что большие возможности управления нелинейной восприимчивостью возникают за счет использования резонансных взаимодействий. Эти взаимодействия не дают большого выигрыша в конденсированных средах, где ширина линий разрешенных переходов обычно велика (вспомним, что наивысшая степень монохроматичности и стабильности частоты может быть получена в газовых лазерах на нейтральных атомах). Поэтому увеличение нелинейных восприимчивостей, обусловленных близостью частот взаимодействия к атомному или молекулярному резонансу, в газовой среде можно сделать аномально большим. Соответствующие эксперименты показали, что можно добиться КПД преобразования в 3-ю гармонику за счет резонансного взаимодействия в парах щелочных металлов и благородных газов порядка 40-50%, причем при значительно меньших уровнях мощности, чем в случае кристаллических умножителей частоты. Газовые нелинейные оптические устройства позволяют еще более расширить возможности получения когерентного излучения в оптическом диапазоне (от дальнего ИК до мягкого рентгеновского) и тем самым обеспечить уникальные возможности исследования свойств биологических объектов. Добавим к этому, что сами оптические свойства биотканей в силу специфики взаимодействия с лазерным излучением (см. ниже) начинают зависеть от интенсивности падающего излучения при ничтожно малых по сравнению с кристаллами интенсивностях, поэтому нелинейная оптика биологических сред – это такая область оптики, которая еще ждет своего бурного развития, и вообще-то весьма парадоксально то, что нелинейная оптика кристаллов – наиболее прозрачных и, следовательно, наиболее «упорных» с точки зрения интенсивности падающего излучения сред – уже давно стала классикой, а нелинейная оптика биосред, выпирающая наружу практически в каждом случае лазерного облучения биообъекта, застряла на уровне накопления экспериментальных данных. Дело-то, получается, за вами, входящими в третье тысячелетие!

Рассмотрим подробнее возможность генерации второй гармоники (ГВГ) при прохождении лазерного излучения через кристалл.

Поляризация диэлектрических кристаллов обусловлена главным образом перемещениями валентных электронов атомов под действием внешнего поля – среда рассматривается как совокупность элементарных диполей. Обозначим: x – смещение электрона от положения равновесия, N – плотность электронов. Тогда поляризацию можно записать в виде

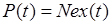(14.2)

Здесь e – заряд электрона.

В симметричных кристаллах потенциальная энергия электрона может быть записана в виде

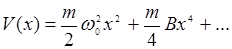(14.3)

где ω₀ – резонансная частота электронного осциллятора, В – постоянная, m – масса электрона. Кристалл с потенциалом вида (14.3), очевидно, обладает свойством V(x) = V(-x). Вообще говоря, он не обязан быть симметричным, т.е. в зависимости V(x) могут появиться нечетные степени x:

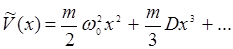(14.4)

В случае (14.3) на электрон действует возвращающая сила

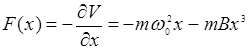+… (14.5)

а в случае (14.4) –

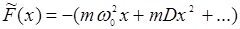(14.6)

Линейная поляризация кристаллов описывается первым членом в (14.3) и (14.4), в чем без труда можно убедиться, приравняв силу, действующую на электрон, нулю:

,

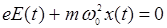откуда

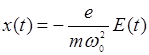(14.7)

и Р ~ Е, как и следует быть: поляризация пропорциональна мгновенному значению поля.

В несимметричном кристалле, как это легко видеть из выражения (14.6), положительное (х > 0) смещение электрона вызывает бόльшую возвращающую силу (при D > 0), чем отрицательное. Поэтому «отклик» среды на синусоидальное внешнее воздействие будет иметь вид искаженной синусоиды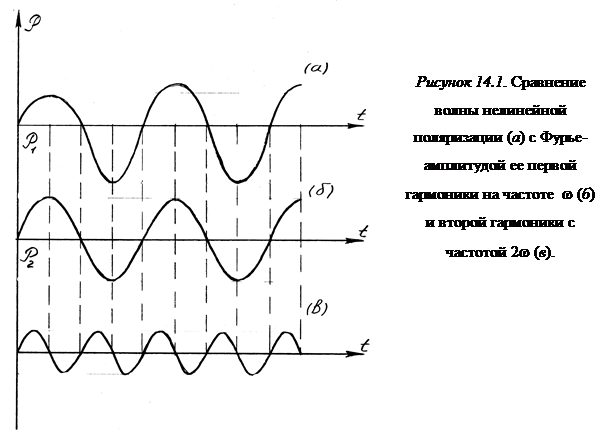
(см. рисунок 14.1)

Для количественного оформления этих соображений положим, что внешнее возмущение имеет вид

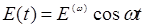
Тогда уравнение движения электрона в несимметричном кристалле будет иметь вид

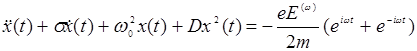(14.8)

Как видно, от классического уравнения затухающего осциллятора с внешней силой это уравнение отличается только «вредным» членом Dx²(t), описывающим колебания с частотой 2w. Член 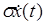описывает, как обычно, затухание. Решение x(t) будем искать в виде

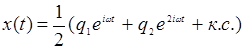(14.9)

Заметим, что в (14.8) и (14.9) необходимо сохранять действительную форму записи амплитуд, поскольку присутствует тот самый «вредный» член, содержащий x². Поэтому в дальнейшем придется везде таскать комплексно сопряженный «хвост», обозначаемый к.с. Это радикально отличает методику вычислений от линейного случая. Подставляя (14.9) в (14.8), получим:

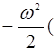
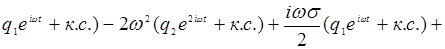
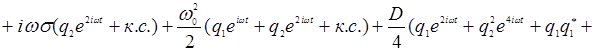
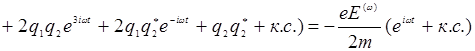(14.10)

Поскольку (14.10) должно быть справедливо для всех t, коэффициенты при

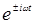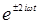и в обеих частях должны быть равны. Приравняем сначала коэффициенты при 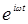, полагая, что 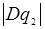<< 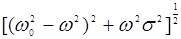. Получим:

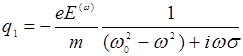(14.11)

Поляризация среды на частоте w связана с колебаниями электронов на той же частоте, как положено в классической электродинамике, формулой

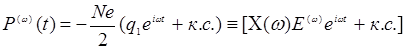(14.12)

Здесь C(w) – линейная диэлектрическая восприимчивость. Если подставить в (14.12) полученное согласно (14.11) выражение для q₁, то

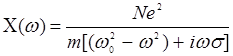(14.13)

Это известная из классики формула для диэлектрической восприимчивости. Теперь найдем желаемую амплитуду второй гармоники q₂ на частоте 2ω. Приравнивая коэффициенты при 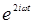в (14.10), получим с учетом (14.11):

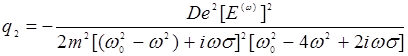(14.14)

Аналогично (14.12), запишем выражение для нелинейной поляризации на частоте 2ω:

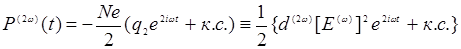(14.15)

Обозначим комплексную амплитуду поляризации Р^(2ω) . Тогда Р^(2ω) = = 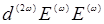. Таким образом, d^(2ω) – это отношение комплексной амплитуды поляризации к квадрату амплитуды поля на основной частоте. Согласно (14.14), имеем для d^(2ω):

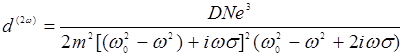(14.16)

Перепишем (14.16), введя нелинейную восприимчивость Χ^(2ω):

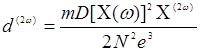(14.17)

Выражение (14.17) получено в предположении об изотропности среды. В действительности все кристаллы обладают анизотропией, т.е. связь между полем и поляризацией среды следует записывать не в виде 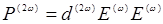, а в виде умножения вектора 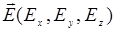на тензор 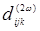, где каждая компонента вектора 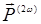запишется в виде:

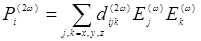(14.18)

Кристаллы, в зависимости от того, остается ли кристаллическая структура неизменной при инверсии, т.е. замене вектор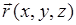а на 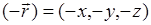, подразделяются на две группы: инверсионно-симмет-ричные и не обладающие таким свойством. В кристаллах, обладающих инверсионной симметрией, все нелинейные оптические коэффициенты 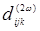должны быть равны нулю. Это следует из соотношения (14.18), если представить себе, что при изменении знаков у 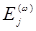и 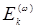изменившееся электрическое поле «видит» кристалл, идентичный первоначальному, т.е.

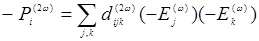(14.19)

Соотношения (14.18) и (14.19) могут одновременно выполняться только при 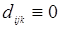. Это означает, что в кристаллах, обладающих инверсной симметрией, генерация второй гармоники невозможна.

Тензорная запись соотношения между полем и поляризацией безусловно необходима при конкретных расчетах и конструировании нелинейных умножителей оптической частоты. При этом приходится сталкиваться с довольно громоздкими вычислениями. Однако для оценок, позволяющих выяснить условия максимального коэффициента преобразования энергии из основной гармоники во вторую, тензорная запись не обязательна. Поэтому в дальнейшем ограничимся скалярной формой записи.

Разделим поляризацию на линейную (пропорциональную 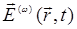) и нелинейную части:

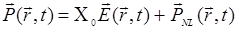
Полагая, что векторы 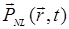и 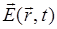параллельны, перейдем к скалярной форме записи волнового уравнения:

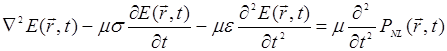(14.20)

Нетрудно видеть, что уравнение (14.20) выступает здесь как замена уравнения колебаний электрона (14.8), поскольку есть необходимость проследить за распространением волн с соответствующими частотами в конфигурационном пространстве кристалла, чего, разумеется, нельзя сделать, если рассматривать только колебания электрона вблизи выбранного положения равновесия. Представим поле 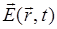как суперпозицию трех плоских волн с различными частотами ω₁, ω₂ и ω₃ , распространяющихся в направлении z :

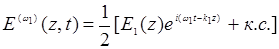
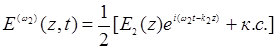(14.21)

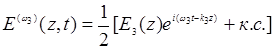
Мгновенное значение суммарного поля:

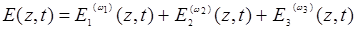(14.22)

Заметим, что представление (14.21)-(14.22) является более общим, чем это требуется для описания генерации второй гармоники, поскольку учитывает произвольные значения частот. Это значит, что аналогичным образом можно рассматривать и генерацию более высоких гармоник, а также нелинейные параметрические явления и резонансные нелинейные эффекты в изотропных средах.

Подставим (14.22) в волновое уравнение (14.20) с учетом (14.21). Тогда оно распадется на 3 уравнения, каждое из которых содержит только члены, описывающие колебания на одной из трех частот. Члены, содержащие 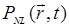, в соответствии с предположением об изотропности среды, имеют вид:

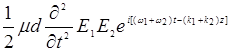
или

,

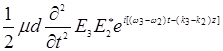т.е. содержат комбинационные частоты 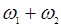и 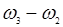. В случае несинхронности (произвольного соотношения частот) они не могут, вообще говоря, влиять на колебания на отдельно взятой частоте ω₁, ω₂ или ω₃. Но в случае 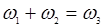член 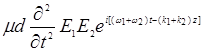может рассматриваться как источник волны на частоте 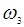. Физический смысл такого взаимодействия (появляющегося только при наличии члена P_NL) означает преобразование потоков энергии на частотах 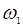и 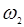в поток энергии на частоте 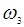и наоборот. В случае 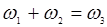волновое уравнение (14.20)для волны с частотой ω₁ запишется в виде:

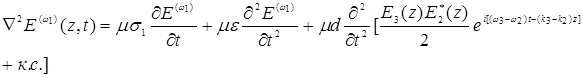
(14.23)

Преобразуем (14.23) к более простому виду, предполагая, что распространение волны 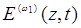вдоль оси z характеризуется медленным по сравнением с основной частотой изменением амплитуды: 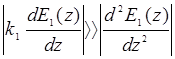, а также заменяя везде дифференцирование по времени умножением на соответствующий частотный множитель: 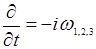. Учтем также, что

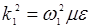. Получим:

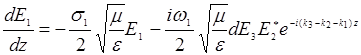(14.24)

Аналогичным образом получим уравнения для распространения волн с частотами ω₂ и ω₃ :

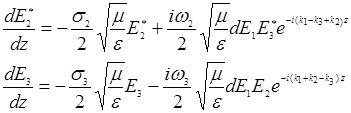(14.25)

Уравнения (14.24)-(14.25) имеют достаточно общий смысл и описывают нелинейные параметрические взаимодействия. Их легко обобщить и на анизотропный случай, вводя различные для разных волн значения диэлектрических постоянных ε₁, ε₂, ε₃ и вспоминая о тензорном характере нелинейных восприимчивостей d_ijk. Соответствующие расчеты проводились для многих кристаллов, и их результаты представлены в справочной литературе. Для простейшего случая генерации второй гармоники примем, что 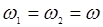. Тогда уравнения для Ε₁ и Ε₂ оказываются комплексно сопряженными, и достаточно рассматривать только Ε₁ и Ε₃ , имея в виду, что ω₃ = 2ω. Пренебрегая поглощением (σ_1,2,3 = 0), запишем (14.24)-(14.25) в виде:

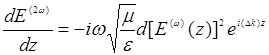(14.26)

где введено обозначение 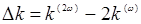. Допустим, что ослабление входной волны Е^(ω) из-за преобразования ее в волну Е^(2ω) незначительно. Пренебрежем поэтому зависимостью Е^(2ω) от z, а на входе волны с частотой 2ω еще нет (Е^(2ω) =0 ). Тогда интегрирование (14.26) в пределах оптической длины кристалла l дает:

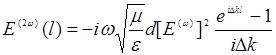
Отсюда найдем выходную интенсивность второй гармоники:

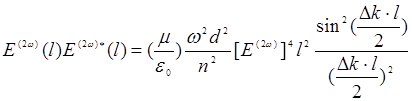(14.27)

В (14.27) введен показатель преломления: 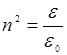. Пользуясь (14.27), можем найти светимость излучения второй гармоники (если ввести сечение выходного пучка А):

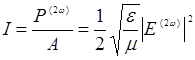(14.28)

и эффективность преобразования во вторую гармонику:

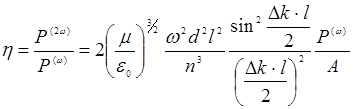(14.29)

Отсюда следует, что эффективность преобразования во вторую гармонику определяется продольным размером кристалла, интенсивностью входного пучка и, что особенно интересно, величиной Δk. Зависимость от Δk имеет интерференционный характер. Максимальная эффективность преобразования достигается при Δk = 0. Если Δk ≠ 0 , то имеет место интерференция волны второй гармоники самой с собой, т.е. энергия перекачивается от исходной волны во вторую гармонику и обратно. Два соседних максимума этой интерференционной картины удалены на расстояние 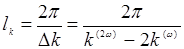, определяющее максимальную длину кристалла, при которой можно наблюдать излучение второй гармоники. Имея в виду, что 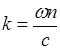, можно записать Δk в виде

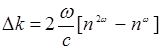(14.30)

откуда для длины когерентности l_k имеем:

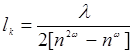(14.31)

Здесь λ — длина волны основного пучка в свободном пространстве. Если использовать произвольный кристалл, то, как правило, показатель преломления возрастает с частотой, и добиться выполнения условия 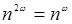невозможно. Поэтому в первых экспериментах по наблюдению второй гармоники излучения рубинового лазера использовались тонкие (~100 мкм) слои кристалла и очень большие интенсивности входного излучения. Коэффициент h в этих экспериментах (1961 г.) составлял 10^-11…10^-12. Между тем условие 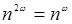выполнить вполне возможно, если воспользоваться двулучепреломляющим кристаллом, у которого волны с частотами w и 2w — разного типа (одна — обыкновенная, другая — необыкновенная). В качестве примера можно взять одноосный отрицательный кристалл. Зависимость показателя преломления необыкновенной волны от угла q между направлением распространения и оптической осью имеет вид

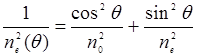(14.31)

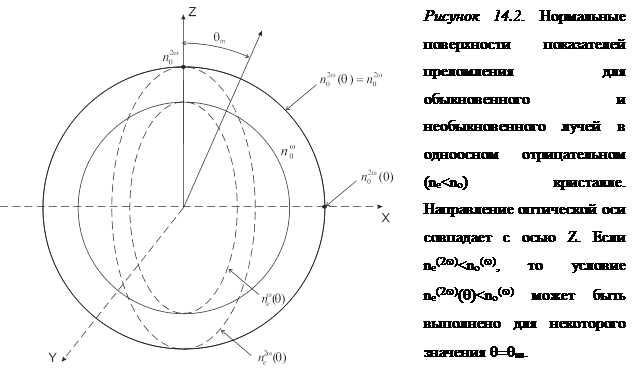Если n_e^2ω < n_o^ω , то существует угол θ_m , при котором 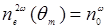. Таким образом, если основной пучок на частоте ω —это обыкновенная волна, распространяющаяся вдоль направления θ_m, то пучок второй гармоники будет распространяться вдоль того же направления θ_m как необыкновенная волна (рисунок 14.2).

Из (14.31) можно получить значение θ_m для данного одноосного отрицательного кристалла:

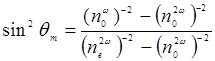(14.32)

Очевидно, что выполнение условия 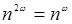очень критично к поляризации падающего излучения. Основной пучок в кристалле должен обладать поляризацией обыкновенной волны. Кроме того, можно указать другие причины малого коэффициента преобразования во 2-ю гармонику в экспериментах 1961 г.: работа в приближении плоской волны заставляет добиваться очень больших превышений над порогом генерации («тянуть» отношение 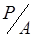до безумно больших величин). Отметим, что тогда теории гауссовых пучков еще не существовало. Остается только снять шляпу перед целеустремленностью группы Франкена (Franken P.A. et al.), все-таки сумевших зарегистрировать ультрафиолетовое излучение 2-й гармоники рубинового лазера и опубликовавших скромное сообщение всего лишь из одной страницы
в «Phys. Rev. Letters», положившее начало нелинейной оптике.

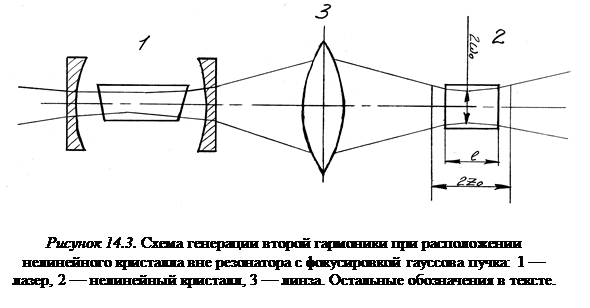
Значительно целесообразнее работать с фокусировкой входного пучка. (см. рисунок 14.3)

В самом деле, допустим, что лазер, работающий на основной гармонике, излучает гауссов пучок с конфокальным параметром 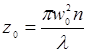(n – показатель преломления активной среды в резонаторе). Если 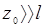(l – оптическая длина преобразующего кристалла), то внутри кристалла поперечное сечение пучка можно считать постоянным.

Напомним, что физический смысл параметра z_o есть расстояние от перетяжки пучка до плоскости, где сечение пучка в 2 раза больше, чем в перетяжке. Считая, что z » l, запишем:

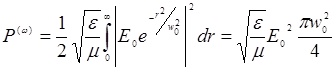
Тогда вместо (14.29) для эффективности преобразования можно записать:

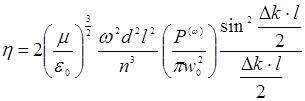(14.33)

Здесь .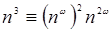

Согласно (14.33), выходная мощность во 2-й гармонике может быть увеличена за счет уменьшения перетяжки w_о. Это возможно до тех пор, пока z_о не станет сравнимой с l. В случае, когда 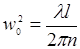(конфокальная фокусировка), дальнейшее увеличение η уже невозможно. Поэтому довольно быстро стал применяться более радикальный способ увеличения η — помещение нелинейного кристалла внутрь резонатора. В самом деле, внутри резонатора плотность мощности в 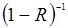раз больше, чем снаружи. При R ~ 1 эта величина может быть сделана очень большой.

Рассмотрим для примера резонатор, в котором при данной скорости накачки максимальная выходная мощность достигается при оптимальном пропускании зеркала (полагая, что превышение не очень велико, что реализуемо в случае лазера на АИГ:Nd). Заменим выходное зеркало глухим (100% отражения) по отношению к излучению частоты ω, а в резонатор поместим нелинейный кристалл (рисунок 14.4).

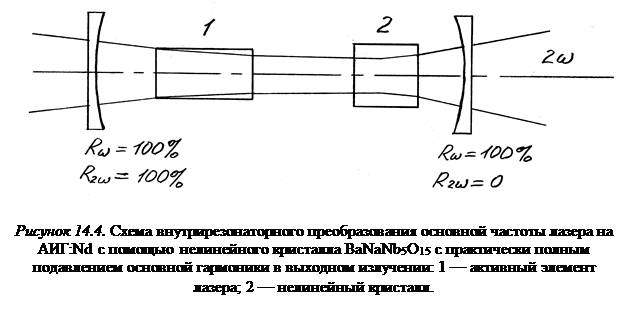
Величина оптимального пропускания (см. Л3, Л12) при небольших превышениях дается формулой

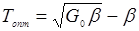(14.34)

где G_o – ненасыщенный однопроходный показатель усиления, β – распределенные однопроходные потери. Выходная мощность в этом случае равна

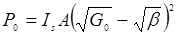(14.35)

где Ι_s - интенсивность насыщения (см. Л3). В силу предположения о полном преобразовании выходной энергии во 2-ю гармонику будем считать, что потери на зеркале полностью совпадают с коэффициентом преобразования:

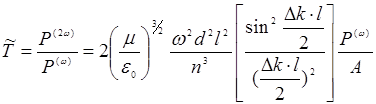(14.36)

Обозначим в (14.36) множитель при Р^(ω) как :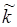

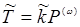(14.37)

Подставляя (14.37) в (14.34), видим, что оптимальное преобразование во вторую гармонику имеет место, если

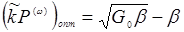(14.38)

Суммарные однопроходные потери для основного излучения:

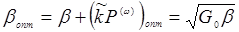
Заменяя в (14.35) выражение для β его оптимальным значением, получим:

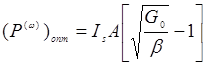(14.39)

Соответственно для второй гармоники:

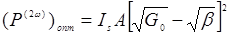(14.40)

Из (14.37) и (14.40) можно выразить постоянную нелинейной связи 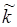в оптимальном случае:

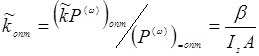(14.41)

Заметим, что 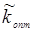не зависит от накачки (в (14.41) не входит ненасыщенный показатель усиления G_o ). Поскольку 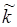зависит не только от l, d и А , но и от фазового рассогласования Δk·l (т.е. от направления распространения волны относительно оптической оси кристалла), можно менять 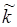, изменяя ориентацию кристалла в резонаторе. Условие Δk = 0 называется условием фазового синхронизма. Его выполнение является основной задачей при юстировке лазера с нелинейным преобразованием частоты.

Проведенное рассмотрение внутрирезонаторного преобразования предполагает, что потери на выходном зеркале полностью совпадают с коэффициентом преобразования. К сожалению, в случае АИГ:Nd-лазера (весьма распространенного в медицинских применениях) возникает осложняющее обстоятельство, связанное с тем, что у кристалла АИГ:Nd имеется сильная линия поглощения, совпадающая с длиной волны второй гармоники. Поэтому значительная часть излучения последней, отраженной от выходного зеркала, будет поглощаться в активном элементе. Если поставить между нелинейным кристаллом и активным элементом дополнительное зеркало, пропускающее основную частоту и полностью отражающее вторую гармонику, то возникает интерференция волн, распространяющихся направо и налево. В зависимости от соотношения фаз эти составляющие могут либо суммироваться, либо гасить друг друга. Разность фаз будет зависеть от изменения расстояния между зеркалами, расположенными рядом с нелинейным кристаллом. Это резко усложняет настройку и юстировку лазера и ухудшает стабильность его работы. Кроме того, увеличивается вероятность пробоя нелинейного кристалла.

Проблема снимается, если преобразование осуществлять в резонаторе кольцевого лазера, работающего в режиме бегущей волны. Возможная схема представлена на рисунке 14.5.