Составляющие силы тяжести

Остановимся коротко на основных слагаемых силы тяжести 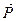. Это, прежде всего, нютонианская сила притяжения

F_пр=G 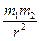(1)

Это всем известное выражение, называемое законом всемирного тяготения Ньютона читается так: две материальные точки в вакууме притягиваются друг другом с силой прямо пропорциональной произведению их масс и обратно пропорционально квадрату расстояния между ними. Как и всякий идеальный закон, он приложим только к идеальной практике, к закрытым системам: вакуум, материальные точки и пр. Такое достижимо только в условиях лабораторного эксперимента, когда можно откачать воздух, свести действующую массу в точку и пр. Для адаптации закона к реальности, к открытым системам необходимо сделать некоторые существенные допущения, например, считать размеры взаимодействующих масс пренебрежимо малыми в сравнении с расстояниями их взаимодействия, а сами массы концентрически однородными. Для характеризации взаимодействия планет этого будет вполне достаточно. Но для употребления закона Ньютона, для объяснения притяжения измерительного элемента прибора-гравиметра неоднородностями земной коры или Землей в целом, которую трудно принять за однородное тело, он не годится. Приходится дробить неоднородности на бесконечно малые кусочки, в пределах которых можно считать плотность постоянной (то есть использовать дифференциальный подход), затем оценивать по приведенной формуле притяжение измерительного элемента прибора каждым таким кусочком и, наконец, суммировать притяжение этих кусочков, интегрируя по всему замкнутому контуру, по всему объему, занимаемому данной массой – плотностной неоднородностью земной коры или Землей в целом.

Идею прибора гравиметра можно представить себе следующим образом: штатив (1), пружинка (2) и грузик (3).

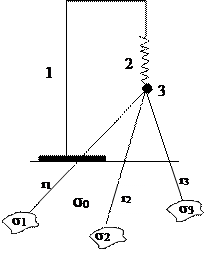Рис.2.К измерению силы притяжения.

Если поместить такую простую установку на поверхность Земли, грузик будет испытывать притяжение со стороны всех масс-неоднородностей разреза m₁,m₂ и m₃ применительно к ситуации, изображенной на рис.2. То есть все эти массы одновременно повлияют на растяжение пружины 2 грузиком 3 и прибор будет регистрировать суммарное их притяжение. Каждая масса даст в это суммарное притяжение вклад, пропорциональный своей массе, которая равна произведению занимаемого ею объема на эффективную плотность, и обратно пропорциональный квадрату удаления этой массы от измерительного элемента прибора (грузика), находящегося на поверхности Земли. Эффективная плотность σ_эф1 есть разность плотностей «возмущающего» тела σ₁ и вмещающей среды σ₀; σ_{эф2 =} σ₂ - σ₀ и σ_{эф3 =} σ₃ - σ₀.

Таким образом, каждая неоднородность дает в регистрируемую суммарную величину F_пр вклад тем больший, чем больше его объем, и контрастность плотности σ_эф и чем меньше глубина его залегания. В итоге регистрируемая при перемещении прибора вдоль линии профиля наблюдений кривая F_пр может иметь достаточно сложный рельеф, который не всегда очевидно увязывается с картиной распределения источника F_пр . Так, на рис.3 в рельефе кривой виден только один суммарный максимум притяжения, в то время, как источником этого максимума являются не одна, а две неоднородности разреза.

Рис.3. К иллюстрации суммарного характера кривой ∆g.

Но вернемся к записи (1) закона тяготения. Здесь представляет интерес коэффициент G, называемый гравитационной постоянной. По своему физическому смыслу G – это сила, действующая между двумя единичными массами m₁ и m₂, удаленными друг от друга на расстоянии, равном единице длины. То есть, если поместить две сосредоточенные (точечные) массы, каждая из которых равна единице (1 кг) на расстоянии, равном 1 метру, то сила взаимодействия между ними будет равна не единице, а составит 66,7·10^-12. Размерность G 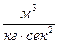. Откуда взялась эта константа, какова ее природа не совсем понятно. Ясно только, исходя из концепции происхождения и становления Вселенной, именуемой концепцией Большого взрыва, что в процессе расширения Вселенной в период от 10^-35 до 10^-33 секунды происходит фазовый переход, в процессе которого вакуумное состояние посредством туннельного эффекта превращается в горячую плотную Вселенную [10]. Вселенная при этом распадается на отдельные области, одна из которых приобретает свойства четырехмерного пространства – времени. В таком переходе вследствие спонтанного нарушения симметрии единое взаимодействие расчленяется и гравитация отделяется от трех остальных взаимодействий. Тем самым силы гравитации определяют формирование Вселенной буквально с момента ее зарождения, а константа Ğ становится одной из четырех основных мировых констант (остальные три – это постоянные Больцмана, Планка и скорость света), на пересечении которых стоит современный мир и существует человек (антропный принцип). Формулировка антропного принципа, связанного с происхождением Вселенной, как раз и состоит в том, что сложность наблюдаемой Вселенной определяется очень узким диапазоном сечений первичных элементарных процессов и значениями фундаментальных констант. «Если бы сечения элементарных процессов в эпоху Большого взрыва были бы, скажем, немного больше, то вся Вселенная «выгорела» бы за короткий промежуток времени» [10]. Все это дает основания некоторым мыслителям считать, что в этих физических константах и, в частности, в гравитационной, заключается доказательство присутствия Господа Бога на Земле и его замысла о человеке, о предназначении человечества.

Если в адаптированном законе Ньютона положить одну из масс m₁ равной единице, а вторую m₂ обозначить просто m, то можно записать этот закон в виде F=G 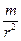·1 = j и тогда F будет иметь смысл напряженности, то есть силы, отнесенной к единице массы. Если еще раз переписать закон с учетом j, получим запись F=mj, аналогичную таковой для второго закона Ньютона F=ma, где а – ускорение, испытываемое массой m под действием силы F. И, тем самым, убедимся, что напряженность поля притяжения имеет смысл ускорения. Заметим, что F_пр будет зависеть от широты φ точки местности, где находится притягиваемая масса m. Поскольку экваториальный радиус r_э больше r_п - полюсного, F_пр достигает максимального значения на полюсе и постепенно уменьшается в направлении экватора. Ускорение, как уже говорилось, векторная величина. Скалярные составляющие j (F_пр ) по координатным осям обозначены F_прx , F_прy и F_прz соответственно. Чтобы оценить притяжение m земным сфероидом, его необходимо разбить на точечные массы, то есть массы бесконечно малых размеров dΩ. В результате притяжение сфероида будет определяться, как уже говорилось выше в отношении силы тяжести, интегральной сумме притяжений каждой из находящихся внутри него точечных масс. Однако суммировать их арифметически нельзя, поскольку направления действия этих элементарных сил притяжения разными точечными массами окажутся различными и такое суммирование можно выполнять только раздельно для указанных составляющих по осям x,y,z.

Тогда полное значение силы притяжения массы m в точке, где эта масса находится, составит

F_пр=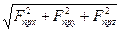

Второе слагаемое силы тяжести Р – центробежная сила F_ц. Она определяется суточным вращением Земли вокруг своей оси. Это сила, с которой тело, находящееся под ее действием, стремится улететь от Земли и величина ее определяется угловой скоростью и радиусом вращения. Направлена эта сила по перпендикуляру ρ к оси вращения.

Таким образом, F_ц= ω² ·ρ·m, где ρ – радиус вращения, ω – угловая скорость, равная v/ρ; v – линейная скорость.

Из этого выражения видно, что на полюсе, где ρ=0, центробежная сила также равна нулю, а максимальное ее значение фиксируется там, где максимума достигает радиус вращения ρ, то есть на экваторе.

Составляющих F_ц по координатным осям будет только две - F_цx и F_цу , тогда как F_цz окажется равной 0, поскольку проекция F_ц на ось Z падает в точку, так как F_ц ┴ Z. Таким образом, получается, что F_ц не зависит от распределения масс внутри Земли, то есть не участвует в создании аномалии Δg , измеряемой на поверхности Земли, но как мы увидим далее, она учитывается в нормальном поле.

Гравитационный потенциал

Теперь целесообразно ввести в рассмотрение функцию, называемую гравитационным потенциалом. Напомним, что под потенциалом понимается работа сил поля по перемещению единичной массы из бесконечности в данную точку пространства. Таким образом, потенциал представляет собой меру энергии и выражается в джоулях. Исходя из данного определения, максимальное значение гравитационного потенциала может быть зарегистрировано в центре Земли. Однако, нас интересует в рассматриваемом контексте не столько физический смысл потенциала, сколько его чисто математическая сущность. Дело в том, что от рассмотрения векторов F удобно для характеризации поля перейти к скалярному его описанию. В качестве скалярной функции, через которую определено поле силы тяжести принимается гравитационный потенциал W.

Аналитически потенциал определяется как функция, частные производные которой по координатным осям X,Y и Z соответственно равны составляющим силы тяжести

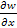=g_x= g 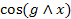; 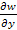=g_y= g 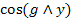; 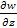=g_z = g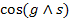

И в общем случае, то есть в произвольном направлении S 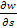=g_s= g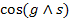

То есть частные производные потенциала - это проекции силы тяжести на оси координат X, Y и Z или на линию (поверхность) S, по которой перемещается действующая масса m. Вполне понятно, что гравитационный потенциал W является суммой потенциалов притяжения V и центробежной силы U, поскольку сама сила тяжести Р есть векторная сумма силы тяжести ньютонианского притяжения F и центробежной силы F_ц

то есть W = V + U, где V = G 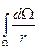; _{U =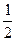} (x²ω² + y²ω²)

Дифференцируя эти выражения по X,Y и Z нетрудно получить соответствующие выражения для g_x , g_y, и g_z , а также для F_пx, F_пy и F_пz, F_цx и F_цy , а также убедиться, что F_цz =0, поскольку приведенное выражение для потенциала центробежной силы U не содержит Z. Таким образом, каждой точке пространства соответствует непрерывная, имеющая непрерывные производные скалярная функция W, производные которой по X, Y и Z являются проекциями силы на соответствующие оси координат.

Важно заметить, что вертикальная составляющая g_z, учитывая, что F_цz = 0 является частной производной по Z от потенциала притяжения, то есть

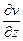g_z = =V_z.

Важнейшее свойство потенциала.

Зададимся вопросом: как выглядит распределение потенциала на поверхности, в любой точке которой g направлено по нормали к этой поверхности, то есть S 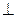g. В этом случае cos(g,s)=0 и, соответственно, 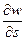= 0, а W=const (W =C). Такая поверхность, в любой точке которой сила тяжести (притяжения) направлена к ней нормально, а потенциал W(U) имеет постоянное значение, называется поверхностью равного потенциала или уровенной поверхностью. На такую поверхность действует только нормальная (вертикальная) составляющая g (то есть g_z). На такой поверхности устанавливается – не течет – жидкость в сосуде (если пренебречь силой поверхностного натяжения).

Из всего мыслимого множества уровенных поверхностей, отвечающих уравнению W=C (C₁,C₂,C₃ –различные значения постоянной соответствуют различным уровенным поверхностям) есть одна, которая существует физически, которую можно потрогать. Это поверхность невозмущенной никакими горизонтальными (тангенциальными) силами (например, силы ветра) морей и океанов. Будучи мысленно продолженной под континенты она обрисует фигуру Земли, которую называют геоид. Именно геоид принимают за фигуру Земли в геологии, во всех геологических науках, кроме гравиразведки. В гравиразведке, как уже говорилось выше, за фигуру Земли, за ее модель принимают сфероид. Чем они отличаются? Геоид – это эквипотенциальная поверхность реальной вращающейся Земли, тогда как сфероид – эквипотенциальная поверхность воображаемой (модель) вращающейся Земли, у которой все горы выровнены, а моря заполнены на одинаковую глубину. При этом ее масса и объем остаются такими же, как у реальной Земли. [4 ]. Почему же гравиметристов не устраивает в качестве модели геоид, а устраивает только сфероид?

Дело в том, что геоид это поверхность не идеальная, а ундулирующая. Ундуляции или местные возмущения возникают под действием физических неоднородностей земной коры и топорельефа местности. На рис.4 видно, что из-за притяжения «избытков» масс (например, горных массивов краевых зон континентов) отвес отклоняется в сторону этих масс, а показанная пунктиром уровенная поверхность (всегда перпендикулярная вектору g, который как раз и определяет нить отвеса) образует, таким образом «положительную» ундуляцию (вздымается). Над океаном из-за недостатка масс образуется отрицательная ундуляция.

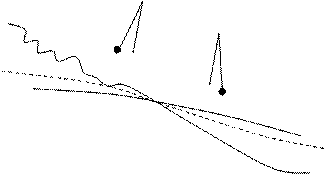
Рис.4.Ундуляции геоида.

Срезающая эти ундуляции на рис.4 сплошная кривая дает представление об осредненном невозмущенном положении геоида. Такой геоид называют эллипсоидом относимости. Трехосный эллипсоид - это более близкое, чем сфероид приближение к истинной фигуре Земли, поскольку у нашей планеты различаются не только полюсной и экваториальный радиусы. Если рассмотреть само экваториальное сечение, то оно на самом деле окажется не идеальным кругом. Два главных радиуса этого сечения буду различаться примерно на 200 м. В сравнении с различием полюсного и экваториального радиусов, разница между которыми составляет ~21 км, это всего лишь 1%, и тем не менее, эллипсоид – это более точное представление фигуры Земли. Поэтому в большой геофизике именно эллипсоид определяет эту фигуру, но для гравиразведки вполне годится в качестве модели сфероид. Сфероид – это поверхность практически идеальная, близкая к среднему невозмущенному положению геоида и для такой поверхности нетрудно вычислить нормальное поле Δg₀, которое необходимо для получения имеющих геологический смысл аномальных значений Δg_а. В целом поверхность земного сфероида незначительно отклоняется от поверхности геоида на морях и океанах – в среднем на ±50м.

Градиенты силы тяжести

Сама по себе величина потенциала W непосредственно не измеряется. Измерению подлежат только первые производные W_z, то есть составляющие g, в частности g_(z) и вторые производные потенциала W_zx и W_zy, именуемые градиентами силы тяжести

W_zx= 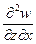= = 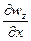dg /dx

W_zy= = =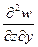

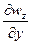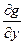
Вторые производные W_zx и W_zy характеризуют скорость изменения g_z (то есть ее градиент) по горизонтали (в плоскости xoy, касательной к поверхности) и имеют размерность 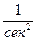. Их называют горизонтальными градиентами силы тяжести, в отличие от вертикального W_zz= 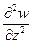= = 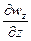dg /dz. Именно горизонтальные градиенты имеют геологический смысл, поскольку над относительно небольшими телами, зачастую почти не проявляющими себя в поле Δg_а, наблюдаются аномалии W_zx и W_zy.

Вертикальный градиент позволяет оценить, как меняется сила тяжести с изменением высоты точки наблюдения относительного уровня моря, то есть поверхности сфероида (геоида). Из всех градиентов вертикальный имеет наибольшую величину, которая составляет примерно 3·10^-6 1/с².

За единицу измерения градиентов силы тяжести принимается этвеш (Е). Один Е соответствует изменению силы тяжести на 0,1 мГал на участке в 1 км. Таким образом

1 Е=10^-91/сек².

Название этвеш связано с именем венгерского физика Этвеша, который изобрел специальный прибор для измерения градиентов – гравитационный вариометр, действующий по принципу крутильных весов Кулона. В наше время вариометрические съемки проводятся сравнительно редко, в основном в рудной геофизике

.