Взаимное положение плоскостей в пространстве

Две плоскости в пространстве могут быть либо взаимно параллель-ными, либо пересекающимися.

Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Пересекающиеся плоскости. Линией пересечения двух плоскостей является прямая, для построения которой достаточно определить две точки общие обеим плоскостям.

Рассмотрим решение задачи на построение линии пересечения двух плоскостей: ∆ABC и ∆DEF (рис. 29). Точки M и N, определяющие искомую линию пересечения двух данных плоскостей найдем как точки пересечения каких-либо двух сторон (как две прямые) треугольника ABC с плоскостью другого треугольника DEF, т.е. дважды решим позиционную задачу на определение точки пересечения прямой с плоскостью.

Рис. 29 Определение линии пересечения двух плоскостей

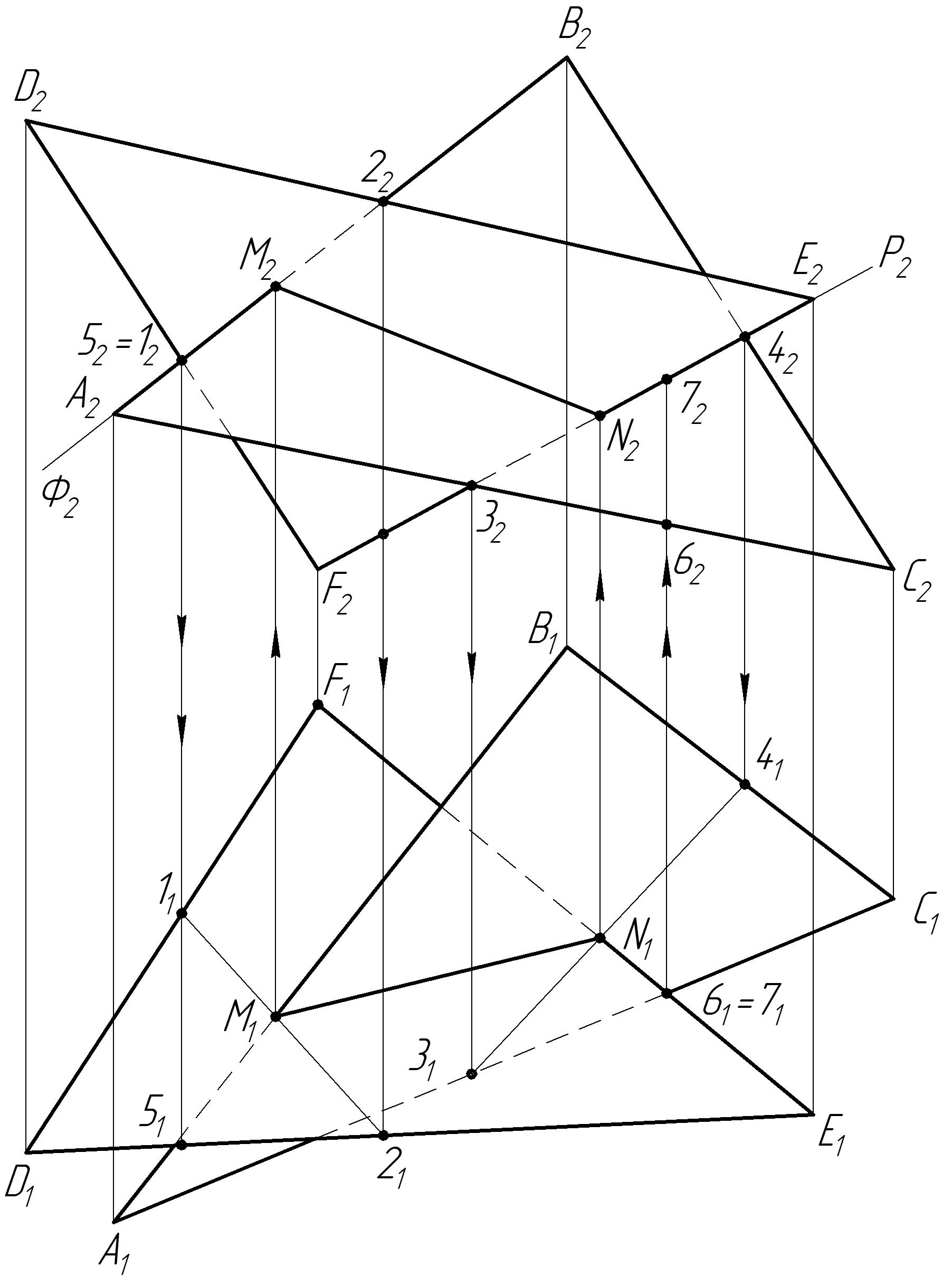
Выбор сторон треугольников произволен, так как только построением можно точно определить, какая действительно сторона и какого треугольника пересечет плоскость другого. Выбор вспомогательной плоскости также произволен, так как прямую общего положения, какими являются все стороны ∆ABC и ∆DEF, можно заключить в горизонтально проецирующую или во фронтально проецирующую плоскости.

1. Для построения точки M использована горизонтально проецирующая вспомогательная плоскость Ф (Ф₂), в которую заключена сторона AB треугольника ABC (AB Î Ф).

2. Строим линию пересечения (на чертеже она задана точками 1 и 2) вспомогательной плоскости Ф (Ф₂) и плоскости ∆DEF.

3. Находим точку M пересечения прямой 1–2 с прямой AB.

Найдена одна точка M искомой линии пересечения.

4. Для построения точки N использована горизонтально проецирующая плоскость Р (Р₂), в которую заключена сторона EF треугольника DEF.

Построение аналогичны предыдущим.

5. Определение видимости элементов на плоскости П₂ выполнено с помощью фронтально конкурирующих точек 1=2 и 5=2.

Точка 5 (5ÎАВ) расположена дальше от оси х чем точка 1 (1Î DF), поэтому на плоскости П₂ часть треугольника ABC, расположенная в сторону точки 1, закрывает собой часть треугольника DEF, расположенную от линии пересечения в сторону точки 5.

С помощью пары горизонтально конкурирующих точек 6=1 и 7=1 определена видимость на плоскости П₁.