Динамические характеристики объекта управления

Как уже отмечалось ранее, переходным процессом называется переход системы из одного установившегося состояния в другое установившееся состояние. Зависимость изменения величины выходных параметров системы за время переходного процесса в зависимости от изменения входных параметров или внешнего возмущения называется динамической характеристикой системы.

При исследовании системы или ее элементарных звеньев чаще всего рассматривается реакция системы на единичное ступенчатое воздействие или на единичную импульсную функцию. Данная реакция системы является типичной при реальном воздействии, т.е. реальное воздействие можно разложить на сумму единичных воздействий. Графическое представление этих воздействий изображено на рисунке 24.

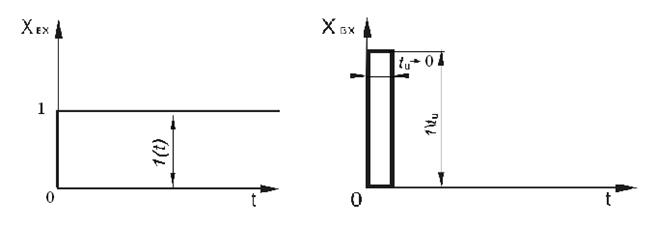
Рис. 24. Единичное ступенчатое и единичное импульсное воздействия

Единичную функцию принято обозначать 1(t), математически ее можно представить в виде:

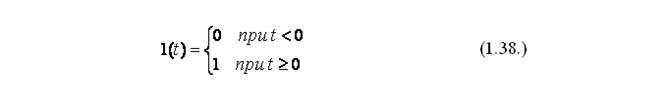
Переходной функциейh(t) называется реакция системы или звена (изменение во времени выходного параметра y(t), в ответ на входное единичное ступенчатое воздействие при нулевых начальных условиях. К такому виду воздействия или внешнего возмущения относят мгновенное изменение задания автоматическому регулятору, мгновенное возрастание нагрузки на валу электродвигателя.

Единичной импульсной функцией принято считать импульс, площадь которого равна единице, математически она представлена:

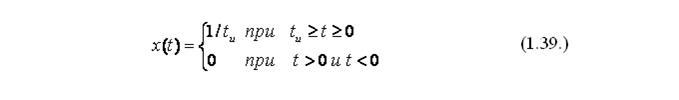
При t_и = 0 единичная импульсная функция превращается в некоторую функцию, используемую чаще всего и называемую дельта-функцией б(t), значение которой равно нулю при всех значениях t, кроме t = 0, когда оно равняется бесконечности, ее математическое представление:

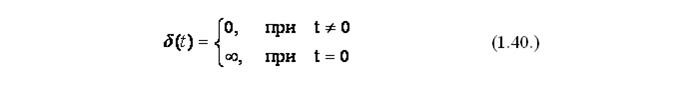Единичная дельта - функция б(t) (единичный импульс) представляет собой математическую идеализацию импульса бесконечно малой длительности, бесконечно большой амплитуды, имеющего конечную площадь, равную единице, т.е.:

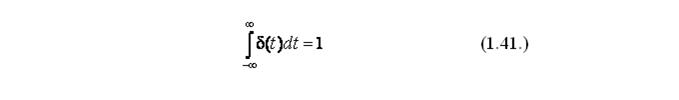
Существует связь между дельта-функцией б(t) и единичной ступенчатой функцией 1(t), которая выражается следующим образом:

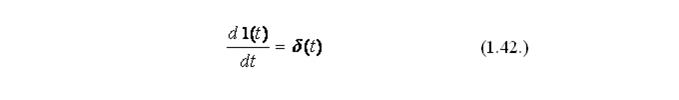
Весовой функциейw(t) или импульсной переходной функцией называется реакция звена или системы на входное воздействие в виде дельта-функции при нулевых начальных условиях, поэтому переходная h(t) и импульсная переходная w(t) функции могут быть сравнительно просто преобразованы одна в другую т.е. верно равенство:

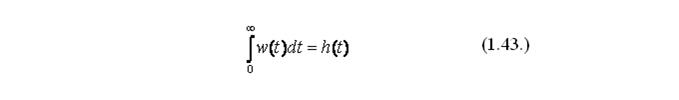
Весовая функция w(t) системы связана преобразованием Лапласа с ее передаточной функцией, т.е. если x(t) = б(t), то X(р) = 1. В соответствии с таблицей преобразования (рисунок 23), y(t) = w(t), и согласно определению передаточной функции:

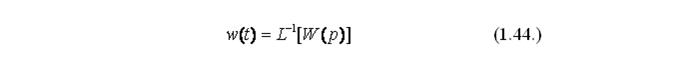
Применив прямое преобразование Лапласа к предыдущему выражению, получаем,

что передаточная функция является изображением весовой функции и связана с ней интегральным преобразованием Лапласа:

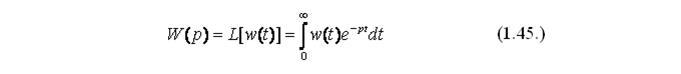
Передаточная функция системы W(р) также связана с переходной функцией системы h(t). Пусть x(t) = 1(t), тогда X(р)=1 / p, и в соответствии с таблицей преобразования y(t) = h(t). В соответствии с определением передаточной функции получаем:

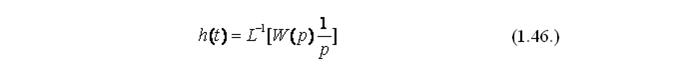
Применив к предыдущему выражению прямое преобразование Лапласа, получим:

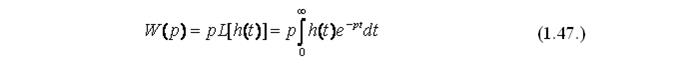
Следовательно, применяя типовые воздействия, можно описать реакцию системы в переходном режиме на произвольное изменение величины входного параметра х(t). Такое возможно только для случаев описания процессов в линейных системах, для которых справедлив принцип суперпозиции. Принцип суперпозиции заключается в том, что реакция линейной системы на сумму входных воздействий, равна сумме реакций на каждое воздействие.

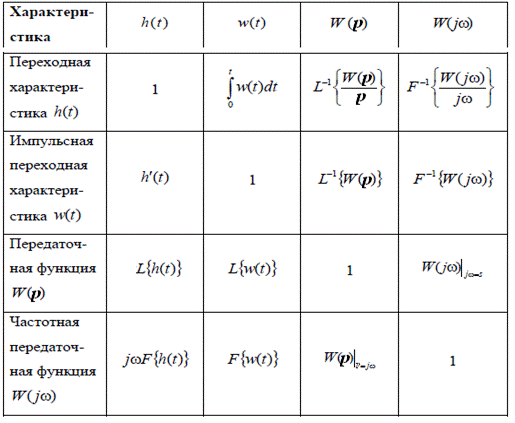
Рис.24.1. Взаимосвязь характеристик САУ между собой и передаточной

функцией

Любое входное воздействие мы можем представить в виде суммы единичных ступенчатых или импульсных воздействий, поэтому существует возможность для определения реакции системы на произвольное возмущение, зная ее реакцию на типовое воздействие. Момент приложения внешних воздействий к системе обычно принима­ется за нуль отсчёта времени, поэтому в математические выражения для внешних воздействий в ка­честве множителя вводят единичную ступенчатую функцию.

На рисунке 24.1. представлена таблица, в которой указана взаимосвязь характеристик систем автоматического управления между собой и передаточной функцией.

Сложное внешнее воздействие приближен­но представляется в виде некоторого количества типовых воздействий, которые свя­заны между собой математическими операциями.

Решив дифференциальное уравнение, описывающее динамику системы, можно найти реакцию системы на типовое или любое другое воздействие. Например, решив дифференциальное уравнение при нулевых начальных условиях и x(t)= 1(t) можно найти переходную функцию системы h(t).

Используя переходную функцию h(t) можно определить реакцию системы (выходной параметр) на некоторое воздействие, не решая дифференциального уравнения. При х(0)= х(t), t = 0, получим следующее выражение, описывающее реакцию системы:

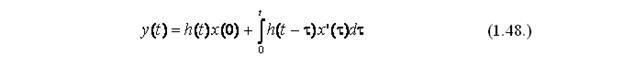
где t – вспомогательная переменная интегрирования. Реакцию системы y(t) на некоторое входное воздействие x(t) можно вычислить, как предел суммы реакций на единичные ступенчатые воздействия высотой Dx(t+Dt), на которые можно разложить x(t), при Dt стремящегося к 0.