Математическое описание объектов управления.

При исследовании и проектировании систем автоматического управления возникает необходимость описания процессов происходящих в самой системе и в ее отдельных звеньях. Чаще всего для этого применяется математическое описание процесса, называемое математической моделью САУ, представляющее собой совокупность ограничивающих критериев, допущений, и уравнений, описывающих законы изменения выходных параметров от входных, в переходном и установившемся режимах. Уравнение, описывающее изменение во времени выходного параметра системы в зависимости от входного параметра, называется уравнением динамики. Им определяется динамический режим системы или звена, возникающий при воздействии возмущений.

Понятия установившегося и переходного (неустановившегося) режимов проиллюстрированы графиками возможных изменений управляемой величины y(t) при

типовых воздействиях для систем автоматического управления на рисунке 22.3.

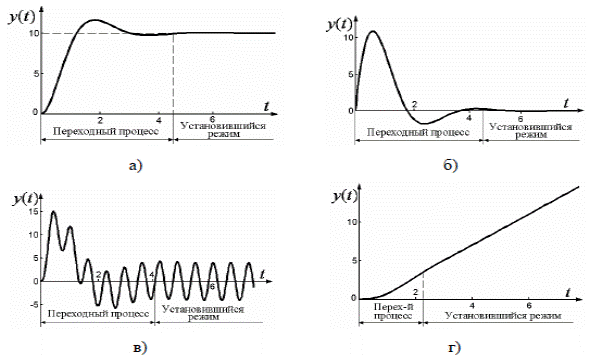
Рис.22.3. Реакции САУ на типовые воздействия

а) сигнал x(t) =1(t); б) сигнал x(t) =δ (t) ;

в) сигнал x(t ) = 1(t )10sin(10t ) ; г) сигнал x(t ) = 1(t )0, 2t

Переходным процессом называется состояние системы в момент ее перехода из одного установившегося режима в другой установившийся режим, при изменении задающих параметров, влиянии внешнего возмущения. Чаще всего для более полного описания переходных процессов системы используются дифференциальные или интегрально-дифференциальные уравнения, процессы в отдельных звеньях могут описываться алгебраическими уравнениями. Одна и та же система, в зависимости от цели исследования, может описываться различными способами.

Системы в установившихся режимах описываются в виде состояния покоя, равновесия, или, как движение системы с постоянной скоростью, и описываются уравнениями статики. Уравнение статики, описывающее установившийся режим, является дифференциальным уравнением нулевого порядка, которое можно преобразовать в

алгебраическое. Уравнения динамики, как и уравнения статики, подразделяются на линейные и нелинейные. Линейные дифференциальные уравнения являются наиболее простыми для практического применения, нелинейные уравнения рассчитывать намного сложнее. Для удобства расчетов применяют линеаризацию.

Линеаризация – процесс приведения криволинейных статических характеристик звеньев, используемых в процессе управления к прямолинейным характеристикам. Самым распространенным методом, используемым в процессе линеаризации, является метод малых отклонений, который допускает, что отклонения входных и выходных параметров системы в процессе управления от их установившихся значений достаточно малы. В основе метода линеаризации лежит разложение в ряд Тейлора, которое позволяет разложить нелинейную функцию нескольких переменных по степеням малых отклонений этих переменных в окрестностях значений, соответствующих заданному установившемуся режиму.

Дифференциальные уравнения звеньев системы составляются соответственно закономерностям протекающих в них физических процессов. При регулировании давления, уровня, используется закон сохранения вещества, при регулировании химической реакции- закон действующих масс, при регулировании температуры – закон сохранения энергии, также используются законы Ома, законы Кирхгофа и т.д. Для составления уравнения необходимо сначала определить процесс, который протекает в исследуемом звене, математическое описание закона соответствующего данному процессу и будет являться исходным дифференциальным уравнением динамики звена.

Составляя дифференциальные уравнения систем, данные системы расчленяют на ряд простых звеньев, для каждого звена составляют уравнения статики и динамики, причем величина выходного параметра предыдущих звеньев является входной величиной последующих. Далее, исключая промежуточные переменные, получают модель системы в целом.

Переменные в математических моделях систем могут представляться в переменных «вход-выход» или в переменных состояния. При представлении в переменных «вход-выход» для описания моделей используются дифференциальные уравнения произвольного порядка, при описании в переменных состояния – уравнения Коши.

Уравнения Коши – система дифференциальных уравнений первого порядка, разрешенных относительно первых производных, которые также называются уравнениями состояния.

В общем виде уравнение для линейной стационарной САУ является линейным неоднородным дифференциальным уравнением, представленное подобным образом:

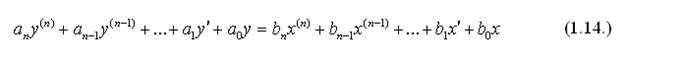
где у и х – входные и выходные величины, а и b – коэффициенты, определяемые параметрами системы, n – порядок уравнения.

Линейные дифференциальные уравнения, применяемые для описания процессов в звеньях и системах автоматического управления, могут быть решены с помощью классического метода или с помощью преобразования Лапласа.

Решение уравнения классическим методом, где определяется изменение выходного параметра в зависимости от времени, при заданном входном параметре и известных начальных условиях, представляется в следующем виде.

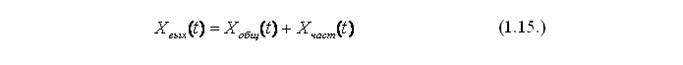
где Х_вых(t) – изменение выходного параметра, Х_общ(t) – общее решение однородного дифференциального уравнения, Х_част(t) – частное решение неоднородного дифференциального уравнения.

Характер изменения входного параметра не влияет на общее решение уравнения и определяется параметрами системы, поэтому общее решение однородного дифференциального уравнения Х_общ(t) определяет переходной процесс в системе и называется свободной (переходной) составляющей.

Частное решение неоднородного дифференциального уравнения Х_част(t) является вынужденной составляющей, характеризующей установившийся процесс в системе, т.к. данное решение зависит и от параметров системы, и от характера изменения входного параметра.

Очень сложную задачу представляет применение классического метода при решении дифференциальных уравнений высокого порядка, поэтому на практике обычно применяется интегральное преобразование Лапласа.