Тема №8. Переходные процессы в линейных электрических цепях.

Введение.

Рассматриваемые ранее процессы в электрических цепях относятся к установившимся. Это такие процессы, при которых напряжение и токи либо неизменны во времени ( цепи постоянного тока ), либо представляют собой периодические функции времени ( цепи переменного тока ).

Наступлению установившегося процесса, отличного от первоначального режима работы, предшествует, как правило, переходный процесс, при котором напряжения и токи изменяются непериодически. Таким образом, переходный процесс возникает в электрической цепи при переходе от одного установившегося состояния к другому. Известно, что определение напряжений и токов в установившемся режиме сводится к нахождению частных решений дифференциальных уравнений электрической цепи. Способы отыскания таких решений были рассмотрены ранее.

Переход от одного режима работы цепи к другому может быть вызван любыми переключениями в этой электрической цепи. Такие переключения называются в электротехнике коммутацией, причем считается, что сам процесс переключения производится мгновенно ( без затрат времени ). Однако, при любом внезапном изменении структуры электрической цепи, имеющиеся запасы энергии электрических и магнитных полей не соответствуют запасам энергии в новом установившемся режиме, после произошедших изменений в электрической цепи.

Но энергия не может измениться скачком ( на конечную величину за бесконечно малый промежуток времени )т.к. это приводит к бесконечно большой мощности ( ).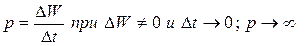

Поэтому новый режим в электрической цепи не устанавливается мгновенно. Время, затрачиваемое на возникновение нового установившегося состояния электрической цепи, называется временем переходного процесса.

Для завершения переходного процесса и наступления установившегося процесса теоретически требуется бесконечно большое время. Практически, время переходного процесса определяется малым интервалом, по истечении которого токи и напряжения настолько приближаются к установившимся, что разница оказывается почти неощутимой. Энергия, накопившаяся в реактивных элементах электрической цепи расходуется ( переходит в тепловую ) на сопротивлениях. Чем интенсивнее этот переход, тем быстрее протекает переходный процесс. Подбирая соответствующие параметры цепи ( элементы R,L,C ) можно ускорить или замедлить переходный процесс.

Переходные процессы могут быть нежелательным и опасными, например, при коротких замыканиях в энергетических системах. Однако, переходные процессы могут представлять собой естественный, нормальный режим работы цепи, например, в радиопередающих или радиоприёмных устройствах или системах автоматического регулирования.

Законы коммутации.

Введем следующие обозначения:

- Будем считать, что отсчет времени коммутации начинается с момента переключения, т.е. t=0.

- Величины токов, напряжений, их производных по времени к моменту, предшествующему коммутации, обозначим (0-), а сразу же после коммутации, обозначим (0₊). Например i_L(0_-) – обозначает ток через индуктивность к моменту коммутации, u_c(0₊)- обозначает напряжение на емкости сразу же после коммутации.

Высказанные ранее положения о невозможности мгновенного изменения энергии электрических или магнитных полей выражают признаки непрерывности во времени потокосцепления индуктивности и электрического заряда емкости. 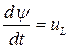. Если потокосцепление изменяется скачком, то , что лишено физического смысла.

Но 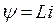, поэтому при L=const ток через индуктивность ( т.е. в цепи с индуктивностью ) не может измениться скачком. Таким образом, ток в цепи с индуктивностью, установившийся к моменту коммутации, равен току в цепи с индуктивностью, появившемуся сразу же после коммутации. Затем, с течением времени, этот ток плавно изменяется. Это можно записать так, используя рассматриваемые выше обозначения: .

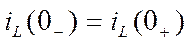Этот закон называется первым законом коммутации.

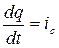если q меняется скачком, то 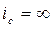, что лишено физического смысла. Так как 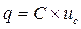, где С – емкость - величина постоянная, то напряжение на емкости не может изменяться скачком. Поэтому, напряжение на емкости, установившееся к моменту коммутации, равно напряжению на емкости, имеющемуся сразу же после коммутации. Затем, с течением времени это напряжение плавно изменяется.

Используя введенные выше обозначения, запишем: 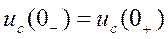. Этот закон называют вторым законом коммутации.

Сказанное ранее отнюдь не означает, что в электрических цепях невозможны скачкообразные изменения токов и напряжений. Например, напряжение на индуктивности и ток через емкость могут изменяться скачком. Возможны скачкообразные изменения токов и напряжений на резисторах.

Начальные условия.

Начальные условия - это значения токов, напряжений и их производных по времени в электрической цепи при t=0. Следует различать докомутационные i(0_-); u(0_-) и послекоммутационные i(0₊); u(0₊) начальные условия. Послекоммутационные начальные условия не всегда равны докоммутационным . Например, .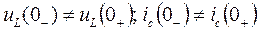

Начальные условия разделяются на независимые и зависимые.

Независимые начальные условия характеризуют энергию магнитного и электрического полей , запасенную к моменту коммутации.

Т.к. 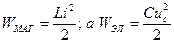, то значения токов через индуктивность и напряжения на емкости к моменту коммутации ( т.е. в докоммутационном режиме ) и есть независимые начальные условия. Следовательно, независимые начальные условия определяются путем расчета токов через индуктивность и напряжений на емкости в докоммутационной схеме (любым методом рассмотренным ранее ). Значения всех остальных величин токов, напряжений и их производных по времени, при t=0₊ ( т.е. после коммутации ) определяемых, например, по законам Кирхгофа,с учётом независимых начальных условий называются зависимыми начальными условиями.

Если при t=0 ( к началу процесса ) токи и напряжения равны нулю, то такие начальные условия называются нулевыми. Например, .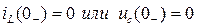

В противном случае начальные условия называются ненулевыми.

4. Принужденный ( установившийся ), свободный и переходный режимы.

Режим работы электрической цепи, задаваемый внешними источниками электрической энергии, называется принужденным или установившимся.

Методы расчетов напряжений и токов в этом режиме изучались ранее.

Режим работы электрической цепи, возникающий при перераспреде-лении энергии магнитного и электрического полей, запасенных в индуктив-ностях и емкостях, включенных в электрическую цепь ( без учета энергии внешних источников ), называется свободным.

Т.к. рассматриваемые электрические цепи линейны, то к ним применим принцип суперпозиции ( наложения ). На основании этого принципа можно переходный режим рассматривать как линейную комбинацию принужденного и свободного режимов, то есть записать следующие соотношения:

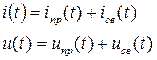
Где i(t) и u(t) – мгновенные значения переходного тока и напряжения.

i_пр(t) и u_пр(t) – принужденные ( установившиеся ) составляющие переходного тока и напряжения.

i_св(t) и u_св(t) – свободные составляющие переходного тока и напряжения.

Процессы, происходящие в электрической цепи описываются дифференциальными уравнениями. Поэтому анализ переходных процессов в линейной электрической цепи с постоянными параметрами R,L,C сводится к решению обыкновенных линейных дифференциальных уравнений, выражающих законы Кирхгофа.

Как известно, общий интеграл такого уравнения равен сумме частного решения неоднородного уравнения и общего решения однородного уравнения.

Частное решение – это режим , задаваемый внешними источниками, т.е. принужденный режим. Общее решение однородного уравнения физически определяет токи и напряжения в электрической цепи при отсутствии внешних источников, т.е. свободные составляющие токов и напряжений.

Таким образом, если цепь состоящая из элементов R,L,C подключается к источнику ЭДС e(t), то дифференциальное уравнение такой цепи ,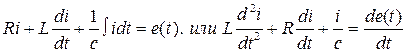

имеет решение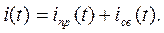

Метод, основанный на непосредственном решении дифференциальных уравнений электрической цепи, связывающих токи и напряжения, называется классическим методом расчета переходный процессов. Постоянные интегрирования определяются исходя из начальных условий и законов коммутации.