Переходный процесс в электрических цепях, описываемых дифференциальными уравнениями первого порядка.
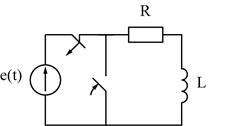
Рассмотрим переходный процесс в электрической цепи, содержащей последовательно соединенные индуктивность и активное сопротивление, подключаемые к источнику ЭДС e(t).
Введем следующие обозначения в электрических схемах.

- В момент t=0 ключ замыкается
- В момент t=0 ключ размыкается
а) Рассмотрим схему включения цепи R,L к источнику ЭДС.
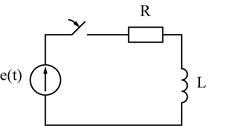
Т.к. последовательно включенные элементы R и L могут быть схемой замещения катушки, то часто эту схему называют “включение катушки к источнику ЭДС.”
Расчёт проводим в следующей последовательности :
1) Определим независимые начальные условия. Т.к. цепь содержит только одну индуктивность, то определим ток через индуктивность в докоммутационной схеме.
i(0-)=0 [А]
2) Начертим послекоммутационую схему и составим дифференциальное уравнение этой цепи.
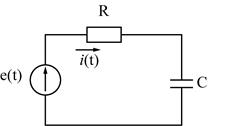
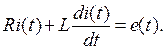
Т.к. токи и напряжения рассматриваются при расчетах переходных процессов, как функции времени, то при дальнейших вычислениях символ “t” опустим, т.е. i(t)=i; u(t)=u; e(t)=e .
3) Записываем решение этого уравнения в виде суммы принужденной и свободной составляющих.
i= iпр+ iсв.
4) Для определения iпр необходимо знать, как задана ЭДС е. Пусть е = Е= const. Тогда 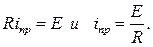
5) Для определения свободной составляющей тока iсв рассмотрим однородное дифференциальное уравнение 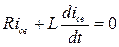 .
.
6) Решим это уравнение.
Характеристическое уравнение
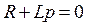 - имеет один корень
- имеет один корень
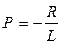
Тогда свободная составляющая пишется в виде: 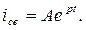
7) Записываем выражение для переходного тока:
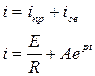
8) Определим постоянную интегрирования А.
При t=0+ имеем:
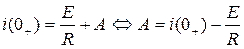
9) На основании первого закона коммутации получаем:
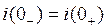 ;
; 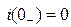
Таким образом i(0+)=0.
10) Вычисляем постоянную интегрирования: 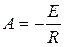
11) Записываем значения переходного тока, как результат решения дифференциального уравнения.
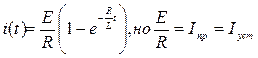
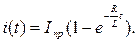
Из курса математического анализа известно, что если функция y=f(t), то подкасательная равна 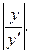 В данном случае при любом значении t величина
В данном случае при любом значении t величина 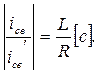
Эта величина обозначается 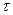 и называется постоянной времени цепи (измеряется в секундах ).
и называется постоянной времени цепи (измеряется в секундах ).
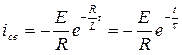 при
при 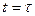 величина свободной составляющей тока убывает в “e”раз. Таким образом, постоянная времени определяется как промежуток времени, по прошествии которого рассматриваемая величина изменяется в “е” раз.
величина свободной составляющей тока убывает в “e”раз. Таким образом, постоянная времени определяется как промежуток времени, по прошествии которого рассматриваемая величина изменяется в “е” раз.
Построим график переходного процесса.
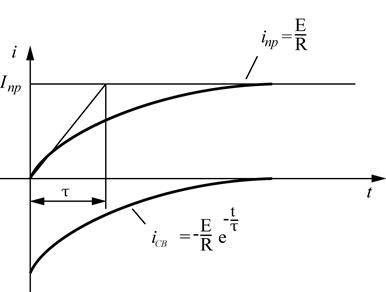
Выражение 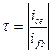 показывает, что постоянная времени графически определяется длинной подкасательной к графику
показывает, что постоянная времени графически определяется длинной подкасательной к графику 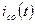 при любом значении t.
при любом значении t.
Можно определить постоянную времени так. При 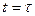
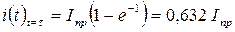 , следовательно, время, за которое ток достигает 63,2% от установившегося значения будет равно постоянной времени.
, следовательно, время, за которое ток достигает 63,2% от установившегося значения будет равно постоянной времени.
Как было отмечено ранее, переходный процесс длится теоретически бесконечно большое время.
Практически время переходного процесса определяется промежутком от 3 до 5 значений постоянной времени, т.е. 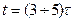 .
.
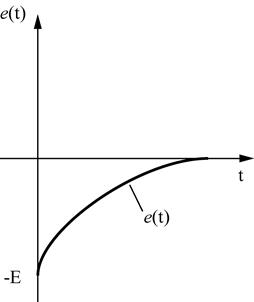
ЭДС самоиндукции 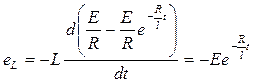
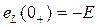 . Т.е. при включении цепи R,L в момент включения возникает ЭДС самоиндукции, полностью компенсирующая ЭДС источника. Поэтому,
. Т.е. при включении цепи R,L в момент включения возникает ЭДС самоиндукции, полностью компенсирующая ЭДС источника. Поэтому, 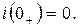 При уменьшении
При уменьшении 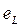 по экспоненциальному закону, по такому же закону изменяется ток
по экспоненциальному закону, по такому же закону изменяется ток 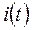 . При
. При 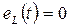 ток достигает установившегося значения, равного
ток достигает установившегося значения, равного 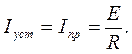 (В полном соответствии с законом Кирхгофа
(В полном соответствии с законом Кирхгофа 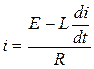 ).
).
Построим зависимость 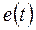 .
.
б) Короткое замыкание цепи R,L.
1). Определим независимые начальные условия. При 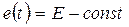 до коммутации
до коммутации 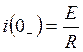
2). Составим схему электрической цепи после коммутации.
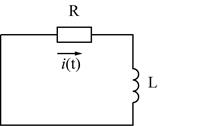
В такой схеме ток существует только за счет энергии магнитного поля индуктивности.
Поэтому, когда вся энергия магнитного поля перейдет в тепловую на сопротивлении R, ток должен прекратиться. Следовательно, 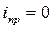 .
.
2). Запишем дифференциальное уравнение этой цепи.
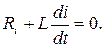
Получим однородное уравнение.
3). Ищем ток в виде суммы принужденной и свободной составляющих 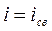 .
.
4). Т.к. уравнение однородное ,то 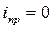 , что совпадает с выводами п.1.
, что совпадает с выводами п.1. 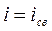 .
.
5). Характеристическое уравнение соответствует уравнению, написанному ранее , т.е. 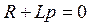 и имеет единственный корень
и имеет единственный корень 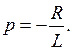
6). Решение для 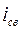 ищем в виде
ищем в виде 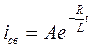 .
.
7). 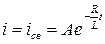 . При t=0 в соответствии с законом коммутации имеем:
. При t=0 в соответствии с законом коммутации имеем: 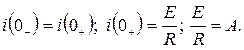
8). Записываем зависимость переходного тока от времени: 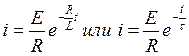 .
.
9). Строим график 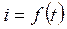
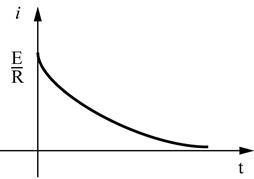
Покажем, что энергия, переходящая в тепло, за время переходного процесса равна энергии магнитного поля индуктивности. Для этого вычислим интеграл: 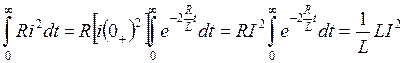 .
.
в) Включение цепи R,L к источнику синусоидальной ЭДС.
Пусть 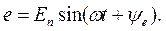
Принужденный ток в этой цепи равен 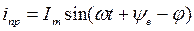 где
где 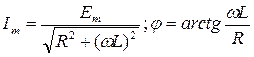 .
.
Тогда 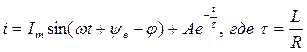
Такая запись возможна ,т.к. свободная составляющая не зависит от внешней ЭДС. И все, сказанное ранее о характеристическом уравнении и свободной составляющей, справедливо и для источника синусоидальной ЭДС.
Т.к. 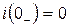 (до включения цепи ток в ней отсутствовал и учитывая, что
(до включения цепи ток в ней отсутствовал и учитывая, что 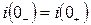 имеем
имеем 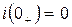 ,
, 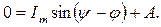
Откуда постоянная интегрирования А равна 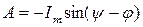 (не зависит от времени).
(не зависит от времени).
Тогда переходный ток равен :
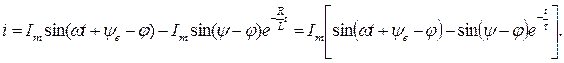
Изобразим график этой зависимости. 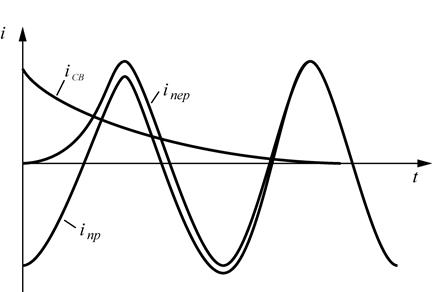
Сделаем некоторые выводы.
1) Начальное значение 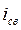 зависит от начальной фазы
зависит от начальной фазы 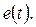 (т.е .угла
(т.е .угла 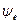 ).
).
2) Наибольшее значение 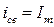 достигается, если
достигается, если 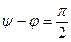 .
.
3) Наибольшее значение переходного тока не превышает 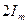 .
.
4) Свободный ток равен нулю ( т.е. в цепи сразу наступает установившийся режим, если 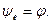
Рассмотрим переходный процесс в цепи, где последовательно включены сопротивления и емкость.
а) Включение такой цепи к источнику ЭДС 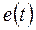 .
.
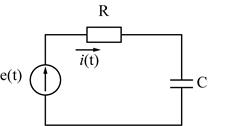
Схема цепи:
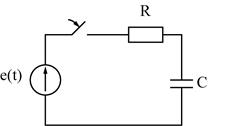
Рассмотрим общий случай, когда конденсатор был заряжен до момента коммутации, т.е. 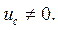
Рассуждения о переходящем процессе будут аналогичны сказанному выше.
1) Определяем независимые начальные условия.
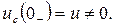
2) Составляем послекоммутационную схему цепи и записываем дифференциальное уравнение для этой цепи.
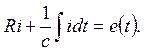
Т.к. будем искать зависимость напряжения на емкости от времени 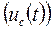 , то перепишем дифференциальное уравнение.
, то перепишем дифференциальное уравнение.
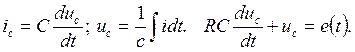
3). Ищем 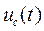 в виде
в виде 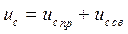 .
.
4). Т.к. 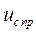 определяется характером ЭДС, то рассмотрим случай, когда
определяется характером ЭДС, то рассмотрим случай, когда 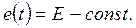 Тогда
Тогда 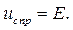
5). Составим характеристическое уравнение 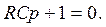
Оно имеет единственный корень 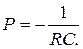
6). Свободную составляющую переходного напряжения ищем в виде 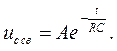
7). Записываем переходное напряжение 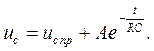
8). Рассматриваем значения напряжения 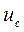 при
при 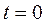 имеем:
имеем:
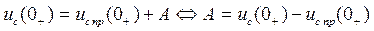 .
.
9). Т.к. при 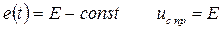 (п.4), а по закону коммутации
(п.4), а по закону коммутации
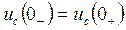 , то
, то 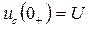 .
.
10). Тогда 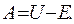
11). Окончательно получаем:
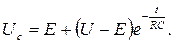
Т.к. при 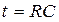 свободная составляющая напряжение уменьшается в «е» раз,
свободная составляющая напряжение уменьшается в «е» раз, 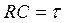 - постоянная времени.
- постоянная времени.
При нулевых начальных условиях 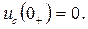 и
и 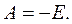
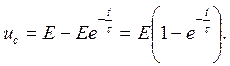
Определим теперь переходный ток в цепи с емкостью.
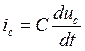
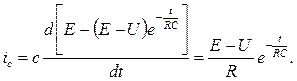
Построим графики переходного напряжения и тока в цепи RC.
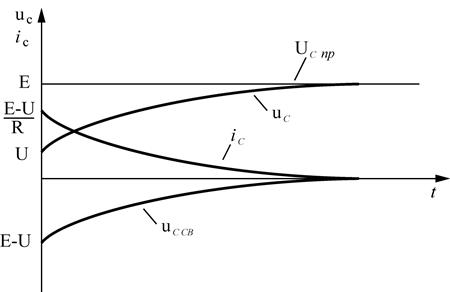
При нулевых начальных условиях
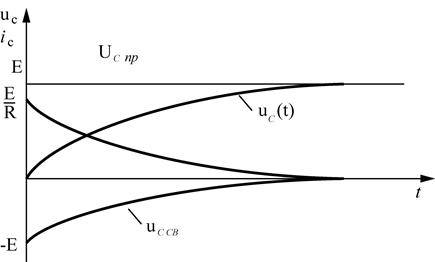
б) Короткое замыкание в цепи RC. ( разряд емкости на сопротивление ).
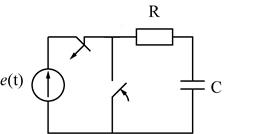
1) Определяем независимые начальные условия. 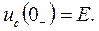
2) Записываем дифференциальное уравнение для послекоммутационной схемы. 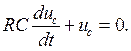
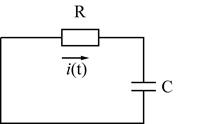
3). Т.к. уравнение однородное , то 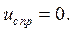 ( По окончании переходного процесса конденсатор полностью разряжается ).
( По окончании переходного процесса конденсатор полностью разряжается ).
4). Тогда 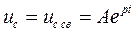 .
.
5). Характеристическое уравнение 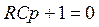 имеет единственный корень
имеет единственный корень 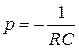 .
.
6) Определяем постоянную интегрирования.
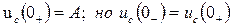 следовательно
следовательно 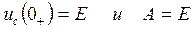 .
.
7) Записываем уравнения переходного напряжения 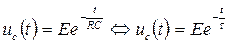 .
.
8) Записываем уравнения переходного тока.

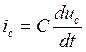
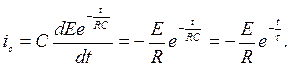
9) Строим графики переходного напряжения 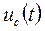 и переходного тока
и переходного тока 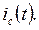
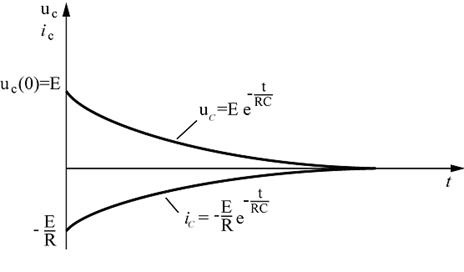
Покажем, что энергия рассеиваемая на сопротивлении R в течение всего переходного процесса равна энергии электрического поля емкости.
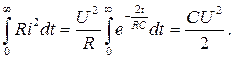
в) Включение цепи RC к источнику синусоидального напряжения.
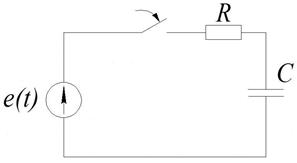
Пусть 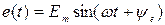 .
.
Принужденный (установившийся) ток в такой цепи равен:
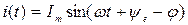 , где
, где
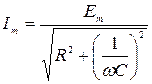 ;
; 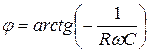 .
.
Ищем переходное напряжение на емкости UC(t) в виде суммы принужденной и свободной составляющих, т.е.
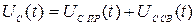 .
.
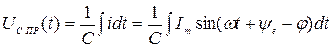 .
.
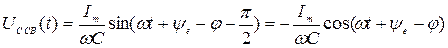 .
.
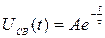 , где
, где 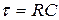 .
.
Если начальное напряжение на емкости равно нулю (нулевые начальные условия), то в соответствии с 2-м законом коммутации
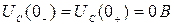 .
.
Тогда имеем:
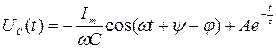 и
и
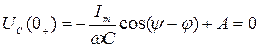 .
.
Окончательно получаем закон изменения напряжения на емкости в виде:
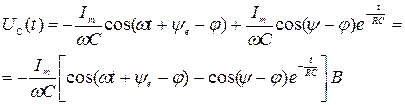
Определим переходной ток:
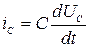 .
.
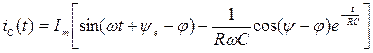 .
.
Сделаем некоторые выводы:
1. Начальное значение UCB зависит от начальной фазы ЭДС.
2. Если 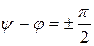 , то свободной составляющей напряжения на емкость не возникает и в цепи сразу без переходного процесса наступает принужденный установившийся режим.
, то свободной составляющей напряжения на емкость не возникает и в цепи сразу без переходного процесса наступает принужденный установившийся режим.
3. Если 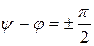 , то значение принужденного тока достигает максимума.
, то значение принужденного тока достигает максимума.
4. Если 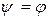 , то начальное значение переходного напряжения будет наибольшим.
, то начальное значение переходного напряжения будет наибольшим.
Дата добавления: 2017-01-26; просмотров: 4768;











