Методы первого порядка

Градиентный метод. Будем рассматривать задачу (3.5.2), предполагая, что функция 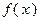непрерывно дифференцируема на 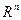. Выражение для дифференциала функции

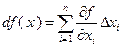
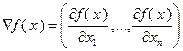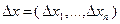является скалярным произведением векторов и , т.е. .

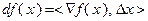Вектор 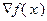называют градиентом функции 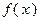и обозначают иногда grad 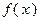( 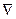читается «набла»).

Понятие градиента удобно использовать для краткой записи производной по направлению 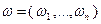, где 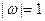. Имеем

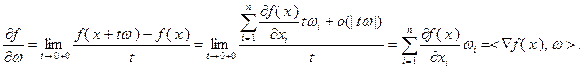
Производная по направлению обладает следующим свойством: 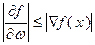. Для доказательства воспользуемся неравенством Коши – Буняковского для скалярного произведения векторов:

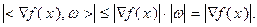
При этом 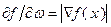, если 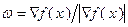. Таким образом, модуль производной по направлению 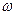не превосходит модуля градиента функции, причем наибольшее (неотрицательное) значение производной по направлению 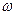имеет место в случае, если вектор 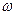направлен по градиенту функции 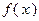(быстрее всего функция 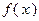возрастает по направлению градиента функции). Отсюда следует, что направлением нибыстрейшего убывания функции 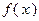является направление ее антиградиента .

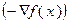Это свойство градиента лежит в основе ряда итерационных методов минимизации функций, одним из которых является градиентный метод. Как и другие итерационные методы, градиентный метод предполагает выбор начального приближения – некоторой точки 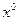. Общих правил выбора точки 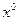нет, однако при наличии соответствующих априорных данных начальное приближение стараются выбрать поближе к области расположения точки (или точек) минимума целевой функции задачи.

Будем считать, что некоторая начальная точка 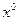уже выбрана. Градиентный метод заключается в построении последовательности 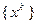в соответствии с выражением

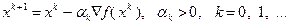(3.5.23)

Здесь 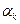– шаговый множитель. Если 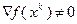, то шаг 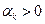можно выбрать так, чтобы было выполнено условие 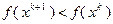. Действительно,

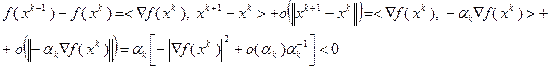
при всех достаточно малых 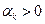. Если 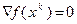, то 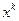– стационарная точка. В этом случае процесс (3.5.23) прекращается, и при необходимости проводится дополнительное исследование поведения функции в окрестности точки 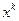с целью выяснения, является ли эта точка точкой минимума функции 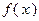. Если 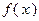– выпуклая функция на 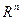, то в стационарной точке всегда достигается минимум.

В зависимости от способа выбора величины 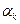в (3.5.23) можно получить различные варианты градиентного метода. Рассмотрим некоторые наиболее употребительные из них.

1). На луче 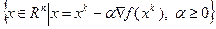, направленном по антиградиенту, введем функцию одной переменной

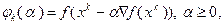(3.5.24)

и определим 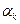в виде

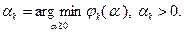(3.5.25)

Метод (3.5.23) – (3.5.25) называют методом скорейшего спуска. При 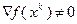получаем 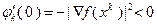, поэтому минимум функции 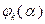может достигаться лишь при 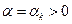, что и отражено в (3.5.25). Следующий пример иллюстрирует случай, когда величина 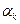, определяемая согласно (3.5.25), может быть получена в явном виде.

Пусть дана квадратичная функция

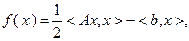(3.5.26)

где 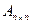– симметрическая положительно определенная матрица, 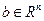. Функция (3.5.26) сильно выпукла на 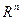, при этом 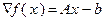и метод (3.5.23) в данном случае записывается в виде:

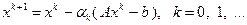
Таким образом, градиентный метод для функции (3.5.26) представляет собой известный итерационный метод решения системы линейных алгебраических уравнений 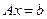. Используя выражение для приращения рассматриваемой функции

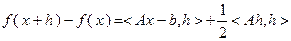и формулу (3.5.24), в которой величине 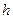соответствует 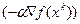, получим

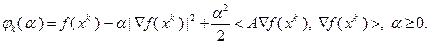
При 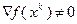из условия 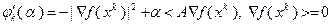находим

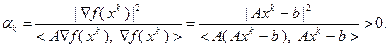
Поскольку функция 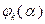выпукла, в найденной точке 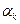она достигает своего минимума при .

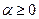Однако в общем случае точное определение величины 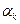из условий (3.5.25) не всегда возможно. В связи с этим на практике часто ограничиваются нахождением величины 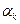, приближенно удовлетворяющей условиям (3.5.25). При этом выбор 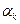возможен, например, из условий

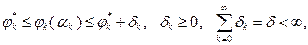(3.5.27)

или из условий

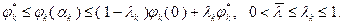(3.5.28)

В выражениях (3.5.27), (3.5.28) 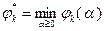, а величины 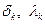характеризуют погрешность выполнения условий (3.5.25): чем ближе 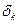к нулю или 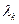к единице, тем меньше расхождение между 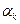, найденным из условий (3.5.27), (3.5.28) и значением 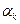, определяемым условиями (3.5.25).

Следует отметить, что антиградиент 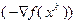указывает направление быстрейшего спуска лишь в достаточно малой окрестности точки 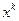. Это означает, что если функция 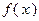меняется быстро, то в следующей точке 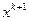направление антиградиента 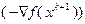может сильно отличаться от направления 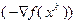. Поэтому слишком точное определение величины 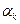из условий (3.5.25) не всегда целесообразно.

2). На практике нередко ограничиваются нахождением какого-либо 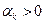, обеспечивающего выполнение условия монотонности: 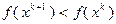. С этой целью задается некоторое значение 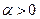, которое используется в выражении (3.5.23) в качестве постоянного шагового множителя до тех пор, пока сохраняется монотонность. При нарушении условия монотонности 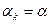дробят до тех пор, пока условие монотонности не будет выполнено. В алгоритмах, реализующих данный подход, предусматривается также возможность увеличения значения 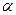с сохранением условия монотонности.

3). Если функция 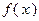непрерывно дифференцируема на 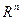и градиент 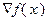удовлетворяет условию Липшица

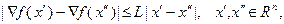(3.5.29)

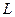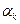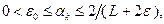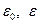причем константа известна, то в (3.5.23) в качестве может быть взято любое число, удовлетворяющее условиям где – положительные числа, являющиеся параметрами метода. В частности, при 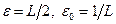получим метод (3.5.23) с постоянным шагом .

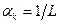4). Возможен выбор 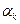из условия

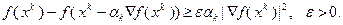(3.5.30)

Для выполнения условия (3.5.30) сначала обычно устанавливают шаговый множитель постоянным для всех итераций: 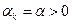(например, 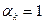), а затем при необходимости дробят его, изменяя по закону 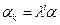( 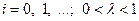) до тех пор, пока впервые не выполнится условие (3.5.30).

5). Возможно априорное задание величин 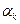, исходя из условий

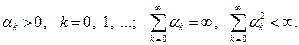
Например, в качестве 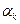можно взять 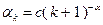, где 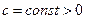, а число 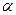удовлетворяет неравенству 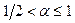. Тогда при 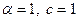получим 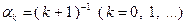. Такой выбор 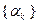в (3.5.23) прост для реализации, но не гарантирует выполнения условия монотонности 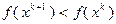и в общем случае не обеспечивает быстрой сходимости.

6). В тех случаях, когда заранее известна величина 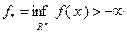, в (3.5.23) можно принять 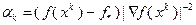– это абсцисса точки пересечения прямой 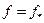с касательной к кривой 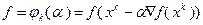в точке .

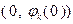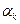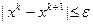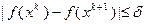Вне зависимости от способа определения на практике итерации (3.5.23) продолжают до тех пор, пока не будет выполнен некоторый критерий окончания счета. В качестве такого критерия часто используют: , или , или 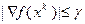, где 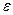, , 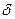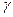– заданные числа. Иногда заранее задают число итераций; возможны также сочетания этих и других критериев. Приведенные критерии не гарантируют окончания счета вблизи от искомой точки минимума. Надежных критериев окончания счета, гарантирующих получение решения задачи нелинейного программирования с требуемой точностью и применимых к широкому классу задач, пока нет.

Пусть градиент функции 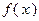удовлетворяет условию Липшица с постоянной 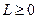, т.е.

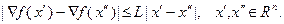(3.5.31)

Тогда градиентный метод (3.5.23) с постоянным шаговым множителем 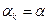, удовлетворяющим условию 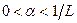, сходится к стационарным точкам функции .

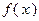Для доказательства этого утверждения рассмотрим точки 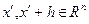с условием, что 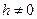, 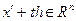при всех 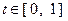. Тогда можно рассматривать функцию одной переменно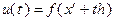й при 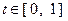. Для приращения функции 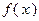, дифференцируемой в точке 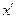, можно записать:

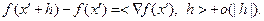(3.5.32)

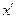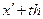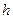Заменив в выражении (3.5.32) на , на 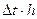, получим

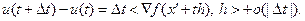(3.5.33)

Разложение (3.5.33) указывает на справедливость формулы:

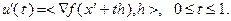(3.5.34)

Для функции одной переменной можно записать:

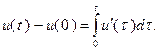
Полагая в последнем выражении 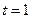и используя (3.5.34), получим:

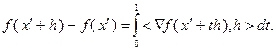(3.5.35)

Использование выражения (3.5.35) позволяет записать:

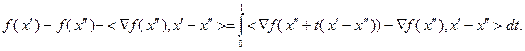
Отсюда, с учетом (3.5.31) и неравенства Коши – Буняковского, следует:

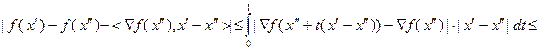
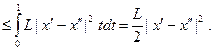(3.5.36)

Соотношение (3.5.36) позволяет записать:

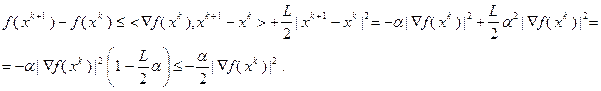
Здесь использована формула (3.5.23) с учетом 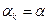, а также условие 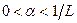. Используя полученный результат, запишем:

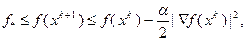(3.5.37)

где 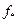– значение функции 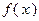в стационарной точке. Из (3.5.37) следует, что последовательность 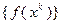монотонна и ограничена. Следовательно, она является сходящейся, что позволяет записать:

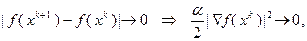
и, таким образом, 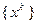сходится к множеству стационарных точек, т.е. точек, в которых градиент функции 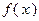равен нулю. Для задач выпуклого программирования полученный результат означает сходимость к оптимальной точке, т.е. к решению задачи.

Метод скорейшего спуска имеет следующий геометрический смысл: точка 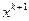, определяемая соотношениями (3.5.23), (3.5.25), лежит на луче 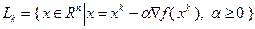в точке его касания линии уровня (при 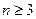– поверхности уровня) 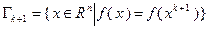, а сам луч 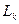перпендикулярен к линии уровня 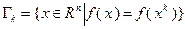– см. рис. 3.5.1. Действительно, пусть 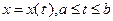– некоторое параметрическое уравнение линии уровня 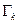, т.е.

Рис. 3.5.1. Геометрическая интерпретация метода скорейшего спуска

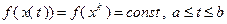, причем 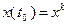. Тогда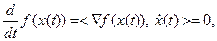 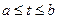. В частности, при 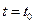имеем 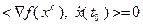. Это означает, что градиент (или антиградиент) 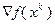перпендикулярен к касательному направлению поверхности уровня 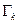в точке 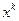или, иначе говоря, луч 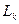перпендикулярен к 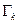. Из (3.5.24) с учетом (3.5.25) при 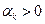получаем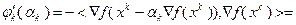 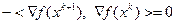. Но вектор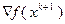

перпендикулярен к 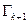в точке 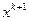, поэтому последнее равенство означает, что направление 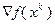и, следовательно, луч 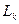являются касательными к линии уровня 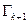в точке .

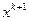Чем ближе линии уровня 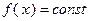к окружности, тем лучше сходится метод скорейшего спуска. Теоретические исследования и численные эксперименты подтверждают, что метод скорейшего спуска и другие варианты градиентного метода медленно сходятся в тех случаях, когда поверхности уровня функции 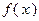сильно вытянуты и функция имеет так называемый «овражный» характер. Это означает, что небольшое изменение некоторых переменных приводит к резкому изменению значений функции – эта группа переменных характеризует «склон оврага», а по остальным переменным, задающим направление «дна оврага», функция меняется незначительно. Если точка находится на «склоне оврага», то направление спуска из этой точки будет почти перпендикулярным к направлению «дна оврага», и в результате приближения 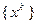, получаемые градиентным методом, будут поочередно находиться то на одном, то на другом «склоне оврага». Если «склоны оврага» достаточно круты, то такие скачки со «склона на склон» точек 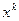могут сильно замедлить сходимость градиентного метода.

Для ускорения сходимости при поиске минимума «овражной» функции разработаны «овражные» модификации градиентного метода, смысл которых состоит в отыскании и уточнении направления «оврага» и дальнейшем продвижении в этом направлении. Одна из таких модификаций заключается в следующем. В начале поиска задаются две точки 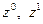, из которых производят спуск с помощью какого-либо варианта градиентного метода, и получают две точки 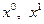на «дне оврага». 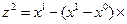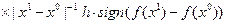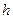Затем полагают , где – положительная постоянная, называемая «овражным» шагом. Из точки 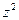, которая находится на «склоне оврага», производят спуск с помощью градиентного метода и определяют следующую точку 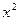на «дне оврага». Если уже известны точки 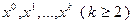, то из точки 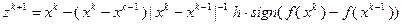совершают спуск с помощью градиентного метода и находят следующую точку 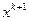на «дне оврага».

Величина овражного шага 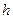подбирается эмпирически с учетом информации о минимизируемой функции, получаемой в ходе поиска минимума. От правильного выбора 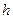существенно зависит скорость сходимости метода.

Метод проекции градиента. Пусть рассматривается задача

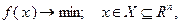(3.5.38)

где множество 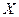необязательно совпадает со всем пространством 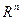, а функция 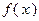непрерывно дифференцируема на 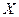. Непосредственное применение рассмотренного выше градиентного метода в случае 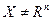может привести к затруднениям, так как точка 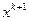из (3.5.23) при каком-то 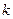может не принадлежать 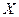. Однако эту трудность можно преодолеть, если полученную с помощью формулы (3.5.23) точку 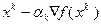при каждом 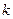проецировать на множество .

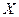Напомним, что проекцией точки 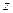из 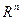называется ближайшая к 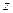точка 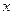множества 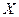, т.е. точка 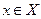, удовлетворяющая условию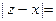 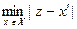. Проекцию точки 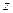на множество 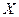будем обозначать через .

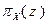Пусть 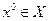– некоторое начальное приближение. Далее последовательность 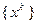строится по правилу

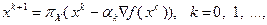(3.5.39)

где 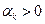. Если 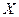– выпуклое замкнутое множество и способ выбора 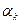в (3.5.39) задан, то последовательность 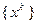однозначно определяется выражением (3.5.39). В частности, при 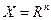метод (3.5.39) превращается в градиентный метод.

Если в (3.5.39) на некоторой итерации оказалось 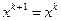(например, это произойдет при 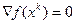), то процесс прекращают. В этом случае точка 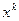удовлетворяет необходимому условию оптимальности, и для выяснения того, является ли в действительности 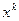решением задачи (3.5.38) или нет, при необходимости нужно провести дополнительное исследование функции 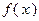в окрестности точки 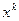. В частности, если 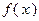– выпуклая функция, то такая точка 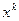является решением задачи (3.5.38).

Метод линеаризации. В этот методе на каждой итерации используются линейные аппроксимации целевой функции и функций, задающих ограничения. Рассмотрим его применительно к решению задачи

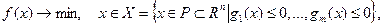(3.5.40)

где 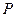– выпуклое замкнутое множество и функции 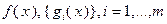, непрерывно дифференцируемы на 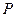. Пусть 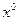– начальное приближение, 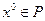. Предположим, что 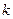-е приближение 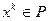при некотором 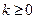уже известно. Введем функцию

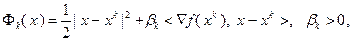(3.5.41)

и множество

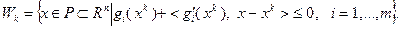(3.5.42)

Пусть 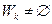. В качестве 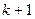-го приближения 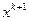возьмем решение следующей задачи минимизации:

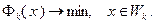(3.5.43)

Поскольку функция (3.5.41) сильно выпукла, множество (3.5.42) выпукло и замкнуто, задача (3.5.43) имеет решение, притом единственное. Задачу (3.5.43) необязательно решать точно: достаточно найти точку 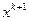из условий

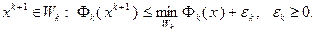(3.5.44)

Рассмотренный вариант метода линеаризации обычно используют в тех случаях, когда определение точки 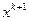из (3.5.44) не требует слишком большого объема вычислений. Отметим также, что задача (3.5.43) равносильна задаче

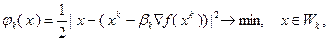
так как 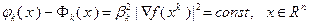. Это значит, что точное решение 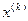задачи (3.5.43) представляет собой проекцию точки 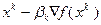на множество 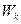, а точка 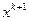из (3.5.44) является приближением для 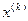. Отсюда следует, что если в (3.5.40) ограничения 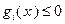отсутствуют ( 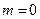), то 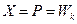и метод линеаризации превратится в метод проекции градиента.