ИССЛЕДОВАНИЕ ЗАДАЧИ МАТЕМАТИЧЕСКОГО
ПРОГРАММИРОВАНИЯ
Постановка общей задачи математического программирования может быть представлена в виде:
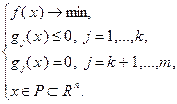 (3.4.1)
(3.4.1)
Здесь в качестве 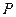 рассматривается множество простой структуры (шар, параллелепипед, пространство
рассматривается множество простой структуры (шар, параллелепипед, пространство 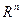 , неотрицательный ортант
, неотрицательный ортант 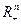 ). Следует отметить, что к задачам типа (3.4.1) относятся задачи линейного программирования. Важным классом задач математического программирования являются задачи выпуклого программирования, т.е. задачи минимизации (или максимизации) выпуклых функций на выпуклых множествах. В этом случае в (3.4.1)
). Следует отметить, что к задачам типа (3.4.1) относятся задачи линейного программирования. Важным классом задач математического программирования являются задачи выпуклого программирования, т.е. задачи минимизации (или максимизации) выпуклых функций на выпуклых множествах. В этом случае в (3.4.1) 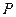 – заданное выпуклое множество; функции
– заданное выпуклое множество; функции 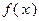 ,
, 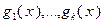 выпуклы на
выпуклы на 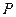 ,
, 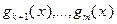 – линейные функции, т.е.
– линейные функции, т.е. 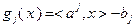 при
при 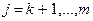 ;
; 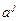 – заданные векторы из
– заданные векторы из 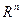 ,
, 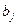 – заданные числа. При этом не исключаются возможности, когда отсутствуют либо ограничения типа неравенств
– заданные числа. При этом не исключаются возможности, когда отсутствуют либо ограничения типа неравенств 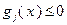 (
( 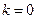 ), либо ограничения типа равенств
), либо ограничения типа равенств 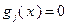 (
( 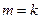 ), либо оба эти вида ограничений. Во всех отмеченных случаях допустимое множество задачи является выпуклым. Среди задач математического программирования выделяют также класс задач, формулируемых в виде так называемой классической задачи. Классической задачей математического программирования является задача, сформулированная в виде:
), либо оба эти вида ограничений. Во всех отмеченных случаях допустимое множество задачи является выпуклым. Среди задач математического программирования выделяют также класс задач, формулируемых в виде так называемой классической задачи. Классической задачей математического программирования является задача, сформулированная в виде:
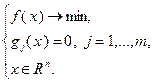 (3.4.2)
(3.4.2)
Другой важной разновидностью задач математического программирования являются задачи квадратичного программирования. Задача квадратичного программирования формулируется в виде:
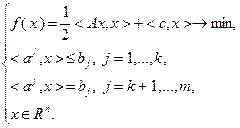 (3.4.3)
(3.4.3)
Здесь 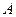 – симметрическая неотрицательно определенная матрица (т.е.
– симметрическая неотрицательно определенная матрица (т.е. 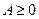 ) размерности
) размерности 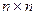 ;
; 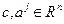 ,
, 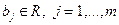 . При этом допускаются случаи
. При этом допускаются случаи 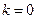 , или
, или 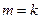 , или
, или 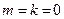 . В задаче (3.4.3) квадратичная выпуклая функция минимизируется на многогранном множестве (многогранное множество иначе называют полиэдром). Такие задачи возникают в различных приложениях. Примерами задач квадратичного программирования являются задачи определения расстояния от точки до многогранного множества, проектирования на такое множество, когда матрица
. В задаче (3.4.3) квадратичная выпуклая функция минимизируется на многогранном множестве (многогранное множество иначе называют полиэдром). Такие задачи возникают в различных приложениях. Примерами задач квадратичного программирования являются задачи определения расстояния от точки до многогранного множества, проектирования на такое множество, когда матрица 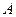 в (3.4.3) является единичной. Задачи квадратичного программирования возникают также как вспомогательные при описании различных методов минимизации. Существующие методы позволяют получать решение задачи (3.4.3) за конечное число шагов (примером такого метода является метод сопряженных градиентов).
в (3.4.3) является единичной. Задачи квадратичного программирования возникают также как вспомогательные при описании различных методов минимизации. Существующие методы позволяют получать решение задачи (3.4.3) за конечное число шагов (примером такого метода является метод сопряженных градиентов).
Рассмотрим подход к исследованию задачи (3.4.2), основанный на использовании метода множителей Лагранжа. Этот метод заключается в следующем. Вводится функция Лагранжа
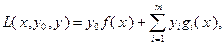 (3.4.4)
(3.4.4)
где 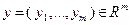 ,
, 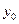 – скалярная переменная,
– скалярная переменная, 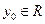 . Последующее использование этой функции вытекает из результатов теоремы 3.4.1.
. Последующее использование этой функции вытекает из результатов теоремы 3.4.1.
Теорема 3.4.1
Пусть функции 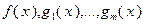 непрерывно дифференцируемы в окрестности точки
непрерывно дифференцируемы в окрестности точки 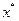 ,
, 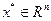 . Тогда если
. Тогда если 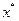 – локальное решение задачи (3.4.2), то необходимо существуют числа
– локальное решение задачи (3.4.2), то необходимо существуют числа 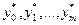 (называемые множителями Лагранжа), не все равные нулю, такие, что
(называемые множителями Лагранжа), не все равные нулю, такие, что
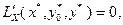 (3.4.5)
(3.4.5)
где 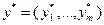 .
.
Доказательство. С учетом (3.4.4) выражение (3.4.5) может быть записано в виде:
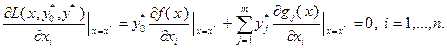 (3.4.6)
(3.4.6)
Поскольку не все числа 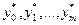 равны нулю, из (3.4.6) следует, что векторы
равны нулю, из (3.4.6) следует, что векторы 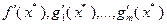 линейно зависимы. Допустим противное: пусть эти векторы линейно независимы. Тогда
линейно зависимы. Допустим противное: пусть эти векторы линейно независимы. Тогда 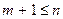 . В случае
. В случае 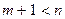 возьмем какие-либо векторы
возьмем какие-либо векторы 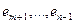 так, чтобы система
так, чтобы система 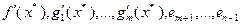 образовала базис в
образовала базис в 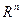 .
.
Введем функции 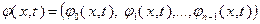 переменных
переменных 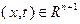 , где
, где 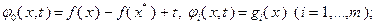
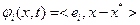
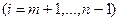 . Рассмотрим систему уравнений:
. Рассмотрим систему уравнений:
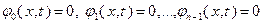
относительно 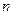 неизвестных
неизвестных 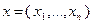 . Для ее исследования воспользуемся теоремой о неявных функциях. Заметим, что
. Для ее исследования воспользуемся теоремой о неявных функциях. Заметим, что 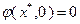 .
.
Далее, функции 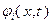 непрерывно дифференцируемы в окрестности точки
непрерывно дифференцируемы в окрестности точки 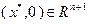 , причем
, причем 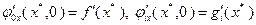
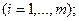
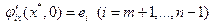 . Это значит, что в точке
. Это значит, что в точке 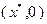 якобиан системы функций
якобиан системы функций 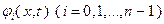 , представляющий собой определитель квадратной матрицы со строками
, представляющий собой определитель квадратной матрицы со строками 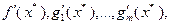
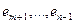 , образующими базис в
, образующими базис в 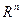 , отличен от нуля. Тогда по теореме о неявных функциях система
, отличен от нуля. Тогда по теореме о неявных функциях система 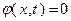 имеет решение при каждом
имеет решение при каждом 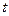
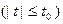 , где
, где 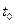 – достаточно малое положительное число, или, точнее, существует вектор-функция
– достаточно малое положительное число, или, точнее, существует вектор-функция 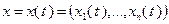 , которая определена и дифференцируема при всех
, которая определена и дифференцируема при всех 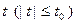 и такая, что
и такая, что
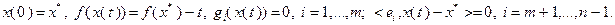
Это значит, что 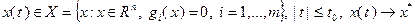 при
при 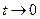 .
.
Отсюда также следует:
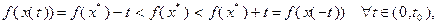
что противоречит тому, что 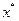 – локальное решение задачи (3.4.2). Таким образом, точка
– локальное решение задачи (3.4.2). Таким образом, точка 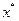 может быть точкой локального минимума лишь в том случае, если выполнение условия (3.4.5) имеет место, когда не все числа
может быть точкой локального минимума лишь в том случае, если выполнение условия (3.4.5) имеет место, когда не все числа 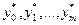 равны нулю. Теорема доказана.
равны нулю. Теорема доказана.
Из доказанной теоремы следует, что подозрительными на экстремум могут быть лишь те точки 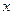 , для которых существуют множители
, для которых существуют множители 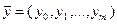 такие, что точка
такие, что точка 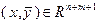 удовлетворяет системе
удовлетворяет системе 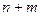 уравнений
уравнений
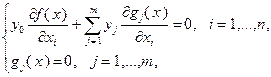 (3.4.7)
(3.4.7)
и, кроме того, известно, что 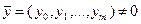 . Справедливо также утверждение, состоящее в том, что всякое решение задачи (3.4.2) удовлетворяет системе (3.4.7). Поэтому для отыскания решения задачи (3.4.2) следует найти все решения системы (3.4.7), для каждого из них вычислить значение целевой функции
. Справедливо также утверждение, состоящее в том, что всякое решение задачи (3.4.2) удовлетворяет системе (3.4.7). Поэтому для отыскания решения задачи (3.4.2) следует найти все решения системы (3.4.7), для каждого из них вычислить значение целевой функции 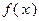 и затем, сравнив полученные значения целевой функции, определить точку, являющуюся искомым решением.
и затем, сравнив полученные значения целевой функции, определить точку, являющуюся искомым решением.
Нетрудно заметить, что если 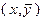 – решение системы (3.4.7), то
– решение системы (3.4.7), то 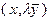 при любом
при любом 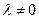 также является решением этой системы. Поэтому множители
также является решением этой системы. Поэтому множители 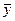 можно подчинить какому-либо дополнительному условию нормировки, например,
можно подчинить какому-либо дополнительному условию нормировки, например,
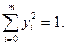 (3.4.8)
(3.4.8)
Добавив уравнение (3.4.8) к уравнениям (3.4.7), получим систему из 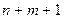 уравнений.
уравнений.
Если система (3.4.7) имеет решения 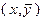 такие, что
такие, что 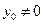 , то задачу (3.4.2) называют регулярной (невырожденной) в точке
, то задачу (3.4.2) называют регулярной (невырожденной) в точке 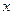 . В регулярной задаче в качестве условия нормировки можно использовать условие
. В регулярной задаче в качестве условия нормировки можно использовать условие 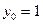 . Нетрудно видеть, что для регулярности задачи в точке
. Нетрудно видеть, что для регулярности задачи в точке 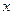 достаточно, чтобы векторы
достаточно, чтобы векторы 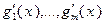 были линейно независимы, т.е. чтобы равенство
были линейно независимы, т.е. чтобы равенство 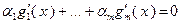 было возможно только при
было возможно только при 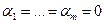 .
.
Метод множителей Лагранжа может быть применен для поиска экстремумов функции и в тех случаях, когда на переменные наряду с ограничениями типа равенств накладываются еще и ограничения типа неравенств:
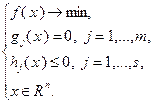 (3.4.9)
(3.4.9)
Предположим, что функции 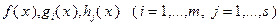 не только определены, но и дифференцируемы во всех точках
не только определены, но и дифференцируемы во всех точках 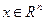 . Оказывается, если ввести новые вспомогательные переменные
. Оказывается, если ввести новые вспомогательные переменные 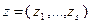 , связанные с исходными переменными соотношениями
, связанные с исходными переменными соотношениями
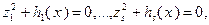 (3.4.10)
(3.4.10)
то задача поиска экстремумов функции 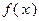 при ограничениях задачи (3.4.9) сводится к равносильной задаче поиска экстремумов той же функции в пространстве переменных
при ограничениях задачи (3.4.9) сводится к равносильной задаче поиска экстремумов той же функции в пространстве переменных 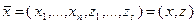 при ограничениях типа равенств
при ограничениях типа равенств 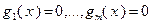 и (3.4.10). Равносильность этих двух задач понимается в следующем смысле: если
и (3.4.10). Равносильность этих двух задач понимается в следующем смысле: если 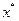 – локальное решение задачи (3.4.9), то
– локальное решение задачи (3.4.9), то 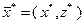 , где
, где 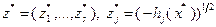
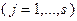 будет локальным решением задачи
будет локальным решением задачи
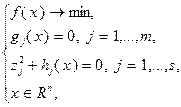 (3.4.11)
(3.4.11)
и наоборот, если 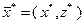 – локальное решение задачи (3.4.11), то
– локальное решение задачи (3.4.11), то 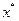 является локальным решением задачи (3.4.9).
является локальным решением задачи (3.4.9).
Таким образом, для решения задачи (3.4.11) можно использовать функцию Лагранжа
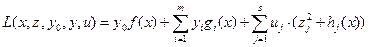 (3.4.12)
(3.4.12)
и в соответствии с вышеизложенным записать необходимые условия экстремума в виде системы (3.4.7), найти точки, подозрительные на экстремум, выявить среди них решение задачи (3.4.11) и затем, исключив из него значения 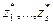 , получить искомое решение задачи (3.4.9) в виде
, получить искомое решение задачи (3.4.9) в виде 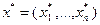 .
.
Пример 3.4.1
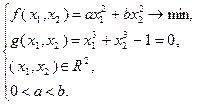
Заданная функция 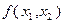 является сильно выпуклой на
является сильно выпуклой на 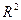 , т.к.
, т.к. 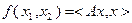 , где
, где 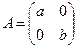 ,
, 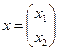 и
и 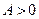 . Следовательно, задача имеет решение. Найдем это решение с помощью необходимого условия существования экстремума. Функция Лагранжа (3.4.4) в данном случае имеет вид:
. Следовательно, задача имеет решение. Найдем это решение с помощью необходимого условия существования экстремума. Функция Лагранжа (3.4.4) в данном случае имеет вид:
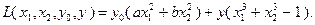
Вычислим частные производные функции Лагранжа по переменным 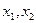 :
:
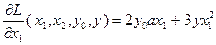 ,
, 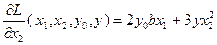
и составим систему уравнений вида (3.4.7):
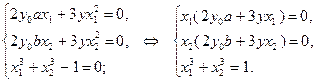 (3.4.13)
(3.4.13)
Анализируя полученную систему, приходим к выводу о том, что случай 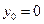 невозможен. Это объясняется тем, что при
невозможен. Это объясняется тем, что при 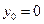 , согласно теореме 3.4.1,
, согласно теореме 3.4.1, 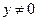 и из первых двух уравнений системы следует
и из первых двух уравнений системы следует 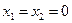 , однако эта пара значений не удовлетворяет третьему уравнению. Поэтому положим
, однако эта пара значений не удовлетворяет третьему уравнению. Поэтому положим 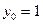 . Здесь мы подразумеваем использование нормирующего множителя
. Здесь мы подразумеваем использование нормирующего множителя 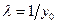 ,
, 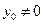 , так как если
, так как если 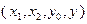 – решение системы (3.4.13), то
– решение системы (3.4.13), то 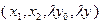 , где
, где 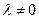 , также будет являться ее решением. Подставим в систему (3.4.13) значение
, также будет являться ее решением. Подставим в систему (3.4.13) значение 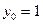 и найдем ее решения:
и найдем ее решения:
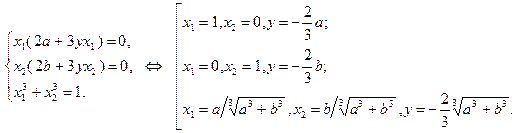
На каждом из найденных решений вычислим значения целевой функции 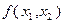 и определим минимальное из них:
и определим минимальное из них:
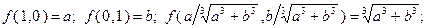
поскольку 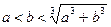 , значение
, значение 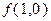 является минимальным. Таким образом,
является минимальным. Таким образом, 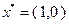 есть искомое решение задачи.
есть искомое решение задачи.
Выше метод множителей Лагранжа был рассмотрен применительно к исследованию задач (3.4.2) и (3.4.9). С помощью функции Лагранжа было сформулировано необходимое условие оптимальности. Важная роль принадлежит функции Лагранжа и при исследовании более общей задачи (3.4.1). Соответствующая теорема, доказательство которой можно найти, например, в [1], формулируется следующим образом.
Теорема 3.4.2
Пусть точка 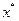 – локальное решение задачи (3.4.1), функции
– локальное решение задачи (3.4.1), функции 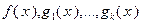 дифференцируемы в точке
дифференцируемы в точке 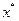 , функции
, функции 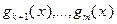 непрерывно дифференцируемы в некоторой окрестности точки
непрерывно дифференцируемы в некоторой окрестности точки 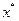 ,
, 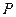 – выпуклое множество. Тогда существуют не все равные нулю числа
– выпуклое множество. Тогда существуют не все равные нулю числа 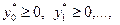
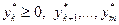 такие, что
такие, что 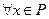 выполнены соотношения:
выполнены соотношения:
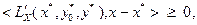 (3.4.14)
(3.4.14)
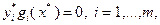 (3.4.15)
(3.4.15)
где 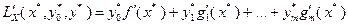 – градиент функции
– градиент функции 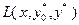 переменной
переменной 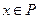 в точке
в точке 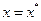 .
.
Ограничение 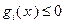 , где
, где 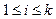 , называют активным (пассивным) в точке
, называют активным (пассивным) в точке 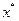 , если
, если 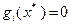 (
( 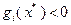 ). Из условий (3.4.15), часто называемых условиями дополняющей нежесткости, следует, что множители Лагранжа
). Из условий (3.4.15), часто называемых условиями дополняющей нежесткости, следует, что множители Лагранжа 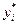 , соответствующие пассивным ограничениям типа неравенств, равны нулю.
, соответствующие пассивным ограничениям типа неравенств, равны нулю.
Задачу (3.4.1) называют регулярной (невырожденной) в точке 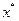 , если существуют множители Лагранжа
, если существуют множители Лагранжа 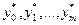 с координатой
с координатой 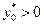 ; в противном случае задача (3.4.1) называется нерегулярной (вырожденной).
; в противном случае задача (3.4.1) называется нерегулярной (вырожденной).
Простейший класс регулярных задач получается из (3.4.1) при 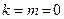 ; тогда допустимое множество задачи
; тогда допустимое множество задачи 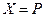 . В этом случае ограничения типа равенств и неравенств в (3.4.1) отсутствуют и нет необходимости вводить множители
. В этом случае ограничения типа равенств и неравенств в (3.4.1) отсутствуют и нет необходимости вводить множители 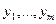 , поэтому
, поэтому 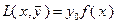 , условия (3.4.15) исчезают; кроме того, из утверждения теоремы 3.4.2 следует, что
, условия (3.4.15) исчезают; кроме того, из утверждения теоремы 3.4.2 следует, что 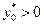 , тогда неравенство (3.4.14) превратится в условие
, тогда неравенство (3.4.14) превратится в условие 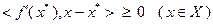 , известное из теоремы 3.3.4. Регулярность задачи (3.4.1) гарантируется также и в том случае, когда
, известное из теоремы 3.3.4. Регулярность задачи (3.4.1) гарантируется также и в том случае, когда 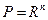 и градиенты
и градиенты 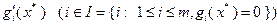 линейно независимы. Действительно, для пассивных ограничений
линейно независимы. Действительно, для пассивных ограничений 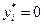 и условие (3.4.14) при
и условие (3.4.14) при 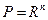 будет иметь вид
будет иметь вид
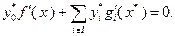
Если бы здесь было 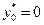 , то в силу линейной независимости
, то в силу линейной независимости 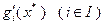 получили бы
получили бы 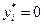 для всех
для всех 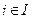 , но тогда
, но тогда 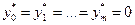 , что противоречит теореме 3.4.2.
, что противоречит теореме 3.4.2.
Из теоремы 3.4.2 следует, что в задаче (3.4.1) с гладкими функциями 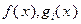 на выпуклом множестве
на выпуклом множестве 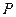 для поиска точек минимума (локального или глобального) нужно решить систему
для поиска точек минимума (локального или глобального) нужно решить систему
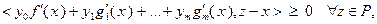 (3.4.16)
(3.4.16)
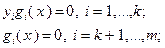 (3.4.17)
(3.4.17)
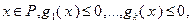
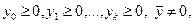 (3.4.18)
(3.4.18)
относительно 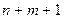 переменных
переменных 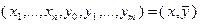 .
.
Если какие-либо 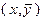 получены из системы (3.4.16) – (3.4.18), то
получены из системы (3.4.16) – (3.4.18), то 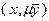 при любом
при любом 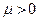 также удовлетворяют этой системе. Это значит, что множители Лагранжа из (3.4.16) – (3.4.18) определяются с точностью до постоянного положительного множителя. Поэтому множители Лагранжа можно подчинить какому-либо дополнительному условию нормировки, например, условию (3.4.8). В регулярной задаче вместо (3.4.18) можно взять
также удовлетворяют этой системе. Это значит, что множители Лагранжа из (3.4.16) – (3.4.18) определяются с точностью до постоянного положительного множителя. Поэтому множители Лагранжа можно подчинить какому-либо дополнительному условию нормировки, например, условию (3.4.8). В регулярной задаче вместо (3.4.18) можно взять 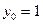 . Отсюда следует, что систему (3.4.16) – (3.4.18) достаточно исследовать для двух значений
. Отсюда следует, что систему (3.4.16) – (3.4.18) достаточно исследовать для двух значений 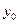 : при
: при 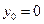 и при
и при 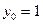 . Условия (3.4.16) – (3.4.18) вместе с условием нормировки (3.4.8) (или
. Условия (3.4.16) – (3.4.18) вместе с условием нормировки (3.4.8) (или 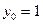 в регулярной задаче) дают «полную» систему соотношений для определения основных переменных
в регулярной задаче) дают «полную» систему соотношений для определения основных переменных 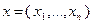 и соответствующих множителей Лагранжа
и соответствующих множителей Лагранжа 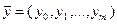 .
.
В регулярных задачах выпуклого программирования важную роль играет следующая теорема.
Теорема 3.4.3
Пусть задача (3.4.1) является задачей выпуклого программирования, функции 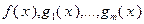 дифференцируемы на выпуклом множестве
дифференцируемы на выпуклом множестве 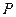 и пусть в точке
и пусть в точке 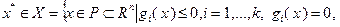
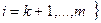 выполнены условия (3.4.14), (3.4.15) теоремы 3.4.2 с
выполнены условия (3.4.14), (3.4.15) теоремы 3.4.2 с 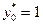 ,
, 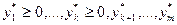 . Тогда точка
. Тогда точка 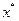 является глобальным решением рассматриваемой задачи выпуклого программирования.
является глобальным решением рассматриваемой задачи выпуклого программирования.
Доказательство. Поскольку рассматривается задача выпуклого программирования, функции 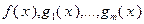 являются выпуклыми на множестве
являются выпуклыми на множестве 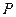 . В соответствии с (3.4.4), функция Лагранжа
. В соответствии с (3.4.4), функция Лагранжа 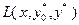 в данном случае имеет следующий вид:
в данном случае имеет следующий вид:
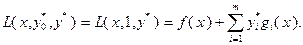 (3.4.19)
(3.4.19)
Согласно теореме 3.1.1, функция (3.4.19) является выпуклой на 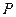 по переменной
по переменной 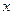 , так как функции
, так как функции 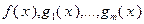 выпуклы на
выпуклы на 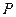 ,
, 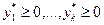 , функции
, функции 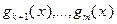 линейны и если при некотором
линейны и если при некотором 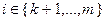 множитель
множитель 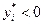 , то путем замены в (3.4.19) соответствующего слагаемого
, то путем замены в (3.4.19) соответствующего слагаемого 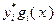 на
на 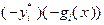 получаем произведение положительного множителя
получаем произведение положительного множителя 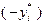 на функцию
на функцию 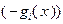 , являющуюся, как и
, являющуюся, как и 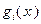 , линейной и, следовательно, выпуклой. Кроме того, в соответствии с условием теоремы,
, линейной и, следовательно, выпуклой. Кроме того, в соответствии с условием теоремы, 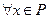 выполнено неравенство
выполнено неравенство 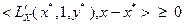 . Тогда по теореме 3.3.4 выпуклая функция (3.4.19) достигает минимума на множестве
. Тогда по теореме 3.3.4 выпуклая функция (3.4.19) достигает минимума на множестве 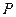 в точке
в точке 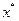 . Это означает, что
. Это означает, что 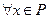 выполнено неравенство
выполнено неравенство 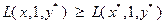 , которое можно записать в виде:
, которое можно записать в виде:
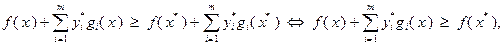 (3.4.20)
(3.4.20)
так как 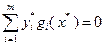 в силу выполнения условий (3.4.15). Поскольку
в силу выполнения условий (3.4.15). Поскольку 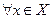 выполнены условия
выполнены условия 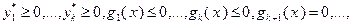
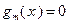 , то при этом будет также выполнено соотношение
, то при этом будет также выполнено соотношение
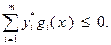
Тогда 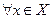 из (3.4.20) получаем:
из (3.4.20) получаем: 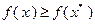 , т.е. точка
, т.е. точка 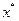 является глобальным решением рассматриваемой задачи выпуклого программирования. Теорема доказана.
является глобальным решением рассматриваемой задачи выпуклого программирования. Теорема доказана.
Важное место в теории выпуклого программирования занимает также следующая теорема (приводим только формулировку).
Теорема 3.4.4
Пусть в задаче (3.4.1) функции 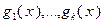 являются выпуклыми на выпуклом множестве
являются выпуклыми на выпуклом множестве 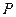 (
( 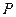 – полиэдр), а функции
– полиэдр), а функции 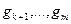 – линейными. Пусть точка
– линейными. Пусть точка 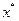 является решением задачи (3.4.1) в рассматриваемой постановке, функции
является решением задачи (3.4.1) в рассматриваемой постановке, функции 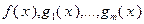 дифференцируемы на
дифференцируемы на 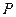 и выполнено одно из следующих условий:
и выполнено одно из следующих условий:
1) 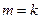 , т.е. имеем только ограничения типа неравенств, и
, т.е. имеем только ограничения типа неравенств, и 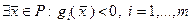 (условие Слейтера);
(условие Слейтера);
2) функции 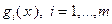 являются линейными.
являются линейными.
Тогда существуют числа 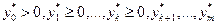 такие, что выполнены условия (3.4.14), (3.4.15).
такие, что выполнены условия (3.4.14), (3.4.15).
Таким образом, выполнение условий 1 или 2 теоремы 3.4.4 приводит к выполнению соотношений (3.4.14), (3.4.15) с 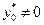 . Объединяя результаты, полученные в материале данного раздела, сформулируем теорему Куна-Таккера, известную также под названием теоремы о седловой точке функции Лагранжа.
. Объединяя результаты, полученные в материале данного раздела, сформулируем теорему Куна-Таккера, известную также под названием теоремы о седловой точке функции Лагранжа.
Теорема 3.4.5
Пусть рассматривается задача (3.4.1) и пусть она является задачей выпуклого программирования с ограничениями, удовлетворяющими условию 1 или условию 2 теоремы 3.4.4, а функции 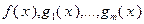 дифференцируемы на множестве
дифференцируемы на множестве 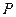 . Тогда условия (3.4.14), (3.4.15) с
. Тогда условия (3.4.14), (3.4.15) с 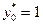 являются необходимыми и достаточными условиями оптимальности.
являются необходимыми и достаточными условиями оптимальности.
Дата добавления: 2021-05-28; просмотров: 416;











