Затруднения классической электронной теории электропроводности металлов.
Классическая теория смогла объяснить полученные ранее экспериментально законы Ома и Джоуля – Ленца, но есть и существенные затруднения. Основными являются следующие:
1. Теоретическое значение проводимости изменяется с температурой 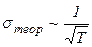 , экспериментальная же зависимость
, экспериментальная же зависимость 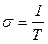 .
.
2. Классическая теория не в состоянии объяснить такое явление как сверхпроводимость.
Имеются и другие затруднения и в этом недостаточность классической теории.
Современная квантовая теория электропроводимости металлов показывает, что все трудности классической теории связаны с тем, что представление об электронах как идеальном газе является грубым приближением. На самом деле электроны внутри металла не являются такими свободными, как это следует из классической теории.
В современной квантовой теории показывается, что электроны внутри металла, как и электроны в атоме не могут иметь любую энергию, а лишь вполне дискретные значения энергии – энергия электронов квантуется.
Законы Кирхгофа
| 1. Первый закон Кирхгофа:
Алгебраическая сумма сил токов, сходящихся в узле, равна нулю.
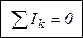 При этом токи, идущие к узлу, принято считать положительными, а от узла – отрицательными (можно и наоборот – это несущественно).
При этом токи, идущие к узлу, принято считать положительными, а от узла – отрицательными (можно и наоборот – это несущественно).
|
| Рис. 20.3 |
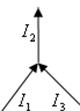
Заметим, что узел – это точка, где сходятся три и более тока. Например, для рис. 20.3 первый закон запишется так:
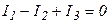 .
.
2. Второй закон Кирхгофа (он относится к любому выделенному в цепи замкнутому контуру):
Алгебраическая сумма произведений сил токов в отдельных участках произвольного замкнутого контура на их сопротивления (сумма падений напряжений) равна алгебраической сумме ЭДС, действующих в этом контуре.
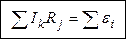
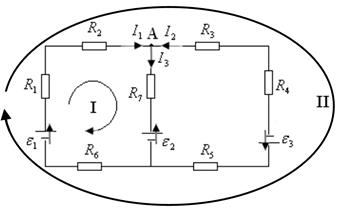
Применение этих законов рассмотрим на следующем примере. Дана электрическая цепь (рис. 20.4)
| Дано:
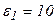 В, В, 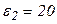 В, В, 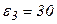 В, В,
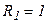 Ом, Ом, 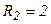 Ом…. Ом…. 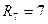 Ом.
Требуется найти токи Ом.
Требуется найти токи 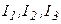 .
Для узла А составим уравнения по первому закону Кирхгофа: .
Для узла А составим уравнения по первому закону Кирхгофа:
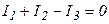 Для контура I запишем уравнение в соответствии со 2-ым законом Кирхгофа.
Для контура I запишем уравнение в соответствии со 2-ым законом Кирхгофа.
|
| Рис. 20.4 |
Причем падения напряжения и ЭДС берутся со знаком «+» если токи и ЭДС совпадают с направлением обхода (для контура I мы выбрали направление обхода «по часовой стрелке». Направление ЭДС указано на схеме стрелками 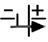 ). Таким образом:
). Таким образом:
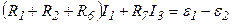
Пусть второй контур совпадает с внешним обходом цепи и направление обхода также по часовой стрелке. Тогда 2-ой закон Кирхгофа для контура II:
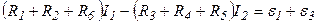
Итак, получили систему уравнений:
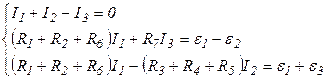
Решаем эту систему линейных уравнений с помощью определителей (метод Крамера).
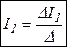
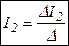
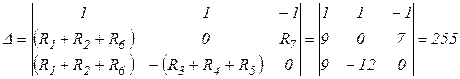 ,
,
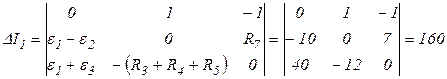 ,
,
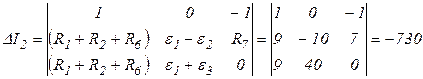 .
.
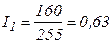 (А);
(А); 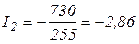 (А).
(А).
Далее используя 1-ый закон Кирхгофа, найдем 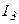 :
:
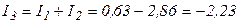 (А).
(А).
Отрицательные результаты означают, что на самом деле направление токов 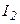 и
и 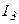 противоположно указанным на рис. 20.4.
противоположно указанным на рис. 20.4.
1.
Дата добавления: 2017-01-26; просмотров: 2661;











