Классификации картографических проекций

По характеру искажений проекции делятся на равноугольные, равновеликие и произвольные.

Равноугольные (или конформные) проекции сохраняют величину углов и формы бесконечно малых фигур. Масштаб длин в каждой точке постоянен по всем направлениям (что обеспечивается закономерным увеличением расстояний между соседними параллелями по меридиану) и зависит только от положения точки. Эллипсы искажений выражаются окружностями различных радиусов.

Для каждой точки в равноугольных проекциях справедливы зависимости:

/_Li = a = b = m = n; а>= 0°; 0= 90°; k = 1 и а₀=0° (или ±90°).

Такие проекции особенно удобны для определения направлений и прокладки маршрутов по заданному азимуту (например, при решении навигационных задач).

Равновеликие (или эквивалентные) проекции не искажают площади. В этих проекциях площади эллипсов искажений равны. Увеличение масштаба длин по одной оси эллипса искажений компенсируется уменьшением масштаба длин по другой оси, что вызывает закономерное уменьшение расстояний между соседними параллелями по меридиану и, как следствие, - сильное искажение форм.

Такие проекции удобны для измерения площадей объектов (что, например, существенно для некоторых экономических или морфометрических карт).

В теории математической картографии доказывается, что нет, и не может быть проекции, которая была бы одновременно и равноугольной, и равновеликой. Вообще, чем больше искажения углов, тем меньше искажения площадей и наоборот

Произвольные проекции искажают и углы, и площади. При их построении стремятся найти наиболее выгодное для каждого конкретного случая распределение искажений, достигая как бы некоторого компромисса. Эта группа проекций используется в случаях, когда чрезмерные искажения углов и площадей одинаково нежелательны. По своим свойствам произвольные проекции лежат между равноугольными и равновеликими. Среди них можно выделить равнопромежуточные (или эквидистантные) проекции, во всех точках которых масштаб по одному из главных направлений постоянен и равен главному.

Классификация картографических проекций по виду вспомогательной геометрической поверхности.

По виду вспомогательной геометрической поверхности различают проекции: цилиндрические, азимутальные и конические.

Цилиндрическиминазывают проекции, в которых сеть меридианов и параллелей с поверхности эллипсоида переносится на боковую поверхность касательного (или секущего) цилиндра, а затем цилиндр разрезается по образующей и развертывается в плоскость (рис. 6).

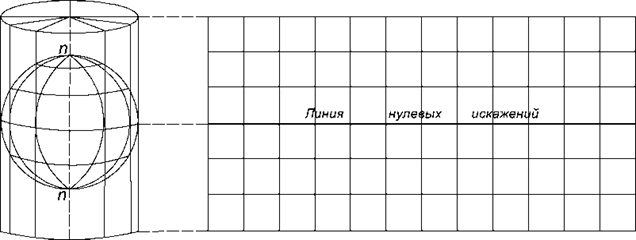
Рис.6. Нормальная цилиндрическая проекция

Искажения отсутствуют на линии касания и минимальны вблизи нее. Если цилиндр секущий, то имеется две линии касания, а значит 2 ЛНИ. Между ЛНИ искажения минимальны.

В зависимости от ориентировки цилиндра относительно оси земного эллипсоида различают проекции:

– нормальные, когда ось цилиндра совпадает с малой осью земного эллипсоида; меридианы в этом случае представляют собой равноотстоящие параллельные прямые, а параллели – прямые, им перпендикулярные линии;

– поперечные, когда ось цилиндра лежит в плоскости экватора; вид сетки: средний меридиан и экватор – взаимно перпендикулярные прямые, остальные меридианы и параллели – кривые линии (рис. в).

– косые, когда ось цилиндра составляет с осью эллипсоида острый угол; в косых цилиндрических проекциях меридианы и параллели – кривые линии.

Азимутальныминазывают проекции, в которых сеть меридианов и параллелей переносится с поверхности эллипсоида на касательную (или секущую) плоскость (рис.7).

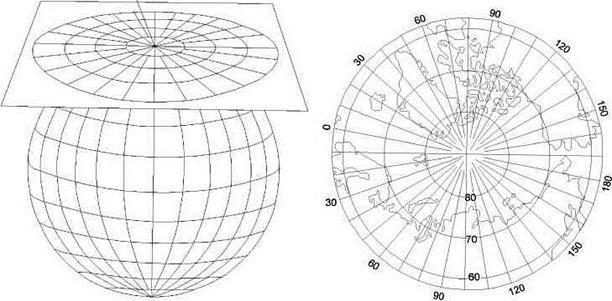
Рис. 7. Нормальная азимутальная проекция

Изображение около точки касания (или линии сечения) плоскости земного эллипсоида почти совсем не искажается. Точка касания является точкой нулевых искажений.

В зависимости от положения точки касания плоскости на поверхности земного эллипсоида среди азимутальных проекций различают:

– нормальные, или полярные, когда плоскость касается Земли в одном из полюсов; вид сетки: меридианы – прямые линии, радиально расходящиеся из полюса, параллели – концентрические окружности с центрами в полюсе (рис. 7);

– поперечные, или экваториальные, когда плоскость касается эллипсоида в одной из точек экватора; вид сетки: средний меридиан и экватор – взаимно перпендикулярные прямые, остальные меридианы и параллели – кривые линии (в некоторых случаях параллели изображаются прямыми линиями;

–косые, или горизонтные, когда плоскость касается эллипсоида в какой-либо точке, лежащей между полюсом и экватором. В косых проекциях только средний меридиан, на котором расположена точка касания, представляет собой прямую, остальные меридианы и параллели – кривые линии.

Коническиминазываются проекции, в которых сеть меридианов и параллелей с поверхности эллипсоида переносится на боковую поверхность касательного (или секущего) конуса (рис. 8).

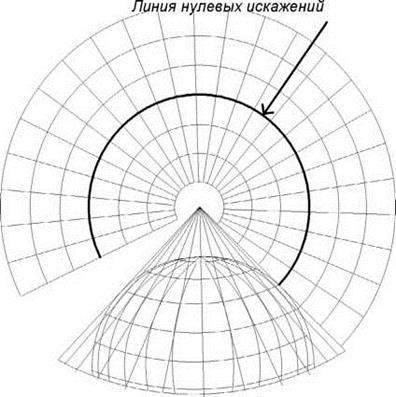
Рис. 8. Нормальная коническая проекция

Искажения мало ощутимы вдоль линии касания или двух линий сечения конуса земного эллипсоида, которые являются линией (линиями) нулевых искажений ЛНИ. Подобно цилиндрическим конические проекции делятся на:

– нормальные, когда ось конуса совпадает с малой осью земного эллипсоида; меридианы в этих проекциях представлены прямыми линиями, расходящимися из вершины конуса, а параллели – дугами концентрических окружностей.

– поперечные, когда ось конуса лежит в плоскости экватора; вид сетки: средний меридиан и параллель касания – взаимно перпендикулярные прямые, остальные меридианы и параллели – кривые линии;

– косые, когда ось конуса составляет с осью эллипсоида острый угол; в косых конических проекциях меридианы и параллели – кривые линии.

В нормальных цилиндрических, азимутальных и конических проекциях картографическая сетка ортогональна – меридианы и параллели пересекаются под прямыми углами, что является одним из важных диагностических признаков этих проекций.

Если при получении цилиндрических, азимутальных и конических проекций использовать геометрический метод (линейное проектирование вспомогательной поверхности на плоскость), то такие проекции называют перспективно-цилиндрическими, перспективно-азимутальными (обыкновенными перспективными) и перспективно-коническими соответственно.

Поликоническиминазываются проекции, в которых сеть меридианов и параллелей с поверхности эллипсоида переносится на боковые поверхности нескольких конусов, каждый из которых разрезается по образующей и развертывается в плоскость. В поликонических проекциях параллели изображаются дугами эксцентрических окружностей, центральный меридиан представляет собой прямую, все остальные меридианы – кривые линии, симметричные относительно центральному.

Условныминазываются проекции, при построении которых не прибегают к использованию вспомогательных геометрических поверхностей. Сеть меридианов и параллелей строят по какому-нибудь заранее заданному условию. Среди условных проекций можно выделитьпсевдоцилиндрические, псевдоазимутальные и псевдоконическиепроекции, сохраняющие от исходных цилиндрических, азимутальных и конических проекций вид параллелей. В этих проекцияхсредний меридиан – прямая линия, остальные меридианы – кривые линии.

К условным проекциям относятся также многогранные проекции, которые получают путем проектирования на поверхность многогранника, касающегося или секущего земной эллипсоид. Каждая грань представляет собой равнобочную трапецию (реже – шестиугольники, квадраты, ромбы). Разновидностью многогранных проекций являются многополосные проекции, причем полосы могут нарезаться и по меридианам, и по параллелям. Такие проекции выгодны тем, что искажения в пределах каждой грани или полосы совсем невелики, поэтому их всегда используют для многолистных карт. Основное неудобство многогранных проекций состоит в невозможности совмещения блока листов карт по общим рамкам без разрывов.

Практически ценным является подразделение по территориальному охвату. По территориальному охвату выделяются картографические проекции для карт мира, полушарий, материков и океанов, карт отдельных государств и их частей. По этому принципу построены таблицы-определители картографических проекций. Кроме того, в последнее время предпринимаются попытки к разработке генетических классификаций картографических проекций, построенных на виде описывающих их дифференциальных уравнений. Эти классификации охватывают все возможное множество проекций, но являются крайне ненаглядными, т.к. не связаны с видом сетки меридианов и параллелей.