ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ВЗАИМОДЕЙСТВИЯ
Рассмотрим систему из двух взаимодействующих частиц. Ограничимся весьма распространенным случаем, когда силы, с которыми частицы действуют друг на друга, направлены вдоль прямой соединяющей частицы, а их величина зависит только от расстояния между частицами.
Если считать, что первая частица находится в начале координат (т.е. если поместить начало координат в точку, где находится первая частица), то вторую можно считать находящейся в центральном поле, созданном первой, поскольку она находится в условиях, соответствующих определению центрального поля. Силы этого поля являются консервативными, поэтому можно утверждать, что вторая частица обладает потенциальной энергией 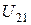 в поле созданном первой.
в поле созданном первой.
Частицы абсолютно равноправны. Поэтому, считая вторую находящейся в начале координат, можем утверждать, что в центральном потенциальном поле, созданном второй частицей, первая обладает потенциальной энергией 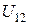 .
.
В силу полной симметрии задачи относительно частиц, можно утверждать, что
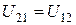 (3.39)
(3.39)
Для определенности условимся считать, что в начале координат находится первая частица. Положение второй можно характеризовать радиус-вектором 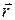 , проведенным к ней из начала координат. Тогда для силы, действующей на вторую частицу можно записать выражение:
, проведенным к ней из начала координат. Тогда для силы, действующей на вторую частицу можно записать выражение:
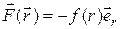 (3.40)
(3.40)
где 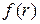 – функция расстояния до второй частицы, которая принимает:
– функция расстояния до второй частицы, которая принимает:
– положительные значения в случае притяжения частиц,
– отрицательные значения в случае отталкивания частиц.
(Вектор 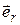 направлен в сторону отталкивания частиц. Поэтому при притяжении частиц знак «минус» «поворачивает» вектор
направлен в сторону отталкивания частиц. Поэтому при притяжении частиц знак «минус» «поворачивает» вектор 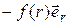 к первой частице. А при отталкивании отрицательная
к первой частице. А при отталкивании отрицательная 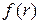 дает при умножении на «минус» положительные значения.)
дает при умножении на «минус» положительные значения.)
Чтобы найти выражение для потенциальной энергии второй частицы в поле, созданном первой, найдем работу 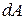 , совершаемую силами поля при перемещении второй частицы на
, совершаемую силами поля при перемещении второй частицы на 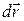 . По определению потенциальной энергии,
. По определению потенциальной энергии, 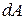 равна убыли
равна убыли 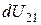 , поскольку работа совершается за счет уменьшения потенциальной энергии:
, поскольку работа совершается за счет уменьшения потенциальной энергии:
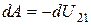 . (3.41)
. (3.41)
П определению механической работы
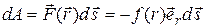 . (3.42)
. (3.42)
Но скалярное произведение 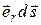 можно рассматривать как проекцию приращения
можно рассматривать как проекцию приращения 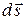
на направление орта 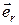 , которая равна приращению расстояния между частицами
, которая равна приращению расстояния между частицами
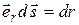 . (3.43)
. (3.43)
Следовательно
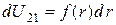 . (3.44)
. (3.44)
Интегрируя соотношение (3.44), можно найти выражение для потенциальной энергии второй частицы по известной функции 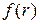 .
.
Эта функция может иметь различный вид в конкретных задачах, однако наибольший практический интерес представляет случай, когда она имеет вид:
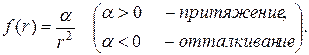 (3.45)
(3.45)
(Вспомните закон всемирного тяготения или закон Кулона – 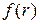 вида (3.45) охватывает и один и другой. )
вида (3.45) охватывает и один и другой. )
В этом конкретном случае (т.е. при выполнении соотношения (3.45))
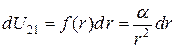 . (3.46)
. (3.46)
Интегрируя (3.46), найдем:
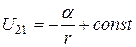 . (3.47)
. (3.47)
Как и следовало ожидать, потенциальная энергия 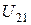 оказалась определенной с точностью до произвольной константы интегрирования.
оказалась определенной с точностью до произвольной константы интегрирования.
Рассуждая аналогичным образом, но поместив начало координат в точку, где находится вторая частица, для потенциальной энергии 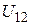 первой частицы в поле, созданном второй, можем получить соотношение, симметричное (3.46):
первой частицы в поле, созданном второй, можем получить соотношение, симметричное (3.46):
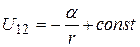 . (3.48)
. (3.48)
Это вполне естественный вывод: ведь, по сути дела, речь идет об одной и той же энергии – энергии взаимодействия частиц 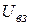 . Поскольку частицы абсолютно равноправны, то выражение для энергии взаимодействия принято записывать в симметричном виде:
. Поскольку частицы абсолютно равноправны, то выражение для энергии взаимодействия принято записывать в симметричном виде:
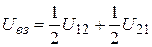 . (3.49)
. (3.49)
Можно доказать, что потенциальная энергия взаимодействия системы из 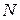
частиц, между которыми действуют только консервативные силы, равна полусумме энергий попарных взаимодействий:
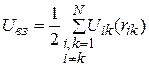 . (3.49)
. (3.49)
Эта энергия зависит только от взаимного расположения частиц – 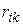 – другими словами от конфигурации системы. Если конфигурация не изменяется, то
– другими словами от конфигурации системы. Если конфигурация не изменяется, то 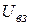 остается постоянной, т.е. внутренние силы работы не совершают.
остается постоянной, т.е. внутренние силы работы не совершают.
Отметим, что, рассматривая сплошное (не абсолютно твердое, а упруго деформируемое) тело, как систему взаимодействующих частиц, можно рассматривать потенциальную энергию упругой деформации как энергию взаимодействия образующих тело частиц.
Дата добавления: 2017-01-26; просмотров: 1928;











