ПОЛНАЯ МЕХАНИЧЕСКАЯ ЭНЕРГИЯ
Как мы установили ранее (см. соотношение (3.10)), работа результирующей силы, действующей на частицу, идет на приращение ее кинетической энергии. Если на частицу действуют только консервативные силы, то их работа равна по формуле (3.22) равна убыли потенциальной энергии ( 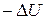 ) и идет на приращение кинетической энергии частицы:
) и идет на приращение кинетической энергии частицы:
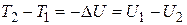 . (3.24)
. (3.24)
Перегруппируем члены в соотношении (3.24) по индексам следующим образом:
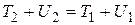 . (3.25)
. (3.25)
Формула (3.25) означает, что в отсутствие неконсервативных сил величина
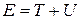 (3.26)
(3.26)
не изменяется при движении частицы, а значит, является интегралом движения. Эту величину называют полной механической энергией частицы.
Если рассматриваемая система состоит из N невзаимодействующих частиц, находящихся в поле консервативных сил, то полная энергия системы 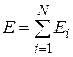 также является интегралом движения. Действительно, для каждой частицы справедливо соотношение (3.23), поэтому
также является интегралом движения. Действительно, для каждой частицы справедливо соотношение (3.23), поэтому
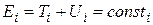 (3.27)
(3.27)
Тогда
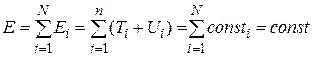 (3.28)
(3.28)
Однако полная энергия сохраняется не всегда. Рассмотрим ситуацию, когда на частицу кроме консервативных 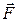 действует неконсервативная сила
действует неконсервативная сила 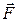 *. При переходе из точки 1 в 2 над частицей совершается работа:
*. При переходе из точки 1 в 2 над частицей совершается работа:
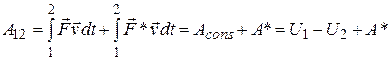 (3.29)
(3.29)
Поскольку суммарная работа всех сил идет на приращение кинетической энергии, то можно записать
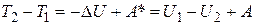 . (3.30)
. (3.30)
Группируя в (3.30) слагаемые, получаем:
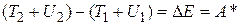 . (3.31)
. (3.31)
А это означает, что работа неконсервативных сил равна приращению полной механической энергии частицы.
Типичными неконсервативными являются силы трения и сопротивления среды. Работа этих сил, как правило, отрицательна, поскольку они направлены противоположно перемещению. Поэтому действие этих сил обычно приводит к убыли (ΔЕ < 0) полной энергии за счет её перехода во внутреннюю энергию тел. Этот процесс называется диссипацией энергии, а соответственно силы, обеспечивающие ее, – диссипативными.
Дата добавления: 2017-01-26; просмотров: 1516;











