Динамика ведомого колеса.

При качении жесткого колеса по недеформируемой поверхности (идеальный случай) на колесо действует нагрузка G_к, толкающая сила Р, реакция дороги N, нормальная к поверхности контакта и уравновешивающая нагрузку G_к, а также сила трения между колесом и дорогой μN. Кроме того, в подшипнике колеса возникает момент трения М_r (рис. 2-а). В этом случае сила трения относительно оси колеса равна толкающей силе, а момент силы трения относительно оси колеса равен моменту трения в его подшипнике.

В действительности колесо и опорная поверхность деформируются. При этом точка приложения результирующей реакции контакта смещается в направлении движения на величину а. Эта величина характеризует коэффициент трения качения. На рис.2-б показано движение колеса при небольшой деформации колеса и дороги в зоне контакта. Результирующая сила Z реакций, нормальных к поверхности дороги, смещается вперед на величину а (плечо трения качения). Ее горизонтальная компонента Х является толкающей силой.

Уравнение моментов сил относительно оси колеса найдется как:

Z ·а + М_r = Х·r₁

В рассматриваемом случае изменение радиуса колеса r₁ в связи с малой деформацией можно пренебречь. Толкающая сила Х, необходимая для качения колеса, равна:

Х = (Z ·а + М_r) / r₁ .

Если пренебречь небольшим моментом трения в подшипнике колеса, имеем:

Х = (Z ·а) / r₁ .

Отношение толкающей силы к нагрузке характеризует сопротивление качению и называется коэффициентом сопротивления качению:

Х / Z = f = а / r₁. Х = f·Z .

Из приведенных выражений видно, что с увеличением радиуса колеса r₁ сопротивление качению уменьшается.

При качении жесткого колеса (идеальный случай) по мягкому грунту под влиянием нагрузки G_к и толкающей силы Р возникают деформации смятия и сдвига почвы с образованием колеи (рис.2-в,г). Нормальная сила реакции почвы N и сил трения μN между колесом и дорогой расположены по вертикале на расстоянии (r₁ ·cos α) от оси колеса. Результирующую силу R (геометрическая сумма сил N и μN) разложим на две составляющие: нормальную к плоскости дороги и перпендикулярную ей (параллельную плоскости дороги) Х (рис.2-г).

При этом уравнение моментов относительно оси вращения колеса запишется как:

Z·а + М_r = Х· r₁ ·cos α.

Из рис.2-г видно, что реакция дороги Х = Р, а нагрузка на колесо уравновешивается реакцией Z , т.е. G_к = Z.

Пренебрегая трением в подшипнике колеса, имеем:

Р·r₁·cos α = Z·а, или

Р·r₁·cos α = G_к ·а.

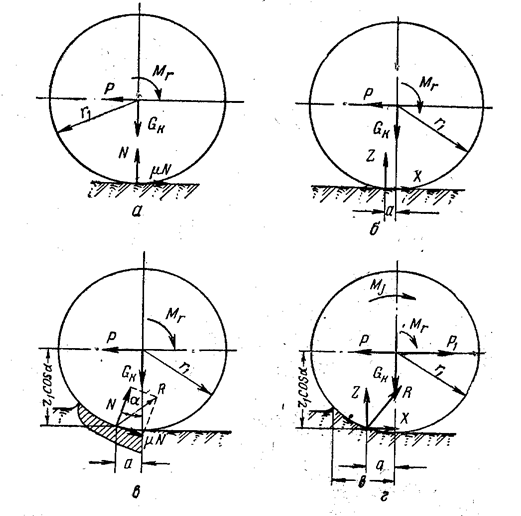Рис.2. Силы и моменты, действующие на ведомое колесо.

Произведение G_к·а представляет собой момент сопротивления качению М_f1. Отсюда толкающая сила Р равна:

Р = М_f1/(r₁·cos α).

Отношение плеча трения качения а к расстоянию от точки приложения толкающей силы Р до точки приложения реакции дороги по вертикали (r₁·cos α ) называется коэффициентом сопротивления качению. Из приведенных выше соотношений нетрудно установить, что:

f = а /(r₁·cos α) .

При ускоренном движении машины к оси колеса дополнительно будет приложена сила инерции движущихся масс Р_j и момент касательных сил инерции вращающихся масс М_j. В этом случае толкающая сила определится как:

Р = (М_f1 + М_r + М_j ) / ( r₁·cos α) + Р_j.

При качении эластичного (деформированного) колеса под действием силовых факторов действительное расстояние от оси вращения колеса до опорной поверхности уменьшается и становится равным r_д. Это расстояние называют динамическим радиусом колеса. Его величина зависит от ряда конструктивных и эксплуатационных факторов, таких, например, как жесткость шины и внутреннее давление в ней, вес автомобиля, приходящейся на колесо, скорость движения, ускорение, сопротивление качению и др.

С учетом динамического радиуса для случая ускоренного движения автомобиля зависимость силы Р имеет следующий вид:

Р = (М_f1 + М_r + М_j ) / ( r_д) + Р_j.

Качение эластичного колеса по твердой опорной поверхности (например, по асфальтовому или бетонному шоссе) сопровождается некоторым проскальзыванием элементов протектора колеса в зоне его контакта с дорогой. Это объясняется разностью длин участков колеса и дороги, вступающих в контакт. Проскальзывания не было бы при условии абсолютного равенства этих участков. Но это возможно лишь в том случае, когда колесо и дорога имеют контакт по дуге. В действительности же, опорный контур деформированного колеса вступает в контакт с плоской поверхностью недеформированной дороги, и проскальзывание становится неизбежным.

Для учета этого явления в расчетах используют понятие кинематического радиуса колеса (радиуса качения) r_к. Физическое определение r_к и методика расчета его величины приведены выше. Заметим лишь, что r_к - это условный радиус, который служит для выражения расчетной кинематической зависимости между скоростью движения v автомобиля и угловой скоростью вращения колеса ω_к:

r_к = v / ω_к .

Величина проскальзывания растет при одновременном увеличении эластичности (податливости) шины и жесткости дороги или, наоборот, при увеличении жесткости шины и мягкости дороги. На мягкой грунтовой дороге повышенное давление в шине увеличивает потери на деформацию грунта. Снижение внутреннего давления в шине позволяет на мягких грунтах уменьшить перемещение частиц почвы и деформации ее слоев, что обуславливает снижение сопротивления качению и повышению проходимости.

Однако, на твердой опорной поверхности при малом давлении происходит чрезмерный прогиб шин с увеличением плеча трения качения а. Компромиссным решение данной проблемы является использование шин с регулируемым внутренним давлением.