Расчет индуктивных датчиков перемещений

Целью расчета индуктивного измерительного преобразователя является определение его конструктивных параметров по заданным метрологическим характеристикам или расчет метрологических ха­рактеристик данной конструкции индуктивного измерительного пре­образователя.

Эти расчеты связаны с теорией электромагнитных це­пей. Основными метрологическими характеристиками индуктивного измерительного преобразователя являются:

1) диапазон измерения с допустимой погрешностью ;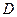

2) чувствительность преобразования (относительная) ;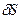

3) погрешность преобразования (относительная) .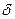

В качестве конструктивных параметров индуктивного преобра­зователя, определяющих его метрологические характеристики, не­обходимо учитывать геометрические размеры магнитопровода и его материал, геометрические размеры и число витков катушки преоб­разователя.

С точки зрения расчета индуктивные измерительные преобразо­ватели можно разделить на три вида: преобразователи с переменной длиной немагнитных зазоров в магнитопроводе, преобразователи с переменной площадью немагнитных зазоров в магнитопроводе и соленоидные преобра­зователи.

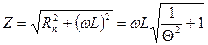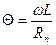Выходной величиной индуктивного измерительного преобразователя является его полное сопротивление, модуль которого определяется зависимостью , где – добротность преобразователя.

Индуктивность преобразователя 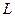в первую очередь зависит от конструктивных параметров преобразователя и электромагнитных характеристик его элементов (в рабочем диапазоне частот). Величины 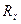и существенно зависят ещё и от режима работы преобразователя и, в частности, от частоты 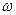. В связи с этим модуль полного сопротивления преобразователя будет определенной величиной только для фиксированного режима работы преобразователя.

С другой стороны, характерной особенностью добротности 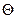является слабая зависимость этой величины (в рабочем диапазоне режимов преобразователя) от режима работы преобразователя и входной величины.

Приведенные рассуждения показывают целесообразность применения для характеристики индуктивного измерительного преобразователя двух достаточно стабильных величин 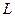и .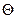

При этом с небольшой погрешностью результата в практических случаях можно принять и вместо зависимости 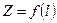рассматривать зависимость , приняв последнюю в качестве функции преобразования индуктивного измерительного преобразователя.

Применяемые методы расчета индуктивных преобразователей базируются на теории магнитных цепей с зазорами. Исходными являются следующие расчетные соотношения: магнитный поток в магнитопрово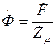де , где 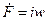– намагничивающая сила обмотки преобразователя, 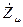– магнитное комплексное сопротивление магнитопроводов и зазоров;

индуктивность преобразователя 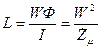, где 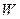– число витков обмотки преобразователя.

Решение задачи сводится к определению магнитного сопротивления магнитной цепи. Последнее складывается из магнитного сопротивления ферромагнитных и немагнитных участков цепи 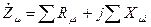, где 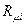, 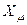– полное активное магнитное сопротивление и полное реактивное магнитное сопротивление.

Для нахождения 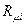и 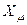предлагаются следующие соотношения:

; ,

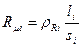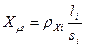где 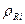, 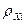– удельное активное и реактивное магнитные сопротивления, 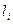, 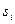– длина и площадь сечения однородных участков магнитопровода.

Удельное активное сопротивление 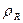учитывает магнитные свойства вещества магнитопровода и определяется из соотношения

.

Удельное реактивное магнитное сопротивление учитывает потери в магнитопроводе, в первую очередь от вихревых токов, в значительной мере определяется не только материалом магнитопровода, но и его конструкцией. При слабо выраженном поверхностном эффекте в магнитопроводе преобразователя допустимо при расчете принимать 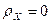. С учетом сказанного при практических расчетах часто принимают

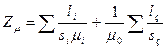, где 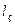, – длина и площадь сечения немагнитных зазоров.