Определение предела функции одной переменной по Коши. Замечательные пределы.
Определение 3.4.Говорим, что 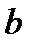 является пределом функции
является пределом функции 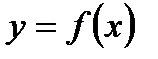 при
при 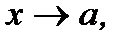 если для произвольного заранее взятого положительного числа
если для произвольного заранее взятого положительного числа 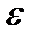 существует зависящего от
существует зависящего от 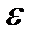 такое положительное число
такое положительное число 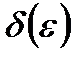 , что из неравенства
, что из неравенства 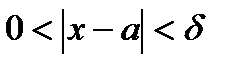 следует неравенство
следует неравенство 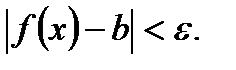
На языке символики определение 3.4 имеет вид:
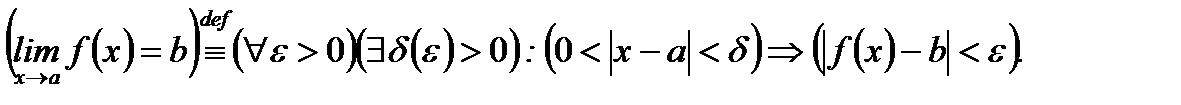 (3.1)
(3.1)
Если раскрыть знаки модулей в (3.1), то получим
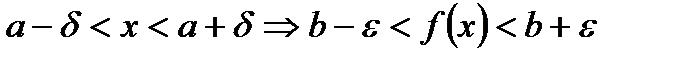 . (3.2)
. (3.2)
Последние неравенства показывают, что 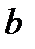 есть предел
есть предел 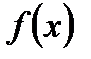 при
при 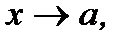 если выполняется условие: когда значения
если выполняется условие: когда значения 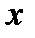 попадают в
попадают в 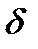 окрестность точки
окрестность точки 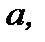 значения функции должны попасть в
значения функции должны попасть в 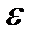 окрестность точки
окрестность точки 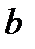 (рис. 3.5).
(рис. 3.5).
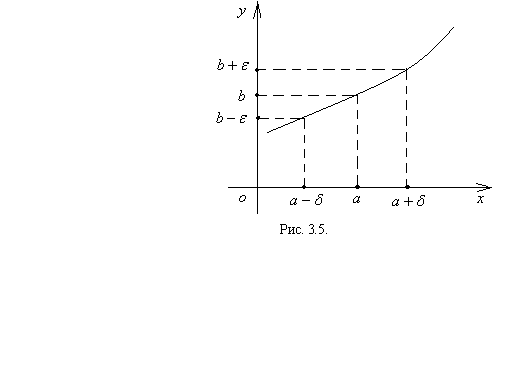
Отметим, что основой теории пределов функций одной независимой переменной являются два замечательных предела. Ниже приведем их без доказательства.
Первый замечательный предел – 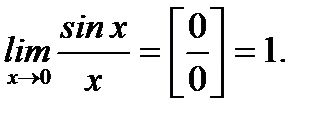 (3.3)
(3.3)
Второй замечательный предел – 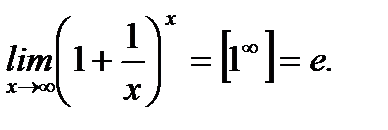 (3.4)
(3.4)
Заметим, что эти пределы инварианты (остаются неизменными) относительно аргумента, то есть
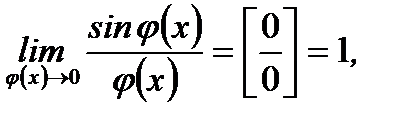
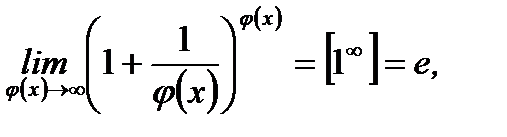
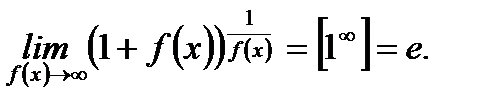 (3.5)
(3.5)
Отметим также, что вычисление пределов основывается на следующих свойствах:
1. 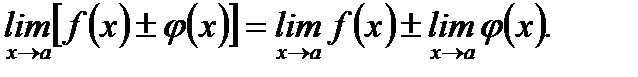 2.
2. 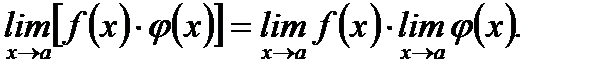 (3.6)
(3.6)
3. 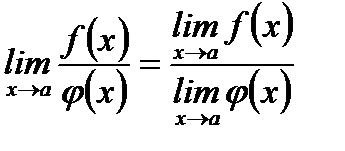 (если
(если 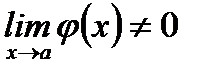 ).
).
4. 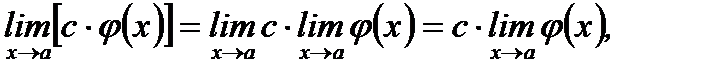 где
где 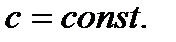
При вычислении предела пункта 4 учли, что предел от постоянного числа  равен самому
равен самому
числу  . Свойство пункта 4 показывает, что постоянный множитель можно вынести из
. Свойство пункта 4 показывает, что постоянный множитель можно вынести из
под знака предела.
Дата добавления: 2021-05-28; просмотров: 580;











