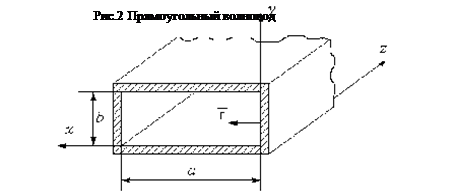
Прямоугольный волновод. Магнитные волны.
Волновое уравнение для 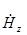 имеет вид:
имеет вид:
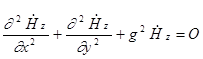
Сравним это уравнение с уравнением в разделе электрические волны. Они одинаковы, следовательно, общее решение этого уравнения аналогично. Запишем это решение:
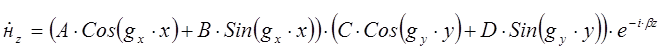
Запишем граничные условия для данного уравнения. На границе с идеальным проводником касательная составляющая магнитного поля достигает экстремума, следовательно:
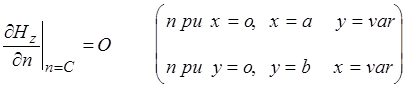 , где
, где
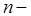 нормаль к внутренней поверхности волновода
нормаль к внутренней поверхности волновода
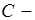 контур волновода в поперечном сечении.
контур волновода в поперечном сечении.
 |
Теперь будем искать 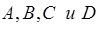 из данных граничных условий:
из данных граничных условий:
1) 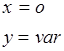
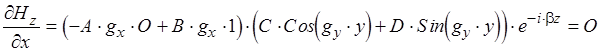
Отсюда 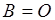
2) 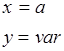
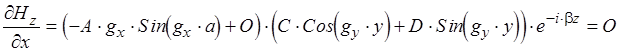 для этого
для этого 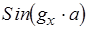 должно
должно 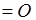 . Тогда
. Тогда 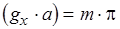 , где
, где 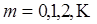 Отсюда
Отсюда 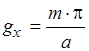
3) 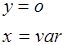
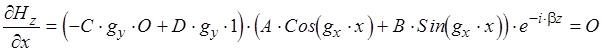
Отсюда 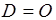
4) 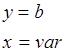
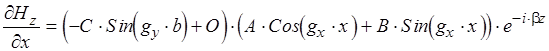
для этого 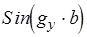 должно
должно 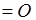 . Тогда
. Тогда 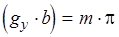 , где
, где 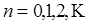 Отсюда
Отсюда 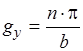
Приведём окончательное выражение для 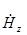 Величины
Величины 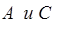 определяются мощностью источника электромагнитной энергии.
определяются мощностью источника электромагнитной энергии. 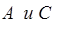 нельзя определить из граничных условий, поэтому сделаем обозначение :
нельзя определить из граничных условий, поэтому сделаем обозначение :
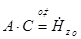
C учётом этого получим:
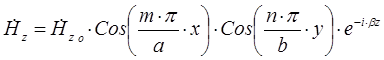
Где 
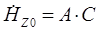 - амплитуда продольной составляющей магнитного поля.
- амплитуда продольной составляющей магнитного поля.
Получим поперечные составляющие электромагнитного поля на основании формулы 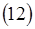 и формул
и формул 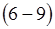 :
:
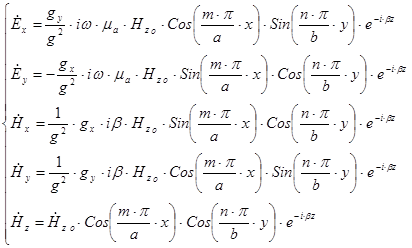
Данная система позволяет описать поле волны для 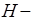 волн.
волн.
У волн Н в отличие от волн Е обращение в нуль одного из индексов (m или n) не влечет за собой обращение в нуль всех составляющих поля. Поэтому, если полагать, что a > b, то низшим типом волн сред и волн Н является волна H10, у которой 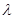 кр = 2а
кр = 2а
Критическая длина волны по аналогии с 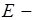 волной найдётся по формуле:
волной найдётся по формуле:
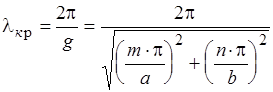
Исследуем все полученные зависимости: в данном случае допустимо, чтобы 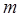 или
или 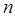 были равны нулю. Тогда поле не меняется по одной из координат. Однако если
были равны нулю. Тогда поле не меняется по одной из координат. Однако если 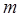 и
и 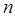 будут равны нулю одновременно, то
будут равны нулю одновременно, то 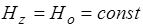 в поперечном сечении, что приводит к нулевым поперечным составляющим, т. е. свидетельствует об отсутствии электромагнитной волны. Следовательно, простейшие волны этого класса с минимальными индексами:
в поперечном сечении, что приводит к нулевым поперечным составляющим, т. е. свидетельствует об отсутствии электромагнитной волны. Следовательно, простейшие волны этого класса с минимальными индексами: 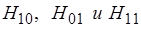
Волну, обладающую в волноводе данной формы минимальной критической частотой, называют основной. Если для волновода выполняется условие, что 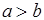 то низшим типом волны будет являться волна
то низшим типом волны будет являться волна 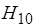 . Эта волна имеет низший тип не только среди магнитных, но и среди электрических волн, поскольку у неё критическая длина волны самая большая:
. Эта волна имеет низший тип не только среди магнитных, но и среди электрических волн, поскольку у неё критическая длина волны самая большая:

Это означает, что если l > 2а, то передача энергии по прямоугольному волноводу не возможна.
Коэффициент распространения, фазовая скорость, групповая скорость, волновое сопротивление волн Emn или Нmn определяется по ранее приведенным формулам.
 |
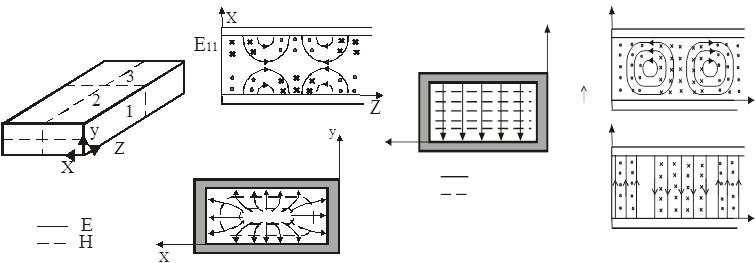
На рис.3 представлены структура волн Е11 и Н10 в некоторый фиксированный момент времени.
Наиболее широкое распространение в технике сверхвысоких частот находит волна Н10. Она имеет наибольшую критическую длину. Поэтому на заданной частоте размеры поперечного сечения волновода, при которых возможна передача энергии по прямоугольному волноводу, для этой волны наименьшие и, следовательно, меньше все габариты волновода, ниже его стоимость. Полагая, что m = 1 и n = 0, получаем выражение, составляющих поля волны.
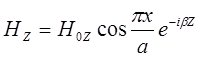
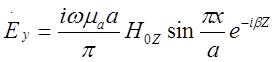
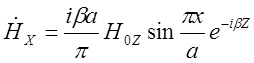
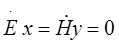
Основные параметры волны Н10 определяются по формуле:
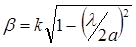 ;
; 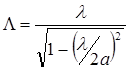 ;
; 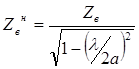
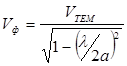 ;
; 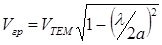
Дата добавления: 2017-01-16; просмотров: 2621;











