Прямоугольный волновод. Электрические волны.
Решение граничной задачи для E - волн ( 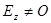 ,
, 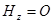 ) должно удовлетворять волновому уравнению для составляющей
) должно удовлетворять волновому уравнению для составляющей 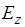 и граничным условиям на стенках волновода (считаем их идеально проводящими). Волновое уравнение в декартовой системе координат выглядит так:
и граничным условиям на стенках волновода (считаем их идеально проводящими). Волновое уравнение в декартовой системе координат выглядит так:
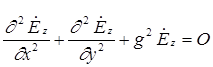 |
Решение уравнения произведём с помощью метода разделения переменных, искомая функция представляется в виде произведения двух функций, каждая из которых зависит от одного аргумента.
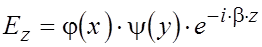 (1)
(1)
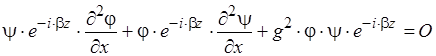
Помножим данное уравнение на 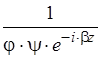
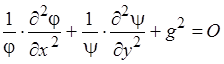
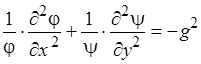
Перейдём к двум уравнениям, зависящим только от одной переменной:
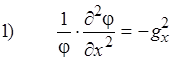
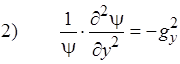
Преобразуем:
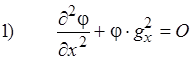
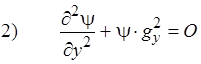
Оба эти уравнения принципиально одинаковы, а, следовательно, общее решение этих уравнений одинаково:
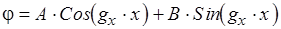
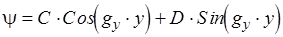
где 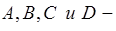 постоянные интегрирования. Подставим эти уравнения в уравнение (1).
постоянные интегрирования. Подставим эти уравнения в уравнение (1).
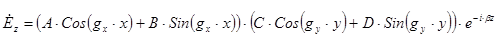
Продольная составляющая поля 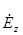 является касательной к поверхности стенок волновода. На границе с идеальным проводником касательная составляющая электрического поля равна нулю, следовательно:
является касательной к поверхности стенок волновода. На границе с идеальным проводником касательная составляющая электрического поля равна нулю, следовательно:
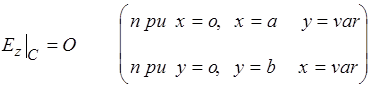
где 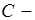 контур волновода в поперечном сечении.
контур волновода в поперечном сечении.
Теперь будем искать 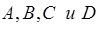 из данных граничных условий:
из данных граничных условий:
1) 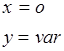
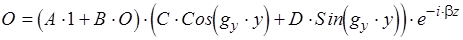
Отсюда 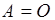
2) 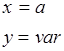
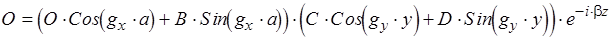 для этого
для этого 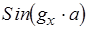 должно
должно 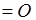 . Тогда
. Тогда 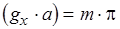 , где
, где 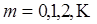 Отсюда
Отсюда 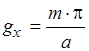
3) 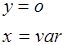
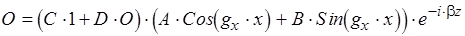
Отсюда 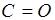
4) 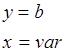
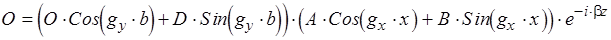 для этого
для этого 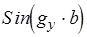 должно
должно 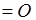 . Тогда
. Тогда 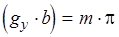 , где
, где 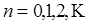 Отсюда
Отсюда 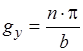
Приведём окончательное выражение для 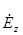 Величины
Величины 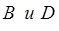 определяются мощностью источника электромагнитной энергии.
определяются мощностью источника электромагнитной энергии. 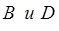 нельзя определить из граничных условий, поэтому сделаем обозначение :
нельзя определить из граничных условий, поэтому сделаем обозначение :
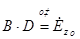
C учётом этого получим:
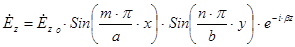 (2)
(2)
Исследуем полученное выражение. Можно заметить, что при 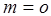 , а так же при
, а так же при 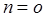
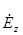 будет всегда
будет всегда 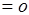 . А если
. А если 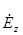
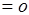 то такое поле нельзя назвать электрическим. Поэтому
то такое поле нельзя назвать электрическим. Поэтому 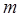 и
и 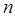 не могут быть нулевыми, а начинаются с единицы.
не могут быть нулевыми, а начинаются с единицы.
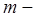 показывает, сколько полуволн укладывается в волноводе по направлению оси
показывает, сколько полуволн укладывается в волноводе по направлению оси 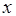 .
.
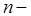 показывает, сколько полуволн укладывается в волноводе по направлению оси
показывает, сколько полуволн укладывается в волноводе по направлению оси 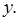
В связи с вышеизложенным электрические волны принято обозначать, как 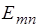 . Наименьший тип волн
. Наименьший тип волн 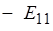
Получим поперечные составляющие электромагнитного поля на основании формулы (2) и формул 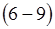 :
:
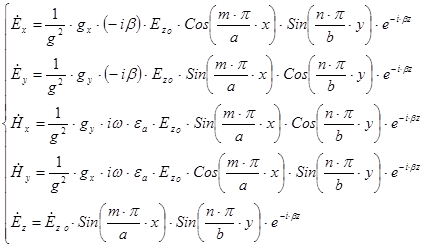
Данная система позволяет описать поле волны для 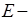 волн.
волн.
Теперь найдём критическую длину 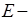 волны для данного прямоугольного волновода:
волны для данного прямоугольного волновода:
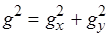 ;
; 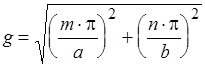
Отсюда:
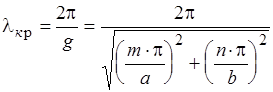
Дата добавления: 2017-01-16; просмотров: 2282;











