Выбор размеров поперечного сечения волновода.
Размеры поперечного сечения нужно выбирать такими, чтобы волновод обеспечивал :
1) Обеспечение одномодового режима передачи электромагнитной энергии.
2) Снижение напряжённости электрического поля.
3) Уменьшение затухания.
4) Использование волновода, имеющего минимальные размеры и массу.
Волна 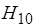 по сравнению с другими волнами обеспечивает более низкое затухание и наименьшие геометрические размеры.
по сравнению с другими волнами обеспечивает более низкое затухание и наименьшие геометрические размеры.
Найдём размеры волновода, обеспечивающие передачу волны типа 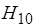 с приемлемыми параметрами и отсечку всех волн высших порядков. Для такого волновода должно выполняться условие:
с приемлемыми параметрами и отсечку всех волн высших порядков. Для такого волновода должно выполняться условие:
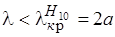
Ближайшими типами волн к 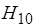 являются волны
являются волны 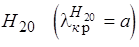 и
и 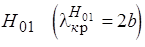 . Чтоб исключить возможность передачи этих типов волн нужно выполнить следующие два условия:
. Чтоб исключить возможность передачи этих типов волн нужно выполнить следующие два условия:
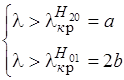
Отсюда:
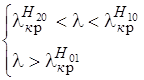
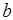 по отношению к
по отношению к 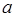 можно выбрать сколь угодно малой толщины. Но с уменьшением
можно выбрать сколь угодно малой толщины. Но с уменьшением 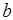 возрастает напряжённость электрического поля внутри волновода и растёт затухание. Поэтому на практике обычно используют следующее соотношение
возрастает напряжённость электрического поля внутри волновода и растёт затухание. Поэтому на практике обычно используют следующее соотношение 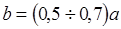 .
.
| Тип волны | а=11 мм; в=5.5 мм | а=48 мм; в=24 мм | ||
| lкр, мм | fкр, МГц | lкр, мм | fкр, МГц | |
| H10 | 22.0 | 96.0 | ||
| H20 | 11.0 | 48.0 | ||
| H30 | 7.3 | 32.0 | ||
| H01 | 11.0 | 48.0 | ||
| H02 | 5.5 | 24.0 | ||
| H11, E11 | 9.8 | 42.8 | ||
| H12, E12 | 5.3 | 23.3 |
4.2.5. Цилиндрические металлические волноводы
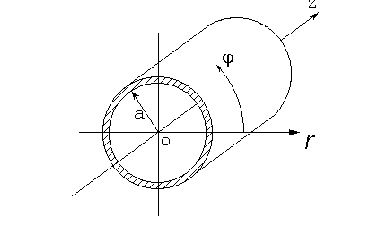 |
Рассмотрим металлический волновод, стенки которого представляют круговой цилиндр (рис.6).
|
Электрические волны ( 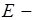 волны)
волны)
Волновое уравнение для продольной составляющей 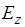 записывается в цилиндрической системе координат следующим образом:
записывается в цилиндрической системе координат следующим образом:
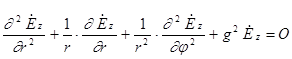
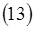
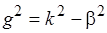
Рассматриваем идеальный случай (без потерь). Решим данное уравнение и определим 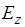 . Для решения воспользуемся методом разделения переменных:
. Для решения воспользуемся методом разделения переменных:
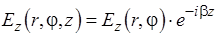 , где
, где
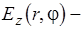 отвечает за изменения
отвечает за изменения 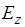 в поперечном направлении;
в поперечном направлении;
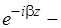 отвечает за изменения
отвечает за изменения 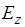 в поперечном направлении.
в поперечном направлении.
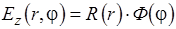
помножим уравнение 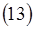 на
на 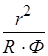 и заменим
и заменим 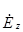 на
на 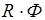 :
:
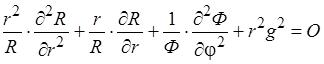
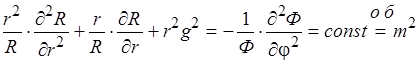
В данном уравнении левая часть зависит от 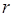 , а правая от
, а правая от 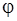 . Переходим к двум уравнениям от одной переменной:
. Переходим к двум уравнениям от одной переменной:
1) 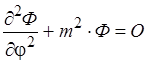 . Общее решение данного уравнения:
. Общее решение данного уравнения:
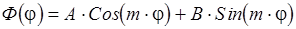
т. к. 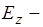 чётная функция, то
чётная функция, то 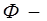 тоже чётная функция, а
тоже чётная функция, а 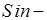 нечётная функция, следовательно
нечётная функция, следовательно 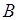 должно быть
должно быть 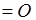 . Отсюда получаем :
. Отсюда получаем :
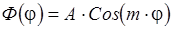
Решение будет однозначным, если 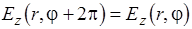 .
.
Отсюда :
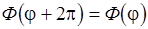
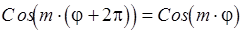 , где
, где

2) 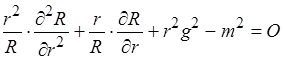
Помножим данное уравнение на 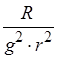 (
( 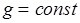 и мы можем внести её под знак дифференциала.)
и мы можем внести её под знак дифференциала.)
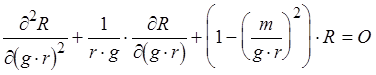
Общим решением этого уравнения будет:
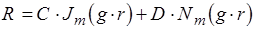 , где
, где
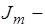 функция Бесселя первого рода
функция Бесселя первого рода 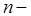 ого порядка
ого порядка
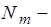 функция Бесселя второго рода
функция Бесселя второго рода 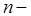 ого порядка
ого порядка
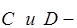 постоянные интегрирования.
постоянные интегрирования.
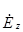 при
при  и любом
и любом 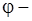 величина конечная, следовательно, т. к.
величина конечная, следовательно, т. к. 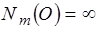 то
то 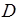 должно быть
должно быть 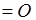 , чтобы
, чтобы 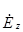 было конечным. Отсюда:
было конечным. Отсюда:
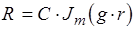
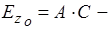 обусловлено мощностью электрической волны в начале линии. Тогда:
обусловлено мощностью электрической волны в начале линии. Тогда:
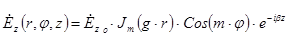
Мы нашли только одну составляющую. Для того чтоб найти остальные составляющие воспользуемся уравнениями Максвелла 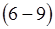 . В итоге получим:
. В итоге получим:
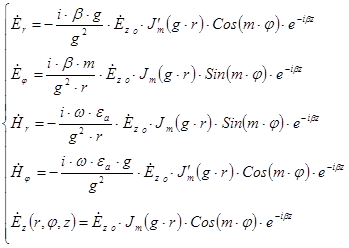
где 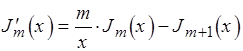
C помощью данной системы можно описать поле волны для 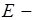 волн в круглом волноводе.
волн в круглом волноводе.
Исследуем 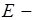 волны. Граничное условие
волны. Граничное условие 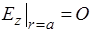 . Отсюда следует, что
. Отсюда следует, что 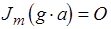
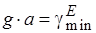
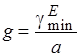
Приведём примеры критических частот некоторых видов волн :
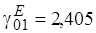
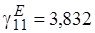
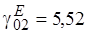
Отсюда видно, что минимальной критической среди 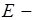 волн частотой обладает волна
волн частотой обладает волна 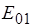 .
.
4.2.6. Магнитные волны ( 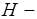 волны)
волны)
Волновое уравнение для продольной составляющей 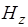 записывается в цилиндрической системе координат следующим образом:
записывается в цилиндрической системе координат следующим образом:
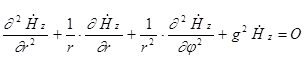
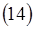
сравним уравнение 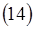 с уравнением
с уравнением 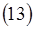 из предыдущей темы. Легко заметить, что уравнения аналогичны. Поэтому общее решение этого уравнения будет тоже аналогично :
из предыдущей темы. Легко заметить, что уравнения аналогичны. Поэтому общее решение этого уравнения будет тоже аналогично :
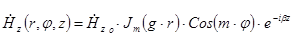
Мы нашли только одну составляющую. Для того чтоб найти остальные составляющие воспользуемся уравнениями Максвелла 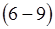 . В итоге получим:
. В итоге получим:
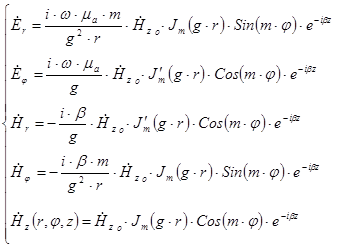
где 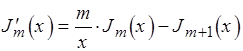
C помощью данной системы можно описать поле волны для 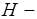 волн в круглом волноводе.
волн в круглом волноводе.
Исследуем 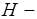 волны. Граничное условие
волны. Граничное условие 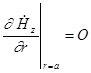 . Отсюда:
. Отсюда:
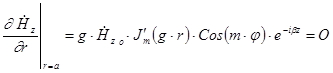
 |
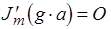
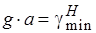
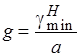
Приведём примеры критических частот некоторых видов волн:
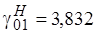
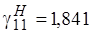
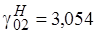
Отсюда видно, что минимальной критической среди 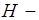 волн частотой обладает волна
волн частотой обладает волна 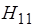 . Эта же волна является минимальной критической и среди
. Эта же волна является минимальной критической и среди 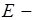 волн. Это значит, что при одной и той же частоте можно использовать конструкцию меньшего диаметра.
волн. Это значит, что при одной и той же частоте можно использовать конструкцию меньшего диаметра.
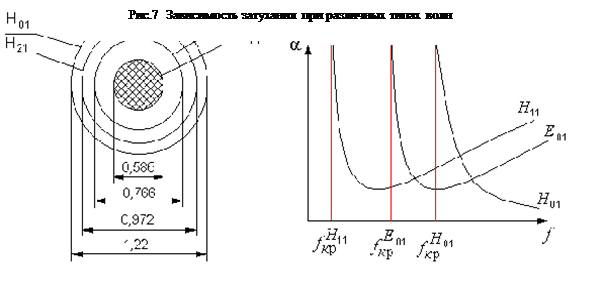
Нарисуем диаграмму критических размеров волновода для разных типов волн:
Из диаграммы на рис.7 следует, что для передачи лучше всего выбрать 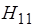 , но на практике используют волну
, но на практике используют волну 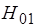 т. к. при росте частоты у этой волны наблюдается уменьшение коэффициента затухания (см. рис. 7).
т. к. при росте частоты у этой волны наблюдается уменьшение коэффициента затухания (см. рис. 7).
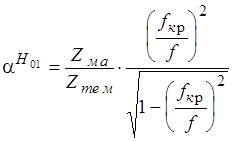
где 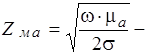 активная составляющая волны в металле.
активная составляющая волны в металле.
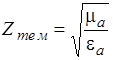
У 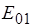 и
и 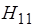 затухание растёт с ростом частоты благодаря возникновению поверхностного эффекта, что означает уменьшение эффективного поперечного сечения волновода.
затухание растёт с ростом частоты благодаря возникновению поверхностного эффекта, что означает уменьшение эффективного поперечного сечения волновода.
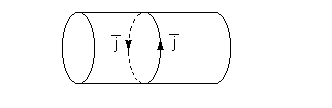
Теперь исследуем волну 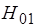 . Для этой волны линии напряжённости электрического поля идут так:
. Для этой волны линии напряжённости электрического поля идут так:

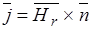
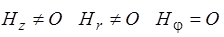
Из рисунка видно, что вектор плотности тока 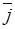 направлен по окружности.
направлен по окружности.
Из рисунка видно, что 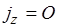
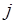 ~
~ 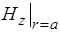 . С ростом частоты происходит уменьшение составляющей электромагнитного поля
. С ростом частоты происходит уменьшение составляющей электромагнитного поля 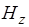 , что приводит к уменьшению плотности тока и следовательно с ростом частоты происходит снижение коэффициента затухания
, что приводит к уменьшению плотности тока и следовательно с ростом частоты происходит снижение коэффициента затухания 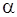 . Для примера можно привести соотношение коэффициентов затухания на частоте 15 Ггц:
. Для примера можно привести соотношение коэффициентов затухания на частоте 15 Ггц:
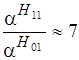 .
.
К недостаткам волновода при передаче данного типа волны можно отнести то, что при отрыве волны от стенок волновода происходит искажение картины поля, что ведёт к резкому увеличению затухания. Борются с этим путём изготовления волноводов с высокой однородностью, а так же путём использования спиральных волноводов, которые выполняются из изолированного медного проводника круглого или прямоугольного сечения. Такие волноводы могут пропускать только волну 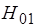 . Для остальных типов волн этот волновод является фильтром.
. Для остальных типов волн этот волновод является фильтром.
4.2.7. Классификация и структура волн в волноводах
В волноводах могут распространяться лишь волны высшего порядка: электрические (Еmn) и магнитные (Hmn)
 |
На рисунке показана структура волн Н11 и Е01 в цилиндрическом волноводе. Можно отметить, что:
1) линии электрического и магнитного полей внутри волноводов расположены взаимно – перпендикулярно.
2) электрические линии в большинстве случаев замыкаются на стенках волновода и имеют перпендикулярное направление у стенок.
3) магнитные линии имеют замкнутые пути вокруг электрических линий и не касаются стенок волновода.
 Наибольший интерес для связи, представляет распространение на большие расстояния поперечно–электрической волны Е01 (или Н01), в цилиндрических волноводах.
Наибольший интерес для связи, представляет распространение на большие расстояния поперечно–электрической волны Е01 (или Н01), в цилиндрических волноводах.
 Как видно из графиков, затухание этой волны, в отличие от других волн, с увеличением частоты уменьшается, причем, чем короче волна, тем меньше потери и соответственно затухание энергии в волноводе. Падающая частотная характеристика является специфической особенностью волны Н01 лишь в цилиндрическом волноводе, и не может быть воспроизведена ни в каком другом типе линий передач. Это обусловлено особой конфигурацией поля волны Н01, электрические силовые линии которого циркулируют по поперечным замкнутым путям и не соприкасаются со стенками волновода. В результате отсутствует свойственный волнам других типов ток проводимости в стенках волновода и потери в них.
Как видно из графиков, затухание этой волны, в отличие от других волн, с увеличением частоты уменьшается, причем, чем короче волна, тем меньше потери и соответственно затухание энергии в волноводе. Падающая частотная характеристика является специфической особенностью волны Н01 лишь в цилиндрическом волноводе, и не может быть воспроизведена ни в каком другом типе линий передач. Это обусловлено особой конфигурацией поля волны Н01, электрические силовые линии которого циркулируют по поперечным замкнутым путям и не соприкасаются со стенками волновода. В результате отсутствует свойственный волнам других типов ток проводимости в стенках волновода и потери в них.
 |
 С ростом частоты круговое поле Н01 все больше отрывается от стенок волновода, и потери уменьшаются.
С ростом частоты круговое поле Н01 все больше отрывается от стенок волновода, и потери уменьшаются.
Так же это можно объяснить иначе – исходя из теории зигзагообразного распространения волн в волноводах. С ростом частоты уменьшается число отражений от стенок волновода, уменьшается общая длина зигзагообразной линии, и соответственно уменьшаются потери передачи.
Из рис. следует, что волна Н10 находится в существенно привилегированном положении по сравнению с волнами других типов: затухание волны Н01 на частоте 15 ГГц в 7 раз меньше затухания волны Н11. Однако волне Н01 свойственны некоторые недостатки. Это обусловлено природой и конфигурацией электромагнитного поля Н01. Линии электрических и магнитных полей волны Н01 не имеют связи с самим волноводом, и поэтому она сравнительно неустойчива и весьма чувствительна к магнитным деформациям и неоднородностям волновода. Борьба с этим недостатком волны идет по трем направлениям:
1) стремление к максимальной однородности волноводного трактата передачи
2) применение спирального волновода периодической структуры, обладающие фильтрующими свойствами пропускать волну Н01 и задерживать все остальные типы волн.
Электрический расчет цилиндрических волноводов
Коэффициент фазы [раз/км]: 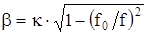
Где 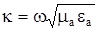 – волновое число среды
– волновое число среды
Фазовая скорость, [км/с]: 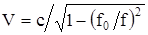
Волновое сопротивление, [Ом]:
Для Е–волн 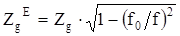
Для Н–волн 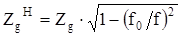
Где 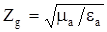 – волновое сопротивление д/э основной волны.
– волновое сопротивление д/э основной волны.
(Для воздуха Zo=376,8 Ом)
Коэффициент затухания, [дБ/км]:
Для Е–волн 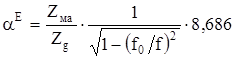
Для Н–волн 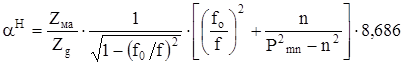
Где n – порядок бесселевой функции.
Для волны Н01, у которой n = 0, коэффициент затухания определится формулой:
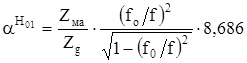
Где 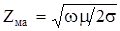 – волновое сопротивление металла (активная часть)
– волновое сопротивление металла (активная часть)
В замкнутых металлических волноводах стенки полностью экранируют передаваемую волну и направляют ее вдоль волновода. В волноводах со спиральной токонесущей поверхностью имеются периодически повторяющие по длине разрывы цепи, являющиеся причиной излучения энергии. Поэтому в спиральных волноводах лишь часть энергии передается внутри волновода, а часть излучается в окружающее пространство, излучение зависит от шага наложения спирали, ширины щелей и выражается через коэффициент: 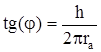 ;
;
где h – шаг спирали;
rа – внутренний радиус волновода;
Чем реже намотана спираль, тем больше ширина щелей и естественно, больше сказывается эффект излучения энергии в окружающее пространство.
Излучение энергии сопровождается дополнительными потерями на излучение. Поэтому в спиральных волноводах общие потери могут быть оценены как сумма потерь в металлической стенке волновода aм и потерь на щелевое излучение aи:
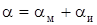
В сплошных металлических волноводах имеются потери лишь в металле aм. Коэффициент затухания за счет потерь на излучение в спиральных волноводах определяется из уравнения:
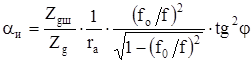
Где 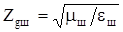 – волновое сопротивление шланга
– волновое сопротивление шланга
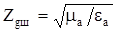 – волновое сопротивление диэлектрика внутри волновода
– волновое сопротивление диэлектрика внутри волновода
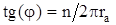 – параметр спиральности
– параметр спиральности
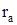 – внутренний радиус волновода
– внутренний радиус волновода
Из этого уравнения следует, что потери существенно возрастают с увеличением шага спирали h. Так, при изменении h от 1 до 2 мм затухание возрастает от 3,5 до 17 дБ/м.
Дата добавления: 2017-01-16; просмотров: 4724;











