Дифференциальные уравнения в области профессиональной деятельности.

Задача 1. (охлаждение тела).

Скорость охлаждения тела в воздухе пропорциональна разности между температурой тела и температурой воздуха. Температура воздуха 20 ⁰ С. Известно, что в течение 20 минут тело охлаждается от 100 ⁰ С до 60 ⁰ С. Определить закон изменения температуры 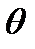тела в зависимости от времени t.

Решение:

Согласно условия задачи имеем 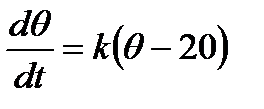, где k – коэффициент пропорциональности.

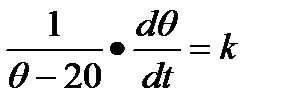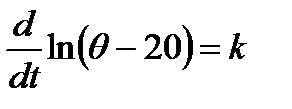Отсюда или и , значит 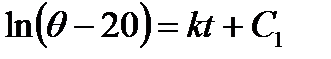, что дает 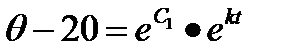и, следовательно .

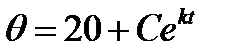Для определения С используем начальное условие: при t = 0, 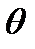= 100.

Отсюда С = 100 - 20 = 80

Поэтому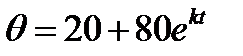

Коэффициент пропорциональности k определяет из дополнительного условия при t = 2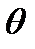0, = 60.

Отсюда 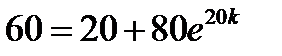или 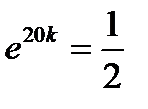и, следовательно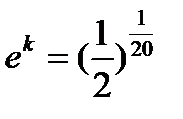

Итак, искомая функция .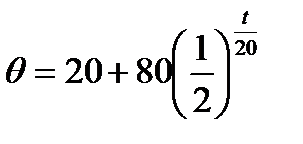

Теория эпидемий.

Ограничимся рассмотрением эпидемии простейшего вида. Предположим, что изучаемое заболевание носит длительный характер, так что процесс передачи инфекции значительно более быстрый, чем течение самой болезни. Нас будет интересовать именно первый процесс – процесс передачи инфекции. При этом будет предполагать, что заражение особи не удаляются из колонии и передают при встречах инфекцию незараженных.

Пусть а и n – соответственно число зараженных и незараженных в начальный момент, х=х(t) – число незараженных в момент времени t, а у=у(t) – число зараженных к моменту t. Для всех моментов времени из некоторого не слишком большого отрезка 0 ≤ t ≤ T (отрезок [0;Т] должен быть меньше времени жизни одного поколения, тогда в наших уравнениях мы можем не учитывать естественную смертность особей) имеет место равенство х+у=n+a

Так как инфекция передается при встречах зараженных с незараженными, то число незараженных будет учитывать с течением времени пропорционально количеству встреч между теми и другими, т.е. пропорционально ху. Поэтому скорость убывания числа незараженных равна 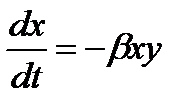, где β – коэффициент пропорциональности. Подставим в равенство 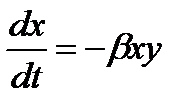выражение у из х+у=n+a, получим .

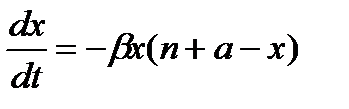Отсюда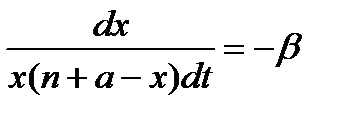

Или

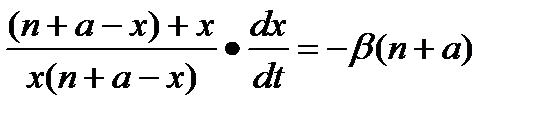откуда

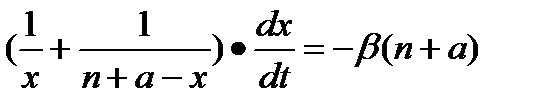
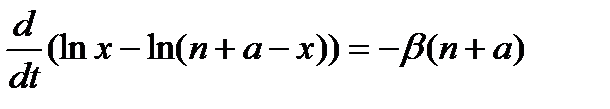и, значит,

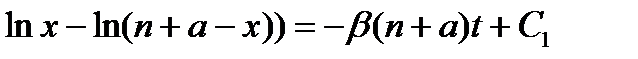или

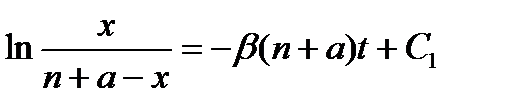, что дает

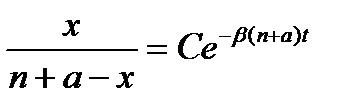
Для определения С используем начальное условие: при t= 0 число незараженных равно n, т.е. при t = 0, х = n.

Имеем С = 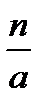и, значит,

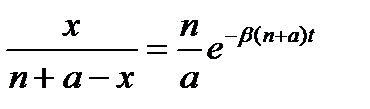
Разрешая последнее уравнение относительно х, получим окончательно

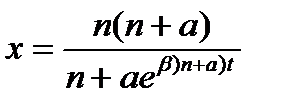
Эта формула дает закон убывания х с течением времени.