Приложения определенного интеграла.
Если известна скорость прямолинейного движения материальной точки
ν = ν(t), то можно найти путь, пройденный этой точкой за промежуток времени от t0 до Т. В самом деле, из определения ν(t) следует, что эта функция является производной от закона движения точки S = S(t) в момент t и, следовательно, S(t) есть первообразная для ν(t). Поэтому по формуле Ньютона-Лейбница S(T) – S(t0) = 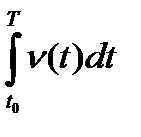
Пример: Рассмотрим популяцию бактерий, в которой масса особи меняется в течение жизни, и подсчитаем общую биомассу популяции.
Пусть β означает возраст в тех или иных единицах времени, а р(β) – число особей популяции, возраст которых равен β. Пусть, наконец, μ(β) – средняя масса особи возраста β, а М(β) – биомасса всех особей в возрасте от 0 до β.
Заметив, что произведение р(β) μ(β) равно биомассе всех особей возраста β, рассмотрим разность М (β + Δ β) – М(β), где Δ β>0.Очевидно, что эта разность, равная биомассе всх особей в возрасте от β до β + Δ β, удовлетворяет неравенствам:
р( 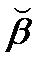 ) μ(
) μ( 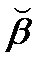 ) Δ β ≤ М (β + Δ β) – М(β) ≤ р(
) Δ β ≤ М (β + Δ β) – М(β) ≤ р( 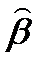 ) μ(
) μ( 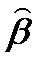 ) Δ β,
) Δ β,
где р( 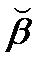 ) μ(
) μ( 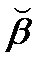 ) - наименьшее, а р(
) - наименьшее, а р( 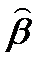 ) μ(
) μ( 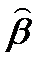 )– наибольшее значения функции, р(β) μ(β) на отрезке [β ; β + Δ β]. Учитывая , что Δ β>0, из нашего неравенства имеем: р(
)– наибольшее значения функции, р(β) μ(β) на отрезке [β ; β + Δ β]. Учитывая , что Δ β>0, из нашего неравенства имеем: р( 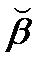 ) μ(
) μ( 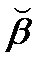 ) ≤ (М (β + Δ β) – М(β)) / Δ β ≤ р(
) ≤ (М (β + Δ β) – М(β)) / Δ β ≤ р( 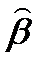 ) μ(
) μ( 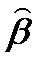 ).
).
Из непрерывности функции р(β) μ(β) следует, что
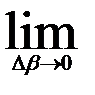 р(
р( 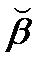 ) μ(
) μ( 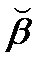 ) =
) = 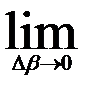 р(
р( 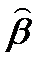 ) μ(
) μ( 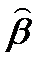 ) = р(β) μ(β).
) = р(β) μ(β).
Поэтому будем иметь 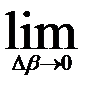 (М (β + Δ β) – М(β)) / Δ β = р(β) μ(β).
(М (β + Δ β) – М(β)) / Δ β = р(β) μ(β).
Или производная от (М (β + Δ β) – М(β)) / Δ β равна р(β) μ(β).
Следовательно, биомасса М(β) является первообразной для функции р(β) μ(β).
Отсюда: М(Т) – М(0) = 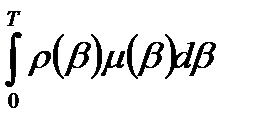
Где Т – максимальный возраст особи в данной популяции.
Так как М(0), очевидно, равно нулю, то окончательно получаем
М(Т) = 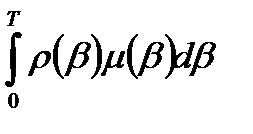 .
.

Дата добавления: 2016-06-05; просмотров: 2558;











