Задачи на экстремум функции.

Напомним следующее правило исследования функции f(x) на экстремум.

Чтобы найти точки экстремума данной функции f(x), следует:

1) Найти первую производную функция у = f(x) и, приравняв ее к нулю, вычислить действительные корни полученного уравнения f^/(x) = 0.

2) Найти вторую производную f^//(x).

3) Вычислить значение второй производной для каждого значения х, являющегося корнем первой производной.

Если при этом окажется, что f^//(x)≠0, где х₀ – взятый корень, то при х = х₀ функция f(x) имеет экстремум:

Максимум, если f^//(x)<0, и минимум, если f^//(x)>0.

Рассмотрим следующие задачи:

Задача №1: В питательную среду вносят популяцию из 1000 бактерий. Численность популяции возрастает по закону р(t) = 1000 + 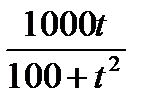, где t

Выражается в часах. Найти максимальный размер этой популяции.

Решение. Имеем:

р^/(t) =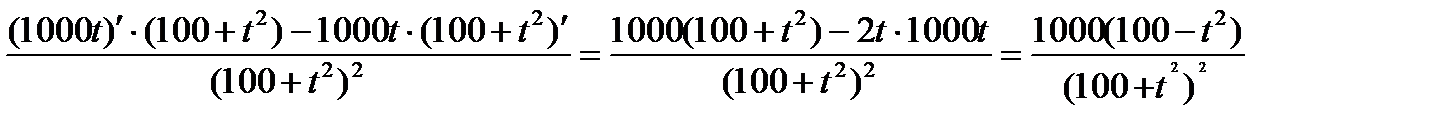

р^//(t) = (р^/(t))^/ =-2000t· 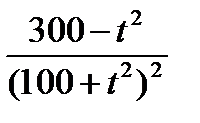(предлагаем вам самостоятельно найти данную производную и сравнить полученный результат).

Так как р^/(10) = 0 и р^// (10) <0, то максимальный размер популяции составляет р(10) = 1050 и достигается по происшествии 10 часов роста.

Задача №2.Реакция организма на введенное лекарство может выражаться повышением кровяного давления, уменьшением температуры тела, изменением пульса или других физиологических показателей. Степень реакции зависит от назначенной дозы лекарства. Предположим, что х обозначает дозу назначенного лекарства, а степень реакции у описывается функцией у = R(x) = x²(a – x), где а – некоторое положительное постоянное. При каком значении х реакция максимальна?

Решение. Имеем f^/ (x) = (x²(a – x))^/ = (х²)^/· (a – x) + x²(a – x)^\ =2х(a – x) – х² =

= 2ax – 3x², f^// (x) = (2a – 6x.

Так как х = 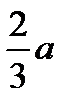- корень уравнения f^/ (x) = 0 и f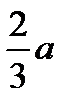^// ( ) = -2а <0, то х = 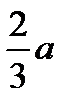- тот уровень дозы, который дает максимальную реакцию.

Задача №3.

Газовая смесь, необходимая для лабораторных исследований, состоит из окиси азота (NO) и кислорода (О₂). Требуется найти концентрацию О₂, при которой содержащаяся в смеси окись азота окисляется с наибольшей скоростью

Решение.

В условиях практической необходимости скорость ν реакции 2NO + O₂ = 2NO₂ выражается формулой ν = kx²y, где х – концентрация NO в любой момент времени, у – концентрация О₂, k – константа скорости реакции, зависящая только от температуры и не зависящая от концентрации реагирующих компонентов. Концентрацию газов будем выражать в объёмных процентах. В этом случае у = 100 – х и ν = kx²(100 –х). очевидно, 0<x<100. Производная ν^/(х) = (kx²(100 –х))^/ = 2kx(100 – x) - kx² = k(200x – 3x²) между 0 и 100 имеет один единственный корень х = х₁ = 200/3≈66,67. Вторая производная равна

ν^//(х) = (k(200x – 3x²))^/ = k(200 – 6x) и ν^//(х₁)<0 . Значит в точке х₁ – максимум функции. Следовательно, скорость реакции наибольшая, когда х = 66,67% и у = 33,33%