Основное уравнение влияния между однородными

кабельными цепями

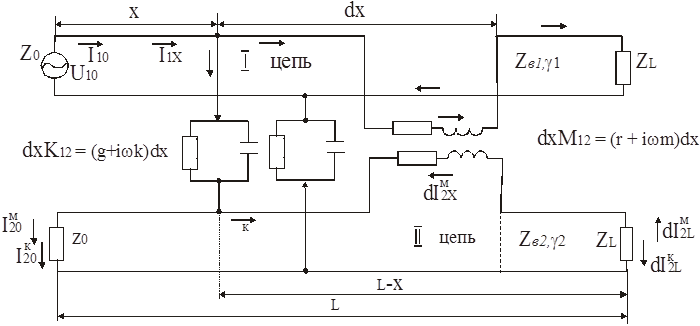
Рассмотрим мешающее влияние между двумя параллельно расположенными цепями за счет наличия между ними электромагнитной связи. Нагрузочные сопротивления в начале и конце цепи согласованны (Zo = Z_L = Zв)

Ток в любой точке цепи I на расстоянии x от начала 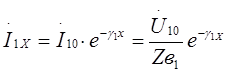, (21)

а напряжение

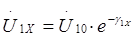, (22)

где Zв₁ и g₁ – волновое сопротивление и коэффициент распространения первой цепи.

Определим отдельно влияния за счет магнитного и электрического полей на элементарном участке dx. Э.д.с. во второй цепи за счет магнитного поля

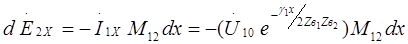(23)

Под воздействием э.д.с. возникает ток

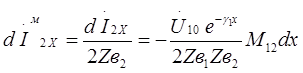(24)

За счет электрического влияния во второй цепи ток на участке dx

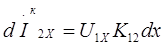(25)

Этот ток разветвляется на две равные части. Ток, направляющийся к ближнему концу

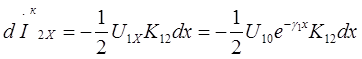(26)

Ток, направляющийся к дальнему концу

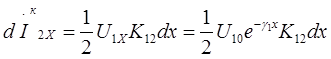(27)

Суммарный ток влияния на ближнем конце цепи, подверженной влиянию, наводимый электромагнитным полем влияющей цепи на участке dx

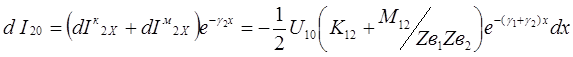(28)

Аналогично для суммарного тока влияния на дальнем конце линии от влияния на элементе dx получим

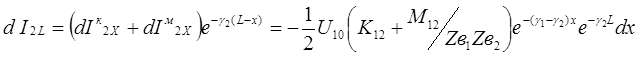(29)

Для определения полного тока влияния на концах линии(?*), длиной L , проинтегрируем оба выражения в пределах от 0 до L.

На ближнем конце

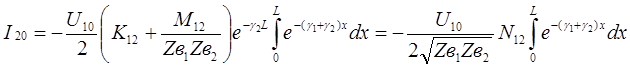
(30)

На дальнем конце

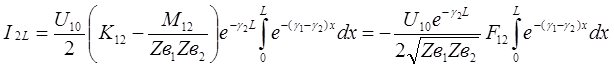
(31)

где :

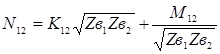- электромагнитная связь на ближнем конце

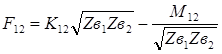- электромагнитная связь на дальнем конце

Имея ввиду, что 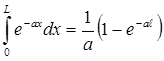, получим:

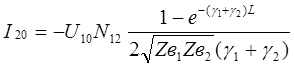, и (32)

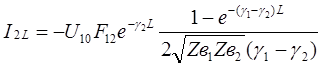(33)

С учетом того, что переходное затухание между цепями на ближнем и дальнем концах определяется:

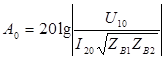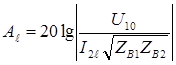и (34)

получим

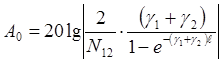и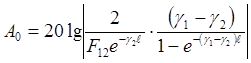

(35)

Указанные уравнения справедливы для расчета переходного затухания между продольными (коаксиальными) нескрученными цепями, в которых известен коэффициент фазы цепи и закон его изменения вдоль линии.

Кабельные линии состоят из строительных длин со скрученными цепями: здесь не известна фаза сложения влияний с отдельных длин кабеля. Поэтому при расчете влияния и переходного затухания в кабельных линиях принимается геометрический закон сложения влияния с отдельных строительных длин кабеля.

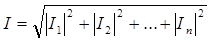(36)

На этом основании для кабельных линий полный ток влияния на ближнем и дальнем концах запишется

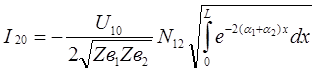; (37) 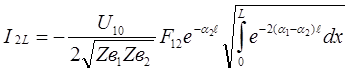; (38)

После интегрирования получим :

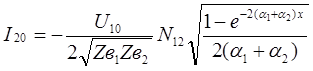; (39) 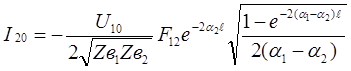(40)

Переходные затухания , дБ, на ближнем и дальнем концах равны :

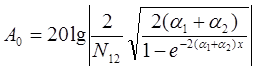и (41) 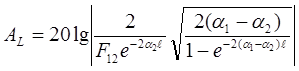(42)

В кабельных цепях a₁ = a₂ = a и Zв₁ = Zв₂ = Zв, поэтому можно записать

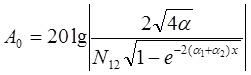и (43)

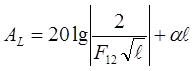(44)

Соответственно защищенность, дБ

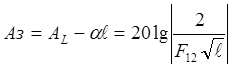(45)

При выводе формулы для А_L имелось ввиду, что

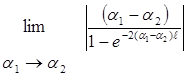(46)

Для кабельных линий Ао, А_L, Аз через строительные длины выражения примут вид :

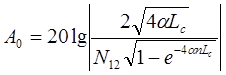; (47)

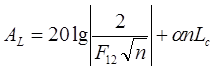; (48)

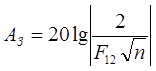(49)

где:

L_c – строительная длина кабеля, км;

n – число строительных длин;

N₁₂ и F₁₂ – электромагнитные связи строительной длины кабеля.

N₁₂ = K₁₂Z_в + M₁₂ / Z_в ; F₁₂ = K₁₂Z_в - M₁₂ / Z_в ;