Волновая функция и ее физический смысл.
Какой физический смысл следует придать введенной нами волновой функции?
Мы уже обсуждали это вопрос и пришли к выводу, что это поле 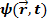 определяет вероятность обнаружить частицу в различных точках пространства в заданный момент времени. Точнее, квадрат модуля волновой функции
определяет вероятность обнаружить частицу в различных точках пространства в заданный момент времени. Точнее, квадрат модуля волновой функции 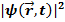 есть плотность вероятности обнаружить частицу в точке с координатой
есть плотность вероятности обнаружить частицу в точке с координатой 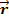 в момент времени t :
в момент времени t :
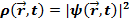 (17.15)
(17.15)
Естественно полагать, что где-то в пространстве частица достоверно существует. По-
этому волновая функция должна удовлетворять следующему условию нормировки
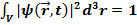 (17.16)
(17.16)
Здесь интеграл берется по области определения волновой функции, как правило, это все бесконечное пространство. Таким образом, состояния частицы должны описываться функциями с интегрируемым квадратом модуля.
Здесь нас ожидает «неприятность». Единственная волновая функция, которую мы уже знаем, это волна де Бройля, соответствующая частице с заданным значением импульса. Поскольку для этой волны
ng w:val="EN-US"/></w:rPr><m:t>1</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 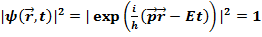 (17.17)
(17.17)
то нормировочный интеграл, очевидно, расходится. С другой стороны, такая ситуация
понятна. Если импульс известен точно (а для волны де Бройля это именно так), то из соотношения неопределенностей для неопределенности координаты получаем
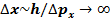 (17.18)
(17.18)
т.е. частица делокализована по всему бесконечному пространству. Именно такое абсолютно делокализованное состояние и задает плоская волна. Конечно, к реальному состоянию частицы плоская волна прямого отношения не имеет. Это математическая абстракция. Любой физический процесс происходит, может быть и в макроскопически большой, но ограниченной области пространства. Поэтому мы можем утверждать, что состояние частицы с точно определенным значением импульса принципиально невозможно, а волновая функция вида (17.1) или (17.7) не описывает никакого состояния реаль ного физического объекта. С другой стороны, если волновой пакет достаточно широкий, т.е. его пространственной размер много больше длин волн де Бройля его образующих, приближение плоской волны часто оказывается очень удобным с математической точки зрения.
Таким образом, помимо функций с интегрируемым квадратом модуля в квантовой механике бывает удобно работать и с функциями, которые условию нормировки
(6.16) не удовлетворяют. Рассмотрим вопрос о нормировке таких функций на примере состояния (6.1). Мы опять для простоты ограничимся одномерным случаем. Будем считать, что состояние в виде плоской волны
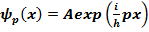 (17.19)
(17.19)
(A = 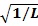 - нормировочная константа, индекс « p » указывает, что это состояние с импульсом p ) задано на отрезке x∈(− L/2, L/2). Мы полагаем, что L велико и в дальнейшем перейдем к пределу L →∞.
- нормировочная константа, индекс « p » указывает, что это состояние с импульсом p ) задано на отрезке x∈(− L/2, L/2). Мы полагаем, что L велико и в дальнейшем перейдем к пределу L →∞.
Рассмотрим значение следующего интеграла
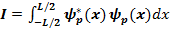 (17.20)
(17.20)
Вычисление интеграла (17.20) дает
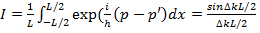 (17.21)
(17.21)
Здесь Δk = (p − p') h . При Δk ≠ 0 в пределе L →∞ получаем, что I →0 , т.е. волновые функции состояний с различными значениями импульса становятся ортогональны друг другу. В случае Δk ≡ 0 получаем, что I = 1 для любого конечного сколь угодно большого значения L , т.е. условие нормировки (17.16) оказывается выполненным. Указанная процедура может быть использована при решении конкретных задач, однако не совсем удобна, так как в исходной функции (17.19) появился нормировочный размер L . Поэтому обычно поступают немного иначе. Пусть нормировочная константа A = 1. Тогда вычисление интеграла (17.21) в пределе L →∞ дает
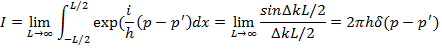
Мы здесь использовали известные соотношения 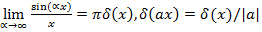
Отсюда возникает условие нормировки на δ - функцию:
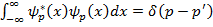 (17.22)
(17.22)
где 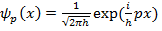 (17.23)
(17.23)
В трехмерном случае аналогично получаем 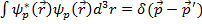 (17.24)
(17.24)
причем 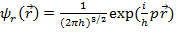 (17.25)
(17.25)
Условие нормировки на δ - функцию используется в квантовой теории всякий раз, когда
волновая функция не может быть нормирована согласно условию (17.16).
Опыт Франка-Герца
Опыт Франка — Герца — опыт, явившийся экспериментальным доказательством дискретности внутренней энергии атома. Поставлен в 1913 Дж. Франком и Г. Герцем.
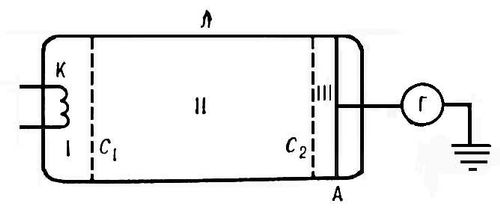
Рис. 17. 1
На рисунке приведена схема опыта. К катоду К и сетке C1 электровакуумной трубки, наполненной парами Hg (ртути), прикладывается разность потенциалов V, ускоряющая электроны, и снимается вольт-амперная характеристика. К сетке C2 и аноду А прикладывается замедляющая разность потенциалов. Ускоренные в области I электроны испытывают соударения с атомами Hg в области II. Если энергия электронов после соударения достаточна для преодоления замедляющего потенциала в области III, то они попадут на анод. Следовательно, показания гальванометра Г зависят от потери электронами энергии при ударе.
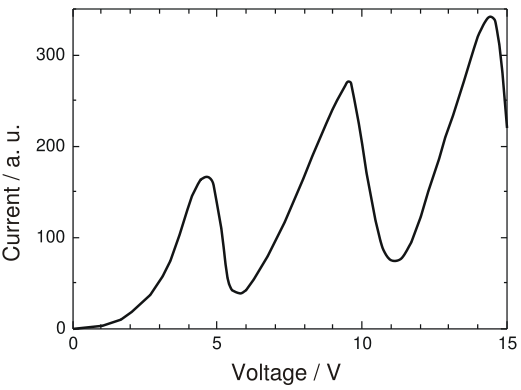
Рис. 17. 2
В опыте наблюдался монотонный рост тока I при увеличении ускоряющего напряжения вплоть до 4,9 В, то есть электроны с энергией Е < 4,9 эВ испытывали упругие соударения с атомами Hg, и внутренняя энергия атомов не менялась. При значении V = 4,9 В (и кратных ему значениях 9,8 В, 14,7 В) появлялись резкие спады тока. Это определённым образом указывало на то, что при этих значениях V соударения электронов с атомами носят неупругий характер, то есть энергия электронов достаточна для возбуждения атомов Hg. При кратных 4,9 эВ значениях энергии электроны могут испытывать неупругие столкновения несколько раз.
Таким образом, опыт Франка — Герца показал, что спектр поглощаемой атомом энергии не непрерывен, а дискретен, минимальная порция (квант электромагнитного поля), которую может поглотить атом Hg, равна 4,9 эВ. Значение длины волны λ = 253,7 нм свечения паров Hg, возникавшее при V > 4,9 В, оказалось в соответствии со вторым постулатом Бора
Принцип Паули.
На первый взгляд представляется, что в атоме все электроны должны заполнить уровень с наименьшей возможной энергией. Опыт же показывает, что это не так.
Действительно, в соответствии с принципом Паули, в атоме не может быть электронов с одинаковыми значениями всех четырёх квантовых чисел.
Каждому значению главного квантового числа п соответствует 2п2 состояний, отличающихся друг от друга значениями квантовых чисел l, m и mS.
Совокупность электронов атома с одинаковыми значения квантового числа п образует так называемую оболочку. В соответствии с номером п
| Значение п | 1 | 2 | 3 | 4 | 5 |
| Оболочка | К | L | M | N | O |
| Число возможных состояний | 2 | 8 | 18 | 32 | 50 |
Таблица 18. 1
Оболочки подразделяются на подоболочки , отличающиеся квантовым числом l . Число состояний в подоболочке равно 2(2l + 1).
Различные состояния в подоболочке отличаются значениями квантовых чисел т и mS . 
| Оболочка | K | L | M | ||||||||||||
| Значение n | |||||||||||||||
| Подоболочка (n,l) | 1s | 2s | 2p | 3s | 3p | 3d | |||||||||
| ml ms | ↑↓ | ↑↓ | +1 ↑↓ | ↑↓ | -1 ↑↓ | ↑↓ | +1 ↑↓ | ↑↓ | -1 ↑↓ | +2 ↑↓ | +1 ↑↓ | ↑↓ | -1 ↑↓ | -2 ↑↓ | |
| Число электронов в подоболочке | |||||||||||||||
| Число электронов в оболочке | |||||||||||||||
Таблица 18. 2
Понимание периодической системы элементов основано на идее об оболочечной структуре электронного облака атома.
Каждый следующий атом получается из предыдущего добавлением заряда ядра на единицу (е) и добавлением одного электрона, который помещают в разрешённое принципом Паули состояние с наименьшей энергией.
Дата добавления: 2017-01-16; просмотров: 2270;











