Релятивистское волновое уравнение.

Прежде чем перейти к обсуждению важнейшего вопроса теории о физическом смысле волновой функции и о том, как по известной волновой функции определять измеряемые в экспериментах параметры микрообъекта, попытаемся получить («угадать») релятивистское волновое уравнение. Как известно, в релятивистской теории пространственные координаты и время образуют единый четырехмерный вектор. Поэтому в релятивистское волновое уравнение производные по времени и по пространственным координатам должны входить симметричным образом: например, уравнение может содержать производные второго (или первого) порядка и по времени и по координате.

Для релятивистской частицы связь энергии и импульса задается соотношением

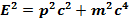(17.12)

Поэтому дисперсионное соотношение ω(k) для волны де Бройля записывается в виде

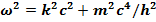(17.13)

Теперь легко угадывается волновое уравнение, допускающее решение в виде плоской

волны (17.1) с зависимостью ω(k) в виде (17.13):

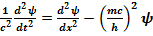(17.14)

Полученное уравнение называется уравнением Клейна – Гордона и было получено ими

в 1926 году. В частном случае, если масса частицы равна нулю (фотон), уравнение (17.14)

превращается в «обычное» волновое уравнение, описывающее, например, электромагнитное поле. Мы не будем здесь обсуждать целый комплекс проблем, возникших с толкованием смысла уравнения Клейна – Гордона в квантовой теории. Отметим только, что оказывается возможным написать еще одно релятивистское волновое уравнение, содержащее только производные первого порядка по времени и по пространственной координате, такое, что его решением является плоская волна де Бройля (17.1), а связь ω(k) задается с помощью (17.13). Соответствующее уравнение было получено Дираком в 1928 году и носит его имя.