Параметрические критерии.

Метод Стьюдента используют для сравнительной оценки средних величин. Он позволяет судить на основании экспериментальных данных о равенстве или неравенстве двух средних нормальных совокупностей и используется при условии, что:

1.Изучаемые совокупности распределены по нормальному закону.

2. Генеральные дисперсии одинаковы.

Этапы применения методов.

1.Из опытных данных следует вычислить так называемое фактическое значение критерия t_ср.

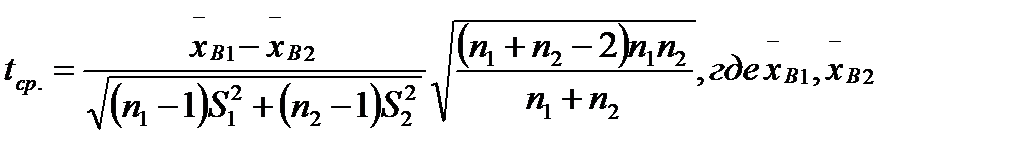- среднее выборочное для первой и второй совокупности; 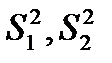- исправленные выборочные дисперсии для первой и второй совокупности; n₁ и n₂ – число значений исследуемой в первой и второй совокупностях.

2.следует найти табличное значение критерия t_st. Эта величина зависит от значения параметров k = n₁ + n₂ -2 и а– уровень значимости.

3. следует сравнить абсолютное значение t_ф с t_st. Если 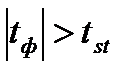нет оснований утверждать, что генеральные средние различны, если 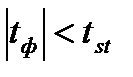, различие между генеральными средними существенно.

В медицине часто приходится подвергать анализу явления, распределения которых отличаются от нормального (оценить вкусовые качества пищевых продуктов, лекарственных препаратов). В таких случаях используют непараметрические критерии.

Критерии знаков.

При использовании этого критерия учитывается не абсолютная величина различий, а направленность сравниваемых парных наблюдений, которая обычно обозначается знаками.

Методика применения знаков:

1.определяется направленность различий сравниваемых парных наблюдений, результаты обозначаются знаками «+» и «-»; варианты, не имеющие изменений, из дальнейшей оценки исключаются;

2.подсчитывается общее число n парных наблюдений, имеющих различия(т.е. отмеченных знаками «+» и «-»);

3.подсчитывается число знаков Z_ф чаще всего встречающихся;

4.полученное число Z_ф сравнивается (с учетом n) с критическими значениями Z_st, содержащимися в таблице.

Если Z_ф≤ Z_st, то принимается нулевая гипотеза.

Если Z_ф> Z_st, то различия могут считаться значимыми с соответствующими уровнями значимости(α<0.05,α<0.01).

Критерий Ван дер Вардена обладает большей статистической мощностью, чем критерий знаков. Его применяют для проверки нулевой гипотезы при сравнении друг с другом независимых выборок.

Методика критерия:

1.сравниваемые выборки ранжируют в один общий ряд по возрастающим значениям признака.

2.каждому члену ряда присваивается порядковый номер, отмечающий его место в общем ранжированном строю.

3.по порядковым номерам одной из выборок, обычно меньше по объему, находят отношение 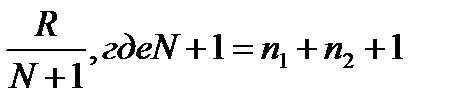, т.е сумма всех членов сравниваемых групп, увеличенная на 1; R – порядковый номер членов ряда, их «ранг».

4.с помощью специальной таблицы находят значения функции 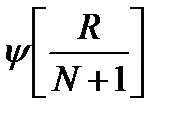, для каждого значения .

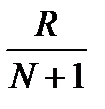5.суммируя результаты(обязательно с учетом знаков), получают величину

Х_ф =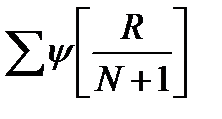

6. сравнивают Х_ф с критической точкой этого критерия Х_stдля принятого уровня значимости р и общего числа членов сравниваемых выборок N = n₁ + n₂. нулевая гипотеза сводится к предположению, что сравниваемые выборки извлечены из генеральных совокупностей с одинаковыми функциями распределения. Если окажется, что Х_ф≥Х_st, нулевая гипотеза должна быть отвергнута на принятом уровне значимости.