Конденсатор в цепи синусоидального тока

Включение конденсатора в цепь переменного тока не вызывает разрыва цепи, так как ток в цепи все время поддерживается за счет заряда и разряда кон­денсатора. Пусть напряжение (рис. 2.8 а)

.

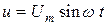Тогда

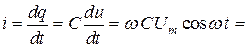
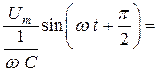
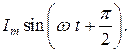(2.17)

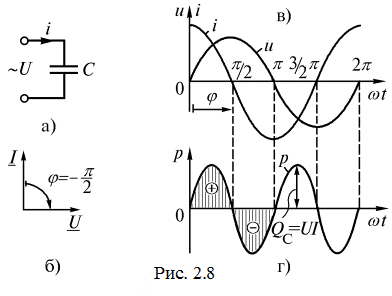Формула (2.17) показывает, что ток опережает приложенное напряжение на угол 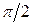(рис. 2.8 б, в). Нулевым значениям тока соответствуют максимальные значе­ния напряжения. Физически это объясняется тем, что при достижении электри­ческим зарядом и соответственно напряжением максимального значения ток стано­вится равным нулю.

Под фазовым сдвигом тока относительно напряжения здесь, как и раньше, подразумевается разность начальных фаз напряжения и тока, т.е.

.

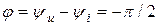Таким образом, в отличие от цепи с катушкой, где 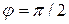, угол сдвига фаз в цепи с конденсатором отрицателен.

Из (2.17) видно, что амплитуды тока и напряжения связаны законом Ома

,

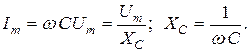где 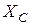– емкостное сопротивление, имеющее размерность Ом.

Мгновенная мощность, поступающая в конденсатор

,

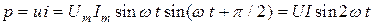колеблется синусоидально с угловой частотой 2 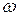, имея амплитуду, равную 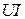(рис. 2.8 г). Поступая от источника, энергия временно запасается в электрическом поле конденсатора, затем возвращается источнику при исчезновении электриче­ского поля. Таким образом, здесь, как и в цепи с катушкой, происходит колебание энергии между источником и конденсатором, причем активная мощность 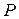= 0. Ам­плитуду колебания мощности в цепи с конденсатором называют реактивной (емко­стной) мощностью

.

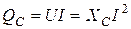2.3. Анализ цепей синусоидального тока с помощью векторных
диаграмм

Совокупность векторов, изображающих синусоидальные ЭДС, напряжения и токи одной частоты и построенных на плоскости с соблюдением их ориентации друг относительно друга, называют векторной диаграммой. Векторные диа­граммы широко применяются при анализе режимов работы цепей синусоидаль­ного тока, что делает расчет цепи наглядным.