Метод контурных токов
Расчет любой сложной электрической цепи может быть сведен к решению системы из 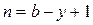 уравнений, если использовать так называемые контурные токи, т.е. токи, замыкающиеся в независимых контурах. В соответствии с этим методом составляются уравнения только по второму закону Кирхгофа, для чего выбирается необходимое число контуров. При расчете полагают, что в каждом контуре течет свой контурный ток.
уравнений, если использовать так называемые контурные токи, т.е. токи, замыкающиеся в независимых контурах. В соответствии с этим методом составляются уравнения только по второму закону Кирхгофа, для чего выбирается необходимое число контуров. При расчете полагают, что в каждом контуре течет свой контурный ток.
Последовательность расчета и вывод основных уравнений проведем применительно к схеме, показанной на рис. 1.26.
Для расчета по методу контурных токов в схеме выделяют независимые контуры. Если в левом верхнем контуре протекает ток 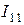 , в правом верхнем –
, в правом верхнем – 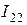 , в нижнем –
, в нижнем – 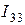 , то при направлении обхода всех контуров по часовой стрелке для контурных токов можно составить следующие уравнения по второму закону Кирхгофа
, то при направлении обхода всех контуров по часовой стрелке для контурных токов можно составить следующие уравнения по второму закону Кирхгофа
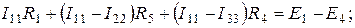
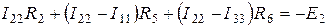 ;
;
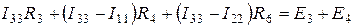 . (1.45)
. (1.45)
После преобразования получим:
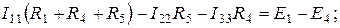
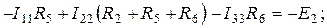
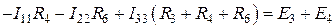 . (1.46)
. (1.46)
Введем обозначения
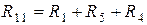 ;
; 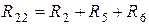 ;
; 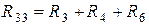 ;
;
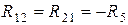 ;
; 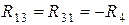 ;
; 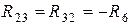 ;
;
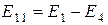 ;
; 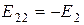 ;
; 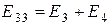 ,
,
где 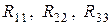 – полные или собственные сопротивления первого, второго и третьего контуров;
– полные или собственные сопротивления первого, второго и третьего контуров; 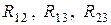 – сопротивления смежных ветвей между первым и вторым, первым и третьим, вторым и третьим контурами, взятые со знаком минус;
– сопротивления смежных ветвей между первым и вторым, первым и третьим, вторым и третьим контурами, взятые со знаком минус; 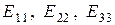 – контурные ЭДС первого, второго и третьего контуров (в нее со знаком плюс входят те ЭДС, направления которых совпадают с направлением обхода контура).
– контурные ЭДС первого, второго и третьего контуров (в нее со знаком плюс входят те ЭДС, направления которых совпадают с направлением обхода контура).
Перепишем уравнения (1.46)
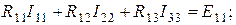
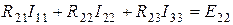 ; (1.47)
; (1.47)
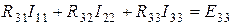 .
.
По контурным токам определяют токи в ветвях:
1) токи в наружных ветвях равны контурным токам и совпадают с ними по направлению, если контурный ток является положительным; если контурный ток – отрицательный, то направление тока в ветви меняется;
2) ток в смежной ветви, которая является общей для двух контуров, определяется как алгебраическая сумма соответствующих контурных токов.
Так, для схемы на рис. 1.26 имеем
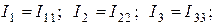
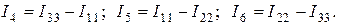
 Порядок расчета методом контурных токов:
Порядок расчета методом контурных токов:
1) для каждого независимого контура произвольно выбирают положительное направление контурного тока;
2) для каждого контура составляют уравнение (1.46) по второму закону Кирхгофа. Для этого направление обхода контура выбирают совпадающим с направлением контурного тока;
3) решают систему уравнений относительно контурных токов;
4) определяют токи в ветвях через контурные токи;
5) проверяют решения по второму закону Кирхгофа.
Метод двух узлов
Под методом двух узлов понимают метод расчета электрических цепей, в котором за искомое принимают узловое напряжение. С помощью напряжения между двумя узлами определяют токи в ветвях. На рис. 1.27 показана схема цепи с двумя узлами а и b, состоящая из четырех ветвей. Находим напряжение
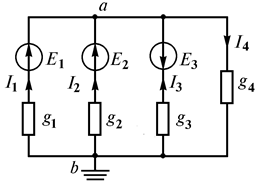 Рис. 1.27
Рис. 1.27
|
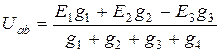 . (1.48)
. (1.48)
В общем виде напряжение между двумя узлами находят по формуле
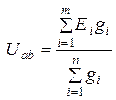 .
.
Произведение 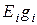 учитывается со знаком плюс, когда
учитывается со знаком плюс, когда 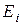 направлено к узлу, потенциал которого условно принят за более положительный (к узлу с первым индексом).
направлено к узлу, потенциал которого условно принят за более положительный (к узлу с первым индексом).
Используя напряжение между узлами 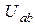 , по закону Ома определяем токи
, по закону Ома определяем токи
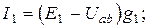
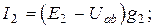
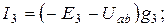
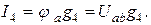
Подставим эти уравнения в уравнение, составленное по первому закону Кирхгофа
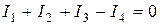 ,
,
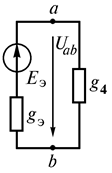 Рис. 1.28
Рис. 1.28
|
Три источника ЭДС, соединенные параллельно, можно заменить одним эквивалентным (рис. 1.28).
Из формулы (1.48) при 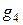 = 0 имеем
= 0 имеем
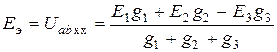
В общем виде 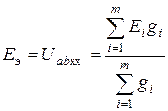 . (1.49)
. (1.49)
Число элементов уравнения (1.49) определяется количеством ветвей, содержащих ЭДС. Учитывая 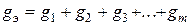 , формулу (1.49) запишем в виде
, формулу (1.49) запишем в виде
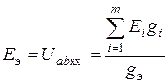 . (1.50)
. (1.50)
Пример 1.3. Для схемы на рис. 1.27 определить ток 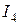 , если
, если 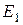 = 25 В;
= 25 В; 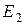 = 30 В;
= 30 В; 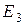 = 15 В;
= 15 В; 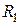 =
= 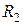 = 100 Ом;
= 100 Ом; 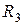 = 200 Ом;
= 200 Ом; 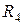 = 150 Ом.
= 150 Ом.
Решение. Напряжение между двумя узлами (1.48)
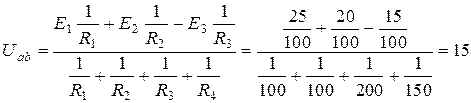 В.
В.
Ток
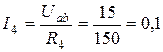 А.
А.
Принцип наложения
Принцип наложения представляет собой частный случай известного из физики принципа независимости действия сил. Сущность принципа наложения заключается в том, что в любой ветви линейной цепи с постоянными сопротивлениями равен ток алгебраической сумме частичных токов, создаваемых в этой ветви каждой из ЭДС в отдельности. Таким образом, при определении токов в ветвях можно поочередно оставлять в схеме по одной ЭДС, считая, что все остальные ЭДС равными нулю, но оставляя их внутренние сопротивления (рис. 1.29). Обычно получается цепь с последовательно-параллельным соединением сопротивлений. В этой цепи сначала определяются так называемые частичные токи, вызванные действием только первого источника ЭДС. Их обозначают 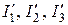 и т.п. Таким же образом рассчитывают частичные токи (
и т.п. Таким же образом рассчитывают частичные токи ( 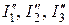 и т.д.), вызываемые действием второй ЭДС.
и т.д.), вызываемые действием второй ЭДС.
Алгебраически сложив частичные токи, определяют действительные значения токов в каждом участке сложной цепи, когда все ЭДС действуют одновременно.
Токи в ветвях 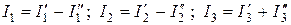 .
.
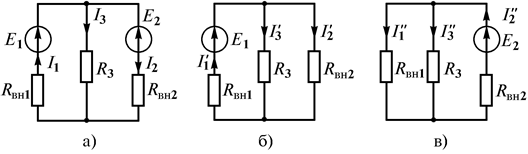
Рис. 1.29
Порядок расчета по принципу наложения:
1) поочередно рассчитывают частичные токи, возникающие от действия каждого источника, мысленно удаляя остальные из схемы, но оставляя при этом их внутренние сопротивления;
2) определяют токи в ветвях алгебраическим сложением частичных токов.
Следует отметить, что принципом наложения нельзя пользоваться для расчета мощностей, так как мощность – квадратичная функция тока или напряжения. Например,
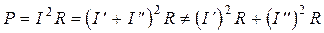 .
.
Дата добавления: 2017-01-16; просмотров: 4501;











