Получение желаемого угла набора /потери при повороте ствола.

В этом случае, мы знаем кривизну, курсовую длину, изменение угла при предыдущем измерении и желаемое изменение угла при следующем. Мы вычисляем изменение угла. По доске мы находим оценку изменения направления и ориентацию относительно оси.

Вычислите курсовую длину, необходимую для получения требуемых результатов измерения. В этом случае, мы знаем желаемые величины наклона и направления в конце курсовой длины неизвестной величины. Мы знаем угол отхода в настоящий момент, новый угол отхода и изменение направления. С помощью этих величин мы находим кривизну по ойия-доске. Зная кривизну (из предыдущих измерений), мы можем вычислить требуемую курсовую длину. На доске так же определена и ориентация относительно оси.

Вычислите новые ожидаемые величины наклона и направления при данной ориентации относительно оси и кривизне ствола.

Зная ориентацию и курсовую длину, можно вычислить изменение направления. Таким образом, мы знаем предыдущее изменение угла, ориентацию относительно оси и изменение направления. Новое изменение угла и изменение направления определяются по доске. Зная изменение направления, легко найти ожидаемое направление ствола.

Вычисления отклонения инструмента.

Основные формулы, на которых основан метод ойия-доски перечислены ниже. Все они могут быть выведены из векторной диаграммы, представленной на рис. 6.7, с помощью простых тригонометрических функций.

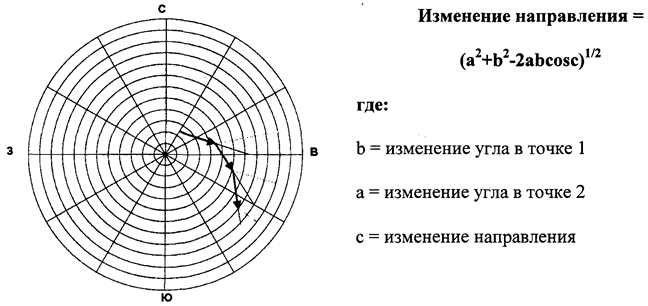
Рис. 6.9

Установка ориентации относительно оси.

1. Еслиb>а, т. е угол теряется вдоль курсовой длины, то

TF = 180° - tg^-1 asinc(b - acosc)^-1

2. Еслиb<а, т.е. угол набирается вдоль курсовой длины, то

TF= tg^-1 asinc (acosc - b)^-1

Ожидаемое изменение направления ствола.

с = tg^-1×(изменение направления × sin (ориентация отн. оси) (b + (изменение направления) × cos(opиeнтaция относительно оси)))^-1

Максимально возможное изменение направления.

C_max = sin^-1 (изменение направления) (изменение угла)^-1

Рэгланд-диаграмма

Результат различной установки ориентации инструмента относительно оси можно визуально проследить, нанося на бумагу с полярными координатами результаты измерений в каждой точке наклона и направления. Этот метод известен как Рэгланд-диаграмма (рис. 6.9). Концентрические окружности, разделенные равными промежутками, представляют собой изолинии равного наклона. Длина линии, соединяющей две точки измерения на диаграмме, является изменением направления между двумя этими точками. С помощью этой диаграммы можно наглядно проследить за способностью к отклонению от направления инструмента в зависимости от ориентации относительно оси. И наоборот, поскольку диаграмма имеет шкалу, мы можем предсказать результат отклонения направления в зависимости от ориентации инструмента при заданной кривизне (при условии, что величина реактивного момента нам известна).