Характеристика квантовых чисел
| Квантовые числа | Возможные значения | Число значений | Определяют |
| Главное n | 1,2,3… ∞ | ∞ | Среднее расстояние электрона от ядра или размер электронного облака; энергетический уровень |
| Орбитальное ℓ | 0,1,2,3…….(n-1) | n | Форму электронного облака; энергетический подуровень (S,p,α,f….) |
| Магнитное mℓ. | -ℓ….0….+ ℓ | 2 ℓ+1 | 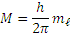 ; пространственную ориен-тацию электронного облака ; пространственную ориен-тацию электронного облака
|
| Cпиновое mS. | + 1/2 | Собственный момент количества движения электрона. |
С увеличением значений n и ℓ энергия электрона возрастает. Состояния электрона с одинаковым значением энергии называют вырожденными, а число таких состояний- степенью или кратностью вырождения.
Волновая функция при определенных значениях трех квантовых чисел(n,ℓ и mℓ) φnℓmℓ описывает состояние электрона при его орбитальном движении, которое называют атомной орбиталью (АО). Волновую функцию, зависящую от всех четырех квантовых чисел, называют спин-орбиталью.
Каждой АО соответствует область пространства определенного размера, формы и ориентации, равноценная понятию электронного облака. С целью упрощении оба эти понятия отождествляются, и когда говорят о форме АО или об электроне, находящемся на АО, то имеется в виду не сама волновая функция, а только то, что она определяет – форма электронного облака и энергетическое состояние электрона.
Число АО в пределах энергетического подуровня определяется числовым значением магнитного квантового числа (2 ℓ+1). Число АО в пределах всего энергетического уровня равно сумме АО всех его подуровней:
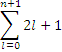
Вероятность обнаружения электрона даже на больших расстояниях от ядра только приближается к нулевому значению, поэтому электронное облако не имеет четких границ. В связи с этим введено понятие граничная поверхность, т.е. поверхность с равной электронной плотностью, ограничивающей объем, который включает 90% заряда и массы электрона. Форма и размер граничной поверхности считаются формой и размером электронного облака.
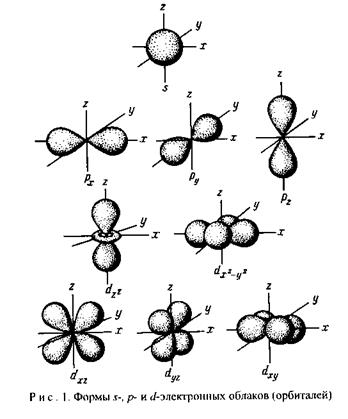
Графики радиального распределения вероятности нахождения электрона в атоме дают возможность определить форму электронных облаков. S-Электронное облако (ℓ=0) обладает сферической симметрией. р-электронное облако (ℓ=1) имеет осевую симметрию и форму, схожую с объёмной восьмеркой или гантелью. Относительное пространственное положение электронных облаков p-подуровня определяется осями координат, вдоль которых они вытянуты, поэтому для них приняты обозначения: рх , рy , рz, d-электронные облака (ℓ=2) имеют более сложную форму.
Последовательное распределение электронов в атоме по мере увеличения значений n и ℓ при данном n выражается электронными формулами или электронными конфигурациями. В первом случае энергетические уровни обозначают цифрами, а подуровни- буквами с верхним индексом, указывающим число электронов. Во втором случае атомные орбитали условно обозначают квантовыми ячейками □ , а электроны – векторами, что дает возможность показать различие в ориентации их спинов: ↑ и ↓ . Так, строение атома фтора выражается электронной формулой 1s2 2s2 2p5 электронной конфигурацией:
| 2p | ↑↓ | ↑↓ | ↑ | |||||||
| 2s | ↑↓ | |||||||||
| 1s | ↑↓ | |||||||||
Так как химическая характеристика элемента определяется прежде всего строением внешнего, а затем предвнешнего электронного слоя, то часто ограничиваются электронными формулами или конфигурациями только этих электронных слоев.
Заполнение АО в многоэлектронных атомах основано на принципе наименьшей энергии, т.е. каждый электрон занимает ту из доступных для него орбиталей, на которой его энергия будет наименьшей.
При заполнении АО действует принцип Паули, который говорит о том, что в атоме не может быть двух электронов, имеющих одинаковый набор значений для всех четырех квантовых чисел. Состояние электронов в атоме должно отличаться значением хотя бы одного квантового числа. Так, если два электрона имеют одинаковые квантовые числа n, ℓи mℓ. т.е. находятся на одной и той же АО, образуя двухэлектронное облако, то они должны отличаться значением четвертого квантового числа mS., поэтому их спины будут антипараллельными ↑↓ .
Принцип Паули определяет емкость (максимальное число электронов) энергетических уровней и подуровней, которая соответственно равна 2n2 и 2(2ℓ+1), т.е. удвоенному числу АО.
Заполнение энергетических подуровней подчиняется правилу Гунда, согласно которому электроны располагаются на вырожденных АО так, чтобы их суммарный спин был бы наибольшим, т.е. заполнение идет сначала только по одному электрону. Примером может быть р-подуровень в атомах бора, углерода и азота:
| 2s | 2p | |||
| В | ↑↓ | ↑ |
| 2s | 2p | |||
| C | ↑↓ | ↑ | ↑ |
| 2s | 2p | |||
| N | ↑↓ | ↑ | ↑ | ↑ |
В атомах элементов кислорода, фтора и неона эти АО последовательно заполняются до двух электронов.
Закономерная последовательность заполнения энергетических уровней и подуровней в атомах с увеличением порядкового номера элемента выражается правилом Клечковского, которое называют также правилом суммы n+ℓ. Согласно этому правилу порядок заполнения определяется возрастанием этой суммы , а при одинаковом ее значении первым заполняется подуровень с меньшим значением n в этой сумме:
1s→2s→2p→3s→3p→4s→3d→(n+ℓ):1+0=1 2+0=2 2+1=3 3+0=3 3+1=4 4+0=4 3+2=5
Правило Клечковского позволяет заранее предвидеть появление в периодической системе Д. И. Менделеева рядов из d-, а затем из f- элементов, которые вклиниваются между s- и p- элементами того же большого периода. Правило позволяет также предсказать структуру пока еще не существующих периодов.
Пример 1.Составьте электронные формулы атомов элементов с порядковыми номерами 16 и 22. Покажите распределение электронов этих атомов по квантовым (энергетическим) ячейкам.
Решение. Так как число электронов в атоме того или иного элемента равно его порядковому номеру в таблице Д. И. Менделеева, то на основании вышеизложенного для элементов №16 (сера) и №22 (титан) электронные формулы имеют вид
16S 1S2 2S2 2P6 3S2 3P4
22TI 1S2 2S2 2P6 3S2 3P6 4S2 3d2 , а распределение электронов по энергетическим ячейкам следующее:
| s | p | d | |||||||
| n=3 | ↑↓ | ↑ | ↑ | ||||||
| n=2 | ↑↓ | ↑↓ | ↑↓ | ↑↓ | |||||
| n=1 | ↑↓ |
| s | p | d | f | |||||||||||||
| n=4 | ↑↓ | |||||||||||||||
| n=3 | ↑↓ | ↑↓ | ↑↓ | ↑↓ | ↑ | ↑ | ||||||||||
| n=2 | ↑↓ | ↑↓ | ↑↓ | ↑↓ | ||||||||||||
| n=1 | ↑↓ |
Дата добавления: 2019-09-30; просмотров: 669;











