Фазовые переходы второго рода. Уравнения Эренфеста.

Как уже говорилось, при фазовых переходах второго рода химический потенциал μ и его производные непрерывны, а скачком меняются вторые производные μ (*). Таким образом, при фазовых переходах второго рода не происходит скачкообразного изменения объёма, и (так как s₁=s₂) не также какого-либо поглощения или выделения тепла при таком переходе. По-прежнему существует кривая p(T), при переходе через которую происходит фазовый переход, но это теперь не кривая равновесия (сосуществования) двух фаз, а кривая фазового превращения, так как при таком переходе новая фаза появляется сразу во всём объёме. О таких переходах говорят также как о непрерывных переходах, а о переходах второго рода – как о переходах, когда скачки конечны. Непрерывный переход может быть и с бесконечным разрывом.

Фазовые переходы второго рода чаще всего связаны со скачкообразным изменением каких-либо свойств симметрии тела. Например, в центрированной кубической решётке узлы, находящиеся в центрах ячеек, испытывают далее сколь угодно малое смещение, симметрия решётки меняется скачкообразно. Другой пример: при переходе магнетика из ферромагнитного состояния в парамагнитное скачком изменяется симметрия в расположении магнитных моментов. Эти примеры показывают, что скачкообразное изменение симметрии в точке фазового перехода связано с перемещением весьма малого числа атомов, или с их перемещением на весьма малые расстояния, и поэтому эти перемещения не приводят к заметным затратам энергии или к изменению объёма.

Ясно, что уравнение Клапейрона-Клаузиуса (5) здесь не работает, так как справа имеем неопределённость 0/0. Однако, нетрудно получить формулу для кривой превращения p(T). Продифференцируем равенства s₁=s₂ и 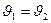вдоль кривой перехода (превращения), p и T – независимые переменные.

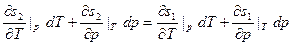
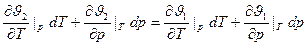
Отсюда:

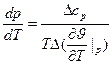(7) и эквивалентно

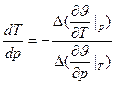(7’)

Δ – скачок из состояния один в состояние 2

Исключив 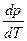, имеем:

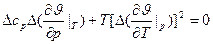(8)

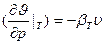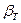, - изотермическая сжимаемость

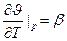- тепловое расширение

Совокупность уравнений (7) и (8) (или (7’) и (8)) носит название уравнений Эренфеста – замена уравнений Клапейрона-Клаузиуса для переходов второго рода.

Примеры фазовых переходов второго рода: парамагнетик↔ферромагнетик при температуре Кюри, диэлектрик↔сегнетоэлектрик, жидкий гелий↔сверхтекучий гелий, проводник↔сверхпроводник.