Метастабильные состояния.

Фазовые переходы.

Рассмотрим процесс (равновесный) перехода из одной фазы в другую.

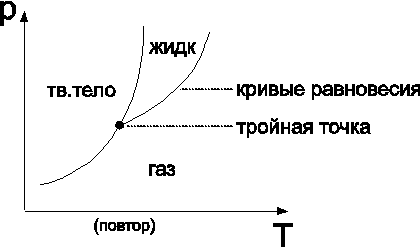
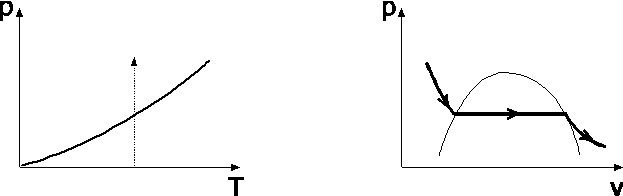Переход через кривую равновесия изображён на (p,T) и (p,V) плоскостях. Ясно, что проходит через кривую равновесия, на которой 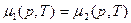(14)

Вспомним:

p₁=p₂ T₁=T₂

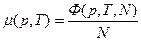(1)

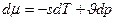
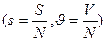
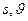- энтропия и объём на 1 моль (или на одну частицу, нам применять лучше макрочастицу, моль)

Отсюда (при N=const):

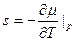
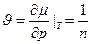(2)

n – плотность числа частиц

Так что же меняется при фазовом переходе? Ясно→ (твёрдое тело – жидкость – газ, очевидно, меняется и s при этом!!!)

Фазовые переходы, при которых меняются скачком производные химического потенциала по p и T (равные удельной энтропии и удельному объёму) называются фазовыми переходами первого рода!!!

Изменение энтропии скачком означает, что, например, переход от фазы «1» к фазе «2» сопровождается выделением тепла.

Процесс обратимый, равновесный:

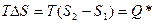или в расчёте на одну частицу (N=const!!!)

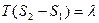(3), где

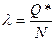- удельная или молярная (как отнормируем) теплота перехода

Таким образом, при фазовых переходах второго рода:

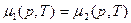, но

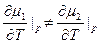
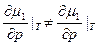(4)

Переходы первого рода: испарение, плавление, кристаллизация, возгонка.

Фазовые переходы второго рода. При них производные химического потенциала меняются непрерывно, в (4) ≠ нужно заменить на =. Нет скачков 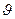и s. Но резкие скачки претерпевают вторые производные химического потенциала: теплоёмкость, тепловое расширение, изотермическая сжимаемость.

(*)

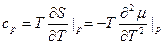
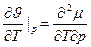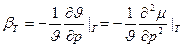
Фазовые переходы второго рода разнообразны. Многие особенности фазовых переходов второго рода присущи фазовым переходам вблизи критической точки.

Вернёмся пока к фазовым переходам первого рода.

Возьмём (14) и продифференцируем по T:

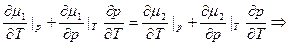
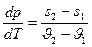или

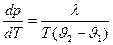(5) – уравнение Клапейрона-Клаузиуса

Оно определяет изменение давления находящихся в равновесии фаз при изменении температуры или (при интегрировании) – кривую равновесия. Та же формула в виде:

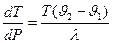(6)

Определяет изменение температуры фазового перехода при изменении давления (например, точка замерзания или кипения)

(5) и (6) показывают, что зная уравнение состояния каждой фазы и λ(T), можно найти кривую равновесия p(T).

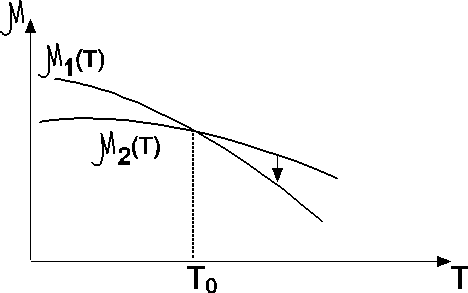
Пусть (см. рис.) p=const, и кривые 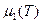и 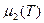соответствуют разным фазам. При этом 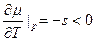и 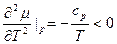для каждой фазы. Равновесие возможно при 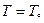, при остальных T – либо одна, либо другая фаза. Так как при фиксированных p и T устойчива система с minФ, то при 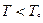устойчива первая фаза, при 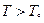- вторая. (или 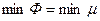). Если мы выведем систему из состояния равновесия, повысив температуру обеих фаз, то первая фаза станет неустойчивой, и (как раньше говорили) возникнет поток частиц из первой фазы во вторую (стрелка). s₂>s₁. Поэтому 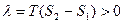, то есть происходит поглощение тепла, препятствующее повышению температуры.

Принцип Ле-Шателье: при внешнем воздействии, выводящем систему из равновесия, стимулируются процессы, стремящиеся ослабить результаты этого воздействия и стремящиеся вернуть систему в исходное состояние.

Таким образом, если будем подводить тепло (при p=const), то 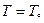до тех пор, пока всё не перейдёт во вторую фазу, то есть всё будет тратиться на фазовый переход. Процесс пойдёт по красной кривой.

Примеры (следствия (5), (6)):

1)испарение λ>0 ( )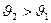

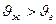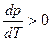
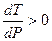- температура кипения растёт с давлением

2) плавление λ>0 и, как правило, 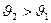( 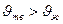) как на рис.1, и .

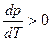Но бывает 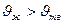( 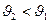) и тогда 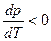как на рис.1а.

Метастабильные состояния.

Обычная точка фазового перехода не представляет собой особенностей в математическом отношении для термодинамических величин. Можно ожидать, что каждая из фаз может существовать и по другую сторону перехода (см. рис.2). Термодинамические неравенства при этом не нарушаются. Например, изотерма (пусть газ Ван-дер-Ваальса).

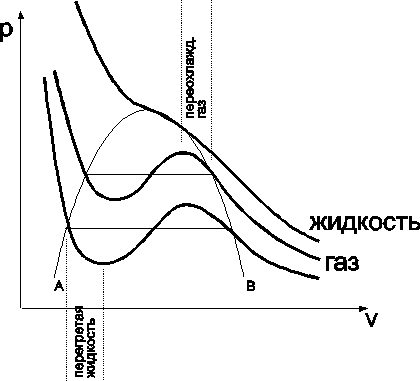
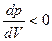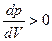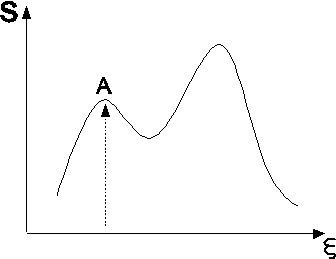
Здесь участки ab и сd – устойчивы, и тело может жить в одной фазе ( - устойчивость можно показать, исследуя minФ). Участок bc – неустойчив ( ), а фазовый переход происходит по dl (T=const). Участки изотермы db и cl – как раз и есть те участки, где может существовать перегретая жидкость (db) и переохлаждённый пар (cl). Такие состояния называются метастабильными. Кривая АКВ - геометрическое место точек, где «оканчивается» область существования этих состояний, где неравенства, например, 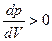, нарушаются, и тело уже не может существовать как однородное, нужно две фазы. Здесь К – критическая точка. Их относительная устойчивость может определяться отсутствием зародышей другой фазы (пузырьков, капель). Энтропия и другие термодинамические функции имеют в метастабильных состояниях локальные экстремумы.

Ясно, что maxA устойчив относительно малых флуктуаций, а достаточно большие выведут его из этого состояния (малые пузырьки газа рассасываются, а большие дают старт фазовому переходу).