Односторонние доверительные интервалы

На практике часто пользуются односторонними доверительными интервалами. Например, страховой компании не страшно, если произойдет страховых случаев много меньше среднего, но страшно, если их произойдет много больше среднего. Оценивая при покупке среднюю доходность объекта, лучше оценить ее по формуле “не меньше, чем”; при изучении среднего уровня воды в реке в областях, подверженных наводнениям, интересуются уровнем, выше которого вода не поднимется, а в областях, подверженных засухе, наоборот, уровнем, ниже которого вода не опустится.

В этом случае интервал максимально расширяют за счет одной из его границ. Если мы построим двусторонний доверительный интервал с гарантией b, а затем максимально расширим его за счет одной из его границ, то получим односторонний интервал с большей гарантией b’=b+(1-b)/2=(1+b)/2. Например, если b=0,90, то b’=0,90+0,10/2=0,95, а если b=0,95, то b’=0,95+0,05/2=0,975. Таким образом, “односторонний” подход позволяет увеличить уровень доверия, вернее, вдвое снизить ошибку a=1-b (рис. 3.12) (или при том же уровне доверия сузить интервал – вместо t_bможно взять t_2b-1) (рис. 3.13).

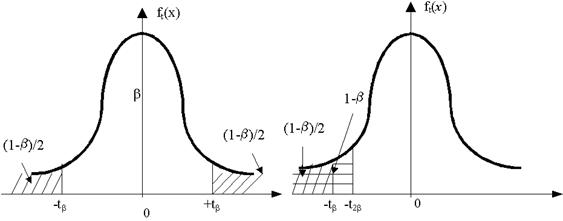
Рис. 3.12 Рис. 3.13

Если при построении двусторонних доверительных интервалов надо было решать уравнение

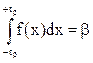, (3.19)

то для построения односторонних доверительных интервалов надо решать уравнения:

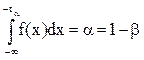, (3.19а)

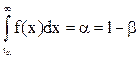. (3.19b)

Здесь f(x), как для нормального распределения, так и для распределения Стьюдента, – симметричная функция (f(x)=f(-x)), следовательно, для них ошибка, состоящая в непопадании в доверительный интервал, симметричный относительно математического ожидания, делится поровну между попаданием в полуинтервал [-¥,-t_b] и полуинтервал [t_b,¥], то есть вероятность каждого такого полуинтервала вдвое меньше ошибки двустороннего интервала. Следовательно, для поиска нужного kbпри построении одностороннего интервала надо по заданному уровню доверия b найти его ошибку a=1-b, затем удвоить ее, взять a’=2a, вычислить для нее новый уровень доверия b’=1-a’ и найти k_bдля двустороннего интервала с таким уровнем доверия. Таблицы 5 и 6 используют это обстоятельство и содержат значения половинных ошибок, позволяющих прямо по ним получать нужную квантиль (см. ниже). В таблице 6 одна и та же t соответствует ошибке двустороннего интервала, задаваемой в верхней строке таблицы, и ошибке одностороннего интервала, задаваемой в нижней строке таблицы (она вдвое меньше). В таблице 5, менее перегруженной информацией из-за отсутствия параметра n (число степеней свободы), для значения ошибки одностороннего интервала отведен свой столбец (опять же она вдвое меньше ошибки двустороннего интервала). Очень часто статистические таблицы составляются именно для односторонних интервалов. Этот способ является универсальным, а для несимметричных распределений – единственно возможным. Значения up, для которых выполняется 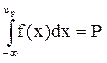, называются квантилями уровня Р. В частности, медиана есть квантиль уровня 0,5. В нашем руководстве для симметричных распределений – нормального и Стьюдента – приведены более удобные таблицы, избавляющие от выполнения даже таких несложных операций, как вычитание из 1 и деление на 2.

Ниже мы рассмотрим примеры и на односторонние интервалы. А пока приведем формулы для односторонних интервалов, соответствующие формулам (3.15) и (3.17) двусторонних интервалов:

- односторонние доверительные интервалы для математического ожидания m нормального распределения с уровнем доверия b для случая, когда среднеквадратическое отклонение распределения s известно:

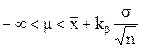(3.15a)

и

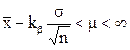, (3.15b)

k_bможно отыскать в таблице 5 по a=1-b, находя его значение в 3-м столбце;

- односторонние доверительные интервалы для математического ожидания m нормального распределения с уровнем доверия b для случая, когда среднеквадратическое отклонение распределения s неизвестно:

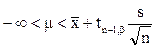(3.17a)

и

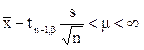, (3.17b)

t_n-1,bможно отыскать в таблице 6 по a=1-b, находя его значение в нижней строке.