Материалы лабораторных работ
ТЕМА : Изучение размерно-возрастной структуры популяции рыб.
ЦЕЛЬ : Проведенные расчеты позволяют вести учет и анализ выловленной рыбы, получить материалы по состоянию отдельных популяций рыб в водоеме, их численности, урожайности отдельных поколений, естественной смертности и др.
ЗАДАНИЕ: На основе данных массовых промеров рыб определить:
1 среднюю длину рыб
2 среднюю массу рыб
3 ихтиомассу каждого возрастного класса
4 рыбопродукцию
5 годовой прирост ихтиомассы.
ХОД РАБОТЫ:
Для суждения о размерно-возрастной структуре отлавливаемых рыб берется проба массовых промеров и проба на возраст.
Проба массовых промеров - это промер нескольких тыс.рыб подряд (без выбора крупных и мелких), что бы иметь представление о размерах рыб в видовых популяциях. Всех рыб затем взвешивают.
В пробу на возраст отбирают 25 или 50 экз. каждого размерного класса у всех видов. У ерша размерные классы через 1 -2 мм, у мелко частиковых рыб 0.5-1см, у мелкой щуки 2-Зсм, у крупной 5см.
Определив возраст рыб в пробе, приступают к распределению одноразмерных рыб в ней по возрастным классам, но предварительно распределив всех рыб в улове в соответствии с общей пробой из улова, составляя пропорции (табл. 1).
Проба массовых промеров.
| Длина рыб, см | |||||||||||
| Масса рыб, r | 3.6 | 5.8 | 8.9 | 12.9 | 18.0 | 24.2 | 31.9 | 41.1 | 51.96 | 64.57 | 79,1 |
| Количество, экз |
| Длина рыб, см | |||||||||||
| Масса рыб, г | 95.8 | 114.7 | 136.0 | 160.0 | 186.6 | 216.2 | 248,7 | 284.5 | 412,6 | ||
| Количество, экз | - | - |
Таблица 1.
Размерно-возрастная структура пробы рыб (окуня) на возраст (верхняя цифра количество рыб, нижняя-их % распределение
по возрастным классам)
| Длина см | возрастные классы | Кол-во экз. | ||||||||
| 1+ | 2+ | 3+ | 4+ | 5+ | 6+ | 7+ | 8+ | 9+ | ||
| - | ||||||||||
| - | ||||||||||
| - | ||||||||||
| - | ||||||||||
| - | - | - | ||||||||
| - | - | - | - | |||||||
| - | ||||||||||
| - | - | . | ||||||||
| - | - | |||||||||
| - | • | - | ||||||||
| - | ||||||||||
| Кол-во ЭКЗ. |
В соответствии с таблицей N 1 в пробе на возраст, рыбы размером до 7 см относятся только к возрасту 1+. В пробе массовых промеров рыбы до 7 см представлены-564 экз. Рыбы длиной 8 см относятся к двум возрастным классам - 1+ и 2+, но 90% относятся к возрасту 1+ и 10% - к возрасту 2+. После заполнения табл. N 1 распределяют массовые промеры окуня по возрастным классам.
Таблица 2.
Распределение пробы массовых промеров рыб (окуня) по возрастным классам.
| Размер рыбы, см | Доля | Число | |||||||||||||||||
| Воз | рыб в | рыб в | |||||||||||||||||
| раст | классе | пробе% | |||||||||||||||||
| 1+ | 226.8 | 824.69 | 73.2 | ||||||||||||||||
| 2+ | 25.2 | ||||||||||||||||||
| 3+ | |||||||||||||||||||
| 4+ | |||||||||||||||||||
| 5+ | |||||||||||||||||||
| 6+ | |||||||||||||||||||
| Кол- | |||||||||||||||||||
| во | |||||||||||||||||||
| рыб |
Аналогичным образом заполняется табл.З.
Таблица 3.
Массово-возрастная структура пробы окуня на возраст (верхняя цифра количество рыб, нижняя их % распределение
по возрастным классам)
| возрастные классы | Количество | ||||||||
| Масса | Экз. | ||||||||
| г | 1+ | 2+ | 3+ | 4+ | 5+ | 6+ | 7+ | ||
| 3.6 | |||||||||
| 5.8 | ' | ||||||||
| 8.9 | |||||||||
| 12.9 | |||||||||
| 17.9 | |||||||||
| 24.2 | |||||||||
| 31.9 | |||||||||
| 41.1 | |||||||||
| 51.9 | |||||||||
| 64.5 | |||||||||
| 79.1 | |||||||||
| 95.8 | |||||||||
| 114.7 | |||||||||
| 136.1 186.6 | |||||||||
| 216.2 | |||||||||
| 248.7 | |||||||||
| 284.5 | |||||||||
| 323.6 | |||||||||
| 366.2 | |||||||||
| 412.6 | |||||||||
| 462.7 | |||||||||
| 516.9 | |||||||||
| 575.3 | |||||||||
| 777.3 | |||||||||
| Кол- | |||||||||
| во экз |
После распределения пробы массовых промеров по возрастным классам определяются средняя длина и масса рыб разного возраста.
Например, средняя длина рыб возраста 1+ рассчитывается так :
Lcp.1+ = ((6* 1 1 )+(7*31 )+(8* 18)+(9*5)+( 10* 1 )+( 1 1*1))/67 = 5,92см.
Полученные данные "ю отдельным видам сводятся в облую таблицу (табл.4), где ихтиомасса возрастного класса есть произведение
средней массы одной особи в классе на количество рыб в возрастном классе, например В1 = ml * N1
( 7.3* 31951 = 232.0 ), где
В1 - ихтиомасса годовиков
ml - средняя масса годовиков;
N1 - количество годовиков
Рыбопродукция - произведение полусуммы численности рыб в смежных возрастных классах на годовой прирост массы 1 рыбы.
Например
Р1-2 = (N1 +N2)/2 * (m2 - ml), где
Р1-2 - продукция за период от годовиков до 2-х годовиков N2 и m2 - масса 2-х годовиков
Р1-2 = (31951+9840)/2 *11.3 = 235.9 кг
Годовой прирост выживших рыб - это произведение прироста массы 1 особи на численность особей в классе
Р' =(m2-m1)*N2=11.3*9804=110.8 кг
1+-2+
Таблица 4. Размерно возрастная структура популяции окуня'.
| Воз ра-ст | Длина см | Масса г | Прирост за год | Количество рыб, экз. | Ихтио масса кг | Рыбо-продукция кг | Год. прирост ихтиомассы гыживших рыб, кг | ||
| в пр.на возраст | в пр.мас промеров | в попу ляции | |||||||
| 1+ 2+ | 5.92/( 6-11) | 7.3/ (3.6-24.2) | 31951 9804 | 232.0 | 235.9 | 110.8 | |||
| 3+ | |||||||||
| 4+ | |||||||||
| 5+ | |||||||||
| 6+ | |||||||||
| 7+ | - | ||||||||
| Ито го |
' Количество рыб в популяции в данном примере не рассчитывается.
Над чертой - количество рыб, подчертой-их % распределение по возрастным классам.
Тема: "Расчет коэффициентов естественной смертности у
рыб"
Цель: С помощью проведенных расчетов можно определить характер процессов формирования численности и ихтиомассы различных возрастных групп промыслового стада рыб. Коэффициент естественной смертности есть главный биологический критерий при установлении оптимальной нормы изъятия.
Часть 1. Расчет коэффициента естественной смертности
рыб по П.В. Тюрину.
Задание 1.
На основе номограмм "Нормальных кривых переживания и темпов естественной смертности рыб как теоретической основы регулирования рыболовства" П.В. Тюрина определить коэффициент естественной смертности рыб.
Введение
При разработке методов оценки коэффициентов естественной смертности у рыб обычно исходят из 2-х различных теоретических концепций.
Одна из них основана на представлениях о том, что в в интенсивно облавливаемых популяциях рыб возрастной ряд промыслового стада укорочен, а составляющие его особи обладают близким физиологическим состоянием и одинаковыми адаптационными возможностями. Темпы естественной смертности такого промыслового стада во всех возрастных группах примерно одинаковы и не зависят от его структуры (Тюрин, 1962, 1963, 1968; Борисов, 1976; Засосов, 1976).
Согласно другой концепции (Северцов, 1941; Гулин, 1970, 1974; Тюрин, 1972) темпы естественной смертности у рыб, наряду о видовым свойством, рассматриваются как функция возраста.
Тюриным Л. В. разработаны кривые переживания различных рыб, включая древних. Кривые имеют вид параболы. Показатели ассиметрии кривых темпов естественной смертности у рыб находятся в пределах 35:65 с некоторыми колебаниями в ту или иную сторону. Для построения кривой тэмпов естественной смертности вида необходимо иметь три точки, из которых две крайние отражают очень высокую смертность на первом году жизни и в конце жизненного цикла, а третья соответствует наименьшей смертности в центре средних возрастных групп. Логарифмические номограммы по древним рыбам позволили Тюрину Н.В. разрешить этот вопрос при помощи нахождения "теоретического" предельного возраста рыб, которому бы соответствовал искомый наименьший коэффициент смертности.
ХОД РАБОТЫ
Пример расчета естественной смертности древнего "хозарского" судака по П. В. Тюрину (табл. 1).
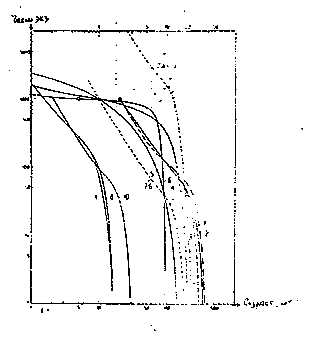
Из таблицы 1 видно, что наблюденный ряд судака по числу рыб мал (65 экз.) и имеет ступенчатый, неровный характер (колонка 2), поэтому он переводится в % на пробу в 1000 экз. (колонка 3) и затем "выравнивается" методом средних скользящих значений по трем смежным возрастным группам (колонка 4). Далее основные ("опорные") значения, определяющие вершину кривой и место ее перегиба наносятся на логарифмическую номограмму (рис. 1) и по ним вычерчивается кривая регресии, причем направление правой (нисходящей) ветви определяется по предельному фактическому возрасту в пробе или по данным литературы.
|
рис. 1. "Нормальные" кривые переживания на логарифмической номограмме:
1-сосна; 2-лиственница сибирская; 3-береэа; 4-морской котик; 5-волк; б-человек. (Швеция); 7А, РБ-голец-намайкуш;
7 (жирные точки)-продолжение линии регресии по Кеннеди; 8-"хоэарский" судак; 9-древний судак на рубеже старой и новой эры; 10-"хозарский" сом (ордината число экземпляров, абцисса-возраст в годах; внизу для древних рыб, человека и деревьев; вверху-для намайкуша. морского котика и волка).
Таблица 1 Численность и темпы естественной смертности
хозарского судака
| Возраст, годы | Число экземпляров | То же в % | Выравнено по 3х-годовым скользящим значениям | По логарифмической номограмме | ||
| Численность экз. | Смертность экз. | К ест.см % | ||||
| - | - | - | - | - | - | |
| - | - | - | - | - | ||
| - | - | - | ||||
| - | ||||||
| - | - | - | ||||
| - | ||||||
| - | ||||||
| - | - | - | 31,5 | |||
| - | 37,5 | |||||
| - | 46,5 | |||||
| - | - | - | 7,2 | 8,8 | ||
| - | - | - | 2,4 | 4,8 | ||
| - | - | - | - | - | - | |
| Расчётная проба | - | - | - | - |
Смертность рыб (колонка 6) определяется как разность между численностью смежных возрастных групп. Коэффициент естественной смертности определятся отношением смертности к количеству рыб в данной возрастной группе в %.
Например, для двухгодовиков: 917 : 1650 = 5,6 x 100 = 56 %
Из таблицы 1 следует, что наименьший показатель годовой еотественной смертности "хозарского" судака (18%) приходится на возраст 5,5-6,5 в среднем 6 лет. При предельном возрасте судака 17 лет (Бойко, 1964) показатель ассиметрии кривой темпов естественной смертности составил 6:17 = 35:65.
Задание 2.
Рассчитать коэффициент естественной смертности судака Цимлянского водохранилища (табл. 2). Известна средняя численность судака по учету запасов (Лапицкий, 1970) в тыс. шт., которая трансформирована (в промилле) на пробу в 1000 экз. Наименьший показатель естественной смертности определяется по таблице и графику П.В. Тюрина.
Таблица 2
Расчет темпов общей, естественной и промысловой смертности судака Цимлянского водохранилища
| Возраст | Средняя численность по учёту запасов | Нормальные показатели смертности, % | ? ест. Смертности , % | Действительные показатели смертности % | |||||
| Тыс. шт. | %. | Выр-е по лог. Гр. | Общая | Ест. | Пром. | Ест. | Пром. | ||
| 0+ | - | - | (90) | - | - | - | |||
| 1+ | (2540) | (65) | 0,64 | 63,2 | 1,64 | ||||
| 2+ | (890) | (49) | -2 | ||||||
| 3+ | (455) | (44) | -4 | ||||||
| 4+ | -6 | ||||||||
| 5+ | -5 | ||||||||
| 6+ | -5 | ||||||||
| 7+ | -4 | ||||||||
| -4 |
? ест. См =(Кест.см * Квылова)/100
От действия промысла К ест. снижается, К выл. соответственно увеличивается на величину ? ест.см. На основании полученных данных построить параболу.
Часть II. Расчет коэффициентов естественной смертности рыб по Л. А. Зыкову.
В основе способа лежат математические расчеты, связанные с ростом и половым созреванием рыб.; Предлагается, что максимальное значение кривой приходится на период полового созревания рыб, значения коэффициентов естественной смертности здесь будут минимальными.
Л.А. Зыков использует модель:
γм = 1-Аtk(Tk-tk),
где γм - коэффициент естественной смертности рыб,
k- константа уравнения роста И. И. Шмальгаузена, описываемого уравнением:
l = gtk
Связь медду массой, особи и ее возрастом описывается степенным уравнением W = Ptc,
где Р, С, К, g - константы, определяются методом наименьших квадратов, t - возраст рыбы.
Величина А определяется по уравнению:
А = (1-γmn)/ tn2k,
Где γmn = 1-1-c/tn,
где С - константа уравнения W - Ptс, γmn - смертность рыб в точке кульминации кривой естественной смертности, соответствующей времени наступления половой зрелости.
tn - возраст полового созревания 50% количества особей.
l – основание натуральных логарифмов
tn = (ln/q)1/k, где
In - длина 50% созревших рыб. Она определяется по формуле
1п = 0,5 L, где
L - максимальная теоретическая длина рыб данного вида.
Зная L, можно определить максимальный теоретический возраст рыб:
Тk = L/q = 2ln/q (L= 2ln)
Определив все составляющие модели А, проводят расчет коэфициентов естественной смертности рыб.
Задание3. Определить коэффициенты естественной смертности уральского шипа.
| Возраст | Длина, см | Масса,кг | Возраст | Длина, см | Масса,кг |
| Самцы | |||||
| 53,2 | 1,3 | 150,7 | 19,8 | ||
| 68,9 | 2,6 | 154,1 | |||
| 80,3 | 3,9 | 157,5 | 22,2 | ||
| 89,5 | 5,1 | 160,7 | 23,4 | ||
| 97,3 | 6,4 | 163,8 | 24,6 | ||
| 104,2 | 7,6 | 166,9 | 25,8 | ||
| 110,4 | 8,9 | 169,8 | |||
| 116,1 | 10,1 | 172,7 | 28,2 | ||
| 121,4 | 11,3 | 175,4 | 29,4 | ||
| 126,3 | 12,5 | 178,2 | 30,6 | ||
| 130,9 | 13,8 | 180,8 | 31,8 | ||
| 135,2 | 14,9 | 183,4 | 32,9 | ||
| 139,4 | 16,2 | 185,9 | 34,2 | ||
| 143,3 | 17,4 | 188,4 | 35,4 | ||
| 147,1 | 18,6 | 190,8 | 36,5 |
Тема: “Методы изучения запасов рыб”
Цель: Познакомить студентов с методами исследования запасов рыб, что необходимо для определения величины промыслового изъятия и сохранения численности популяции рыб на оптимальном уровне.
Часть I.
Вводная часть
Понятия запасы рыб идентично понятию “численности” рыб, также как “колебание запасов соответствует “колебанию численности” рыб.
Определение состояния запасов промысловых рыб и других водных объектов является важнейшей задачей рыбохозяйственных исследований. Благодаря ему устанавливается величина промыслового изъятия, оптимальный допустимый улов (ОДУ), планируется рациональное использование запасов и т.д.
Методы изучения запасов рыб делятся на абсолютные и относительные.
Среди абсолютных методов различают прямые (метод площадей, инструментальная схема и др.) и косвенные (мечение, анализ ежегодных данных об уловах, промысловом усилии и др.)
К относительным методам относятся биостатистический метод, разработанный в 1912 году А. Н. Державиным для каспийской севрюги. Сущность метода заключается в том, что с помощью репрезентативных выборок изучается возрастная структура промысловых уловов и на этой основе оценивается численность каждого поколения, после чего сложением количества особей во всех поколениях, представленных в улове рассматриваемого года, отыскивается минимальная (гибель рыб от естественных причин не принимается во внимание) величина промыслового запаса.
Промысловый запас определяется как сумма, состоящая из остатка после весеннего нереста, пополнения и особей, пропустивших предыдущей нерест.
Математически это записывается так:
Rа + RЬ + Rс = 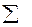 Na +
Na + 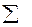 Nb +
Nb + 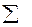 Nc
Nc
где Nа, Nb, Nс - численность соответствующих возрастных групп;
а, b, с - число лет, прожитых возрастной группой.
Недостатками метода является обязательность расчетов запаса рыб при одинаковой интенсивности промысла на многолетнем материале, а также недооценка естественной смертности рыб.
Т. Ф. Дементьева (1976) модифицировала метод А. Н. Державина. Модель построения запаса рыб по Т. Ф. Дементьевой (1976) следующая:
1) устанавливается- возрастной и размерный состав промыслового стада на
основании средних проб, собранных отцеживающими орудиями лова;
2) в результате учета рыб с нерестовыми марками определяется соотношение между остатком и пополнением;
3) определяются темпы роста и созревания основных возрастных групп (поколений), составляющих промысловое стадо и выясняются причины колебаний их численности и изменений роста;
4) оценивается предполагаемая мощность поколений на основании учета сеголетков исследовательскими орудиями лова;
5) производится расчет численности поколений и темпа использования их промыслом (промысловая смертность) на основании динамики возрастного состава и построения модели запаса по методу А. Н. Державина;
6) определяется плотность популяции в период нерестовых или зимовальных скоплений по уловам на усилие;
7) дается оценка относительной численности запаса, промыслового стада и пополнения вместе с биологическим обоснованием их формирования;
8) устанавливается коэффициент корреляции между фактическими уловами, плотностью популяции и численностью поколений, а затем посредством экстраполяции определяется величина возможного улова от запаса.
Пример расчета запаса северокаспийского леща по методу Т. Ф. Дементьевой (1976).
Приступая к оценке состояния запасов, необходимо определить величину поколений за многолетний период по возрастному составу уловов (табл. 1).
Промысловое стадо формируется осенью, после летного периода роста и облавливается обычно в течение, осени и последующей весны .В популяции леща в течении ряда лет было несколько урожайных и неурожайных поколений.
Показатели урожайных поколений выделены полужирным шрифтом.
На основании данных таблицы 1 составляется таблица 2, где определяется численность отдельных возрастных групп леща в млн. штук.
Таблица 1
Возрастной состав леща по промыслово-биологическим годам, %
| Год | Сезон | Возраст, годы | Улов, тыс. т | Средняя масса 1 экз., г | ||||||
| Осень | 14,1 | 34,0 | 11,6 | 34,7 | 4,8 | 0,6 | - | 6,0 | ||
| Весна | 0,3 | 10,6 | 12,6 | 54,3 | 19,6 | 2,4 | 0,2 | 10,1 | ||
| Осень | 32,9 | 46,5 | 6,0 | 2,6 | 8,4 | 3,2 | 0,4 | 2,7 | ||
| Весна | 16,2 | 29,2 | 26,8 | 7,8 | 15,7 | 5,2 | 0,1 | 7,8 | ||
| Осень | 2,4 | 91,0 | 6,2 | 0,4 | - | - | - | 10,0 | ||
| Весна | 0,2 | 82,1 | 13,9 | 2,0 | 0,6 | 1,2 | - | 28,1 | ||
| Осень | 0,4 | 5,0 | 89,0 | 5,0 | 0,6 | - | - | 19,0 | ||
| Весна | - | 2,0 | 91,5 | 5,6 | 0,3 | 0,3 | 0,3 | 66,4 | ||
| Осень | - | 2,3 | 13,7 | 81,5 | 2,5 | - | - | 14,7 | ||
| Весна | - | 0,8 | 25,2 | 72,4 | 1,4 | 0,1 | 0,1 | 66,5 | ||
| Осень | 1,5 | 45,6 | 16,7 | 15,1 | 20,5 | 0,6 | - | 17,1 | ||
| Весна | 1,2 | 29,8 | 23,8 | 17,6 | 26,0 | 1,4 | 0,2 | 32,7 | ||
| Осень | 13,8 | 18,2 | 50,0 | 6,4 | 4,8 | 6,3 | 0,5 | 5,9 | ||
| Весна | 4,0 | 13,4 | 56,8 | 8,5 | 5,0 | 12,3 | - | 26,0 | ||
| Осень | 2,9 | 73,5 | 18,9 | 3,6 | 0,6 | 0,4 | 0,1 | 14,0 | ||
| Весна | - | 67,2 | 20,9 | 9,3 | 1,8 | 0,2 | 0,6 | 36,6 |
Расчет ведется по формуле:
N = P / W,где
N-улов, штуки;
Р-улов в единицах массы;
W-средняя масса 1экз., г.
Например, численность всех возрастных групп леща осенью 1970 года составит:
N = 6000 т / 0.00055 т = 10,9 млн. шт.
а, например, доля двух годовиков 14,1%, или 1,6 млн. шт.
Таблица 2
Распределение леща в уловах по возрастным группам , млн.шт.
| Год | Сезон | Возраст, годы | Всего, млн. шт. | ||||||
| Осень | 1,6 | 11,0 | |||||||
| Весна | |||||||||
| Осень | |||||||||
| Весна | |||||||||
| Осень | |||||||||
| Весна | |||||||||
| Осень | |||||||||
| Весна | |||||||||
| Осень | |||||||||
| Весна | |||||||||
| Осень | |||||||||
| Весна | |||||||||
| Осень | |||||||||
| Весна | |||||||||
| Осень | |||||||||
| Весна |
Суммируя приведённые в таблице 2 данные по промыслово-биологическ<
Дата добавления: 2021-04-21; просмотров: 1046;