Типы магнетиков. Элементарная теория диа- и парамаг-нетизма.
Выделяют такие типы магнетиков, как диа- и парамагнетики.
Диамагнетики
У диамагнитных веществ суммарный магнитный момент атома равен нулю, так как имеющиеся в атоме орбитальные, спиновые и ядерные моменты взаимно компенсируются (рис. 4.3.1, а). Однако электронные орбиты атома под действием внешнего магнитного поля совершают прецессионное движение, которое эквивалентно круго-вому току. Так как этот микроток индуцирован внешним магнитным полем, то, согласно правилу Ленца, его собственное магнитное поле, а следовательно и магнитный момент направлены противоположно внешнему полю (рис. 4.3.1, б). Индуцированные магнитные моменты атомов (молекул) складываются и образуют собственное магнитное поле вещества, ослабляющее внешнее магнитное поле. Этот эффект получил название диамагнитного эффекта, а вещества, намагничи-вающиеся во внешнем магнитном поле против направления поля, на-звали диамагнетиками. Так как диамагнитный эффект обусловлен действием внешнего магнитного поля на электроны атомов вещества, то диамагнетизм свойствен всем веществам.
B
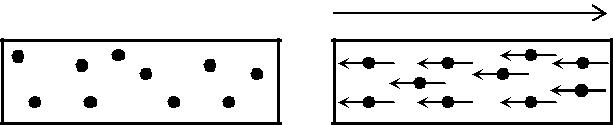
а б
Рис. 4.3.1
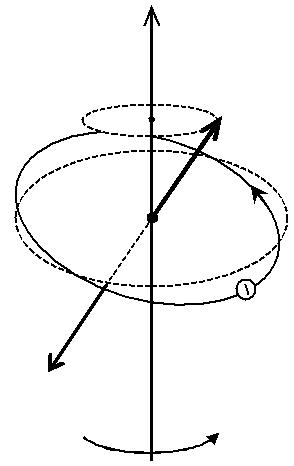
Рассмотрим намагничивание диамагнетика (рис. 4.3.2). В отсутст-вие магнитного поля (В = 0) электрон движется в электрическом поле ядра атома по вполне определенной стационарной орбите. Электрон на круговой орбите удерживается силой кулоновского притяжения к ядру. При этом электрон обладает орбитальным механическим моментом и
| ωL |
| Рис. 4.3.2 |
| B |
| pm |
| I |
магнитным моментом, которые связаны между собой гиромагнитным отношением gopб. Поскольку В = 0, оба эти вектора L0 и pm сохраняют
свое направление в пространстве (если не принимать во внимание теп-ловое движение атомов). Во внешнем магнитном поле индукцией В на электрон в атоме будет действовать вращающий момент
| M = p | m | × B . | (4.3.1) | |
е
L0 
| С учетом выражения (4.1.9) он будет равен: | |||||||||||||||||||||
| M | = − g | L | × B | . | (4.3.2) | ||||||||||||||||
| орб | |||||||||||||||||||||
| Согласно закону об изменении момента импульса получаем: | |||||||||||||||||||||
| dL | dL | ⇒ | dL | = | (4.3.3) | ||||||||||||||||
| = | M0 | ⇒ | = − | × | × | L0 | |||||||||||||||
| dt | dt | dt | |||||||||||||||||||
| g орб L0 | B | g орбB | . | ||||||||||||||||||
Уравнения (4.3.3) по виду совпадают с кинематическим выраже-нием для скорости υ движения точки твердого тела, вращающегося вокруг неподвижной оси:
| dr | (4.3.4) | ||||
| υ= dt | = ω×r | . |
Сопоставляя уравнение (4.3.4) с соотношением (4.3.3), можно придти к выводу, что вектор L0 орбитального момента импульса и связанный с ним вектор pm магнитного момента совершают в магнит-
ном поле прецессионное движение вокруг оси (рис. 4.3.2), параллель-
ной вектору B с угловой скоростью
| ωL = g орбB = | eB | . | (4.3.5) | |
| 2me |
Угловая скорость прецессии ωL совпадает по направлению с век-тором индукции В (рис. 4.3.2). Прецессионное движение электронных орбит открыл в 1895 г. ирландский физик Джозеф Лармор. Он сфор-мулировал теорему (теорема Лармора): единственным результатом действия магнитного поля на движение электрона в атоме является прецессия электронных орбит вокруг оси, параллельной магнитному полю и проходящей через ядро атома, причем модуль угловой скоро-
сти ω L = eB . А прецессионное движение электронных орбит носит
2me
название прецессия Лармора.
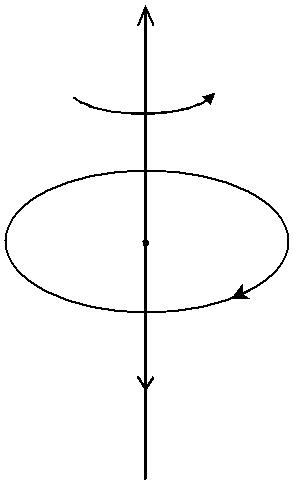
B
ωL
S⊥ Iпрец
pm
Рис. 4.3.3
Прецессия электронных орбит приводит к появлению дополни-тельного орбитального тока (рис. 4.3.3):
| I | прец | = | e | = | eω | L | = | e2 B | . | (4.3.6) | |
| T | 4πm | ||||||||||
| 2π | |||||||||||
| L | e | ||||||||||
| Этот ток создает индуцированный (наведенный) орбитальный | |||||||||||
| магнитный момент: |
| p | = | I | прец | S | ⊥ | = | e2 B | S | ⊥ | , | (4.3.7) | |||||||
| 4πm | ||||||||||||||||||
| m | ||||||||||||||||||
| e | ||||||||||||||||||
| где S⊥ – | площадь проекции орбиты на плоскость перпендикулярную | |||||||||||||||||
| вектору B. | ||||||||||||||||||
| Так как вектор pm направлен против внешнего поля, то можно | ||||||||||||||||||
| записать | e2 S | |||||||||||||||||
| ⊥ | ||||||||||||||||||
| p m = − | B. | (4.3.8) | ||||||||||||||||
| 4πme | ||||||||||||||||||
Для атома, имеющего Z электронов, общий наведенный орби-тальный магнитный момент равен:
| Ze 2 B | ||||
| pm = − | S ⊥B. | (4.3.9) | ||
| 4πme | ||||
Этот дополнительный магнитный момент приводит к возникно-вению индуцированной намагниченности , направленной против внешнего поля В. Он играет определяющую роль при объяснении яв-ления намагничивания диамагнетиков.
Найдем намагниченность диамагнетика. Вектор намагниченности диамагнетика будет равен:
| N | Ze 2 S ⊥ | Ze 2 S⊥ | ||||||||||||
| J | = lim | ∑ | pmi = − | NB = − n | B = − n | μ0 H. (4.3.10) | ||||||||
| V | 4π m | 4πm | ||||||||||||
| V →0 | V i=1 | |||||||||||||
| e | e | |||||||||||||
| Сравнивая формулу (4.3.10) с (4.2.2) получим: | ||||||||||||||
| χ = −n | Ze 2 S | ⊥ | . | (4.3.11) | ||||||||||
| 4πm | ||||||||||||||
| e |
Оценка по формуле (4.3.11) и экспериментальные данные показы-вают, что значение магнитной восприимчивости для диамагнетиков практически составляет порядка χ = –10–6.
Восприимчивость диамагнетиков почти не зависит от температу-ры Т и напряженности Н магнитного поля. Поэтому процесс намагни-чивания диамагнетиков характеризуется линейной зависимостью J
от H (рис. 4.3.4).
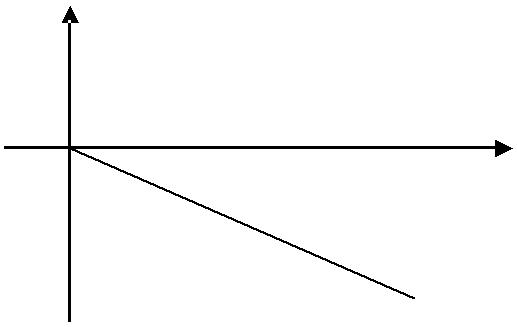
J
O
H
Рис. 4.3.4
Парамагнетики
Наряду с диамагнитными веществами существуют и парамагнит-ные – вещества, намагничивающиеся во внешнем магнитном поле по направлению поля.
У парамагнитных веществ при отсутствии внешнего магнитного поля магнитные моменты электронов не компенсируют друг друга, и
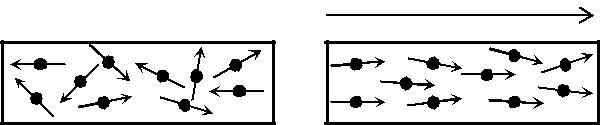
атомы (молекулы) парамагнетиков всегда обладают магнитным момен-том. Однако вследствие теплового движения молекул их магнитные мо-менты ориентированы беспорядочно (рис. 4.3.5, а), поэтому парамаг-нитные вещества магнитными свойствами не обладают. При внесении парамагнетика во внешнее магнитное поле устанавливается преимуще-ственная ориентация магнитных моментов атомов по полю (полной ори-ентации препятствует тепловое движение атомов) (рис. 4.3.5, б). Таким образом, парамагнетик намагничивается, создавая собственное магнит-ное поле, совпадающее по направлению с внешним полем и усили-вающее его. Этот эффект называется парамагнитным. При ослаблении внешнего магнитного поля до нуля ориентация магнитных моментов вследствие теплового движения нарушается и парамагнетик размагни-чивается.
J
B
а
б O
H
Рис. 4.3.5 Рис. 4.3.6
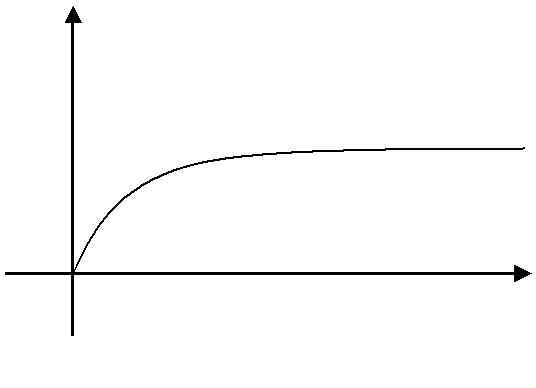
Процесс намагничивания парамагнетиков во многом аналогичен тому, как поляризуется диэлектрик, состоящий из полярных молекул. Кривая намагничивания парамагнетиков (рис. 4.3.6) указывает на яв-ление насыщения, которое связано с ориентационным упорядочением магнитных моментов молекул вещества. Классическая статистическая теория парамагнетизма была построена французским физиком Полем Ланжевеном в 1905 г. Согласно этой теории в не очень сильных одно-родных постоянных магнитных полях, когда потенциальная энергия «элементарного тока» намного меньше характерной тепловой энер-гии, восприимчивость χ парамагнетика оказывается обратно пропор-циональна температуре:
| μ | np2 | |||||
| χ= | m | . | (4.3.12) | |||
| 3kT | ||||||
Значения проницаемости χ парамагнетика лежит в пределах 10–5–10–3. Подводя итог, отметим, что атомы всех веществ являются носите-лями диамагнитных свойств. Если магнитный момент атомов велик,
то парамагнитные свойства преобладают над диамагнитными и веще-ство является парамагнетиком. Если магнитный момент атомов мал, то преобладают диамагнитные свойства и вещество является диамаг-нетиком.
Дата добавления: 2017-01-08; просмотров: 2724;











