Аналоговый сигнал (АС)

Основные сигналы в радиоэлектронике и их спектральное представление

Классификация и представление сигналов. Детерминированные, случайные; управляющие, радиосигналы. Аналоговое, дискретно-непрерывное, цифровое представление. Временное описание сигналов. Понятие, примеры: гармонический, прямоугольный, ступенчатый (единичная функция включения), короткий импульс - d -функции Дирака, ее связь с сигналом включения, фильтрующие свойства d -функции. Динамическое описание непрерывного сигнала с помощью d -функции и 1(t)-единичной ступенчатой функции. Спектральное описание сигналов. Управляющие сигналы. Периодические сигналы: математическое и физическое понятия периодического сигнала, представление суммой гармонических колебаний, ряд Фурье в действительной и комплексной форме, понятие спектра сигнала, возможность физической реализации. Периодическая последовательность прямоугольных импульсов (длительность импульса, скважность, спектр амплитуд и фаз, дискретность спектра). Распределение энергии в спектре сигнала, практическая ширина спектра. Непериодические сигналы: понятие детерминированного непериодического сигнала, интегральные преобразования Фурье, физический смысл спектральной плотности и условия абсолютной интегрируемости, непрерывность спектра; спектр сигнала включения, прямоугольного импульса, d -функции. Теоремы запаздывания, смещения, спектр произведения сигналов (свертка). Распределение энергии в спектре непериодического сигнала. Модулированные колебания, виды модулированных сигналов. Амплитудно-модулированные колебания: энергетика, спектр АМ-колебания при сложном модулирующем сигнале, ширина спектра; АМ-колебания с подавлением несущей, однополосные АМ-колебания. ЧМ и ФМ колебания, их связь, девиация и индекс модуляции, спектр при малом и большом индексе модуляции, зависимость практической ширины спектра от частоты модулирующего сигнала. Импульсно модулированные колебания, проблема выбора шага дискретизации, теорема Котельникова. Частотное и временное разделение каналов. Помехоустойчивость АМ, ЧМ, ФМ и ИМ -колебаний

Аналоговый сигнал (АС)

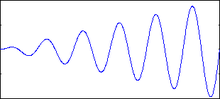
Аналоговый сигнал

Большинство сигналов имеют аналоговую природу, то есть изменяются непрерывно во времени и могут принимать любые значения на некотором интервале. Аналоговые сигналы описываются некоторой математической функцией времени.

Пример АС — гармонический сигнал: s(t) = A·cos(ω·t + φ).

Аналоговые сигналы используются в телефонии, радиовещании, телевидении. Ввести такой сигнал в цифровую систему для обработки невозможно, так как на любом интервале времени он может иметь бесконечное множество значений, и для точного (без погрешности) представления его значения требуются числа бесконечной разрядности. Поэтому очень часто необходимо преобразовывать аналоговый сигнал так, чтобы можно было представить его последовательностью чисел заданной разрядности.

Дискретный сигнал

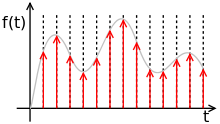
Дискретный сигнал

Дискретизация аналогового сигнала состоит в том, что сигнал представляется в виде последовательности значений, взятых в дискретные моменты времени t_i (где i — индекс). Обычно промежутки времени между последовательными отсчётами (Δt_i = t_i − t_i−1) постоянны; в таком случае, Δt называется интервалом дискретизации. Сами же значения сигнала x(t) в моменты измерения, то есть x_i = x(t_i), называются отсчётами.