Методы анализа процессов в линейных цепях (системах)

При анализе процессов в электрических цепях

необходимо определить отклик цепи на входной сигнал в виде

сигнала заданной формы. Отклик выражают в значениях напря- Г. Кирхгоф

жений u(f) и токов i(t) в разные моменты времени. Из

теоретических основ электротехники известно, что для анализа прохождения

гармонических сигналов через линейные цепи используют законы Кирхгофа (Кирхгоф

Густав — Kirchhoff Gustav, знаменитый немецкий физик; 1824—1887), методы

контурных токов, методы узловых потенциалов, метод эквивалентного

генератора и другие несложные методы. Эти методы применимы и для анализа при

произвольном воздействии на вход линейной цепи.

Однако в радиотехнике приходится иметь дело с импульсными сигналами, которые более разнообразны по форме и спектральному составу и описываются значительным числом

параметров. Кроме того, радиотехнические цепи сложны и по структуре.

При анализе воздействия сигналов на сложные по структуре цепи

применяют классический, операторный, частотный методы и метод интеграла

наложения. Классический метод основан на составлении и решении дифференциальных

уравнений и наиболее удобен для анализа прохождения импульсных сигналов

через линейные цепи. Если на сложные по структуре цепи

воздействуют сложные по спектральному составу сигналы, то для анализа

прохождения сигналов удобнее применять спектральный и операторный методы, а

также относящийся к временным методам метод интеграла наложения.

Спектральный метод. Свойства линейных цепей (линейных

четырехполюсников) можно определить с помощью такого параметра, как частотный

коэффициент передачи. Для этого необходимо рассмотреть отклик линейного

четырехполюсника на входное воздействие и оценить их связь между собой.

(подробнее на стр.360-362 Нефедов В.И. Основы радиоэлектроники )

Операторный метод. Наряду со спектральным методом в теоретической

радиоэлектронике и технике радиосвязи широко применяется очень близкий к

нему по логической структуре операторный метод, который базируется на

представлении преобразованиями Лапласа входных и выходных сигналов линейного

четырехполюсника. По существу спектральный метод является разновидностью

операторного метода, в котором операторным изображением сигналов по Фурье

служат их спектры. Однако в отличие от реальных спектров операторные

изображения сигналов в общем случае являются абстрактными математическими

моделями и понятиями, которые только упрощают анализ процессов в

радиотехнических

(подробнее на стр.362-366 Нефедов В.И. Основы радиоэлектроники )

№3 Резонансные электрические цепи и их основные свойства.

(подробнее на стр.377-383 Нефедов В.И. Основы радиоэлектроники )

Последовательный колебательный контур. Последовательный

колебательный (часто, резонансный) контур состоит из последовательно соединенных

сопротивления R, индуктивности L и емкости С (рис. 4.12, а). Обычно резистор

R определяет сопротивление омических потерь провода, из которого выполнена

индуктивность. Сопротивление потерь емкости мало, и его на практике не

учитывают.

Запишем полное входное сопротивление (импеданс — устаревшее) контура

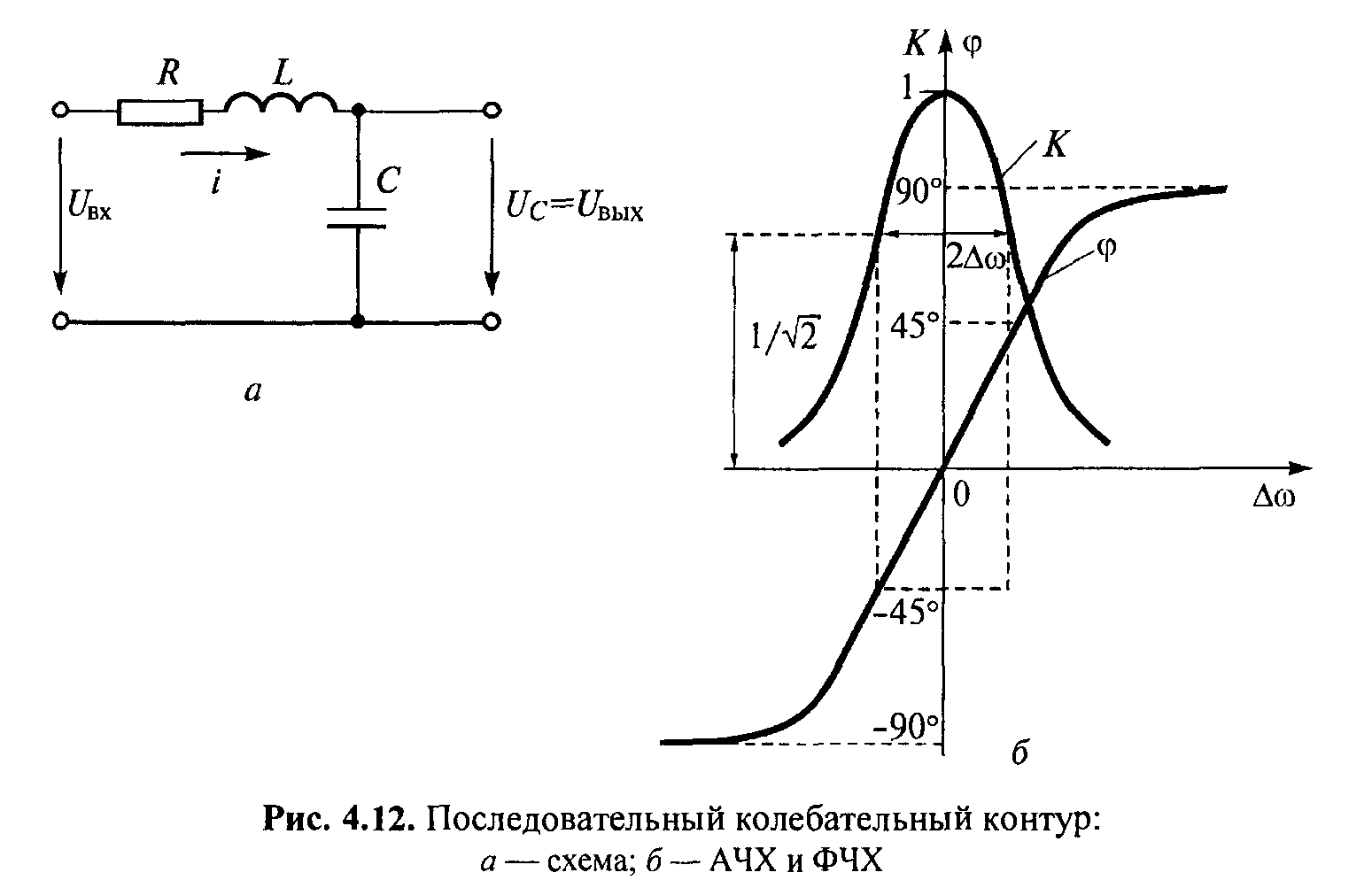
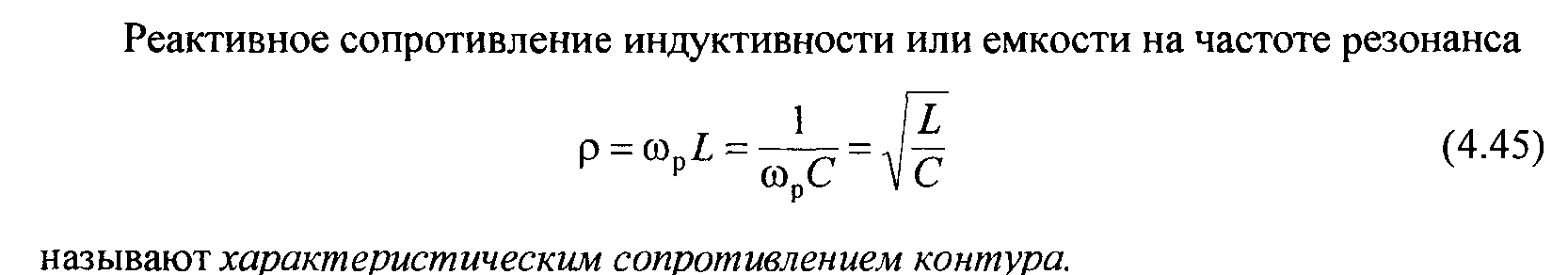
Частоту на которой реактивная составляющая входного сопротивления

равна нулю, называют резонансной (от лат. resono — откликаюсь) частотой

контура.

При настройке контура в резонанс амплитуда напряжения на

конденсаторе (или индуктивности) в Q раз больше амплитуды входного напряжения.

Поэтому резонанс в последовательном контуре называют резонансом напряжений.

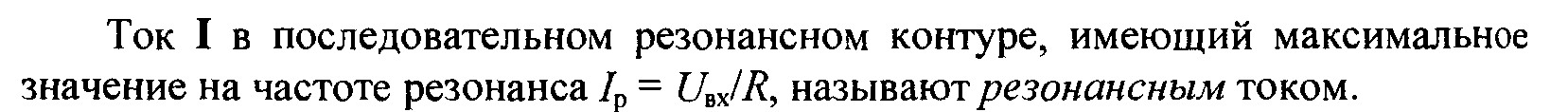
Параллельный колебательный контур. Такой контур состоит из

параллельно соединенных индуктивности L и емкости С, а в цепь индуктивности

включено сопротивление ее потерь R (рис. 4.13, а).

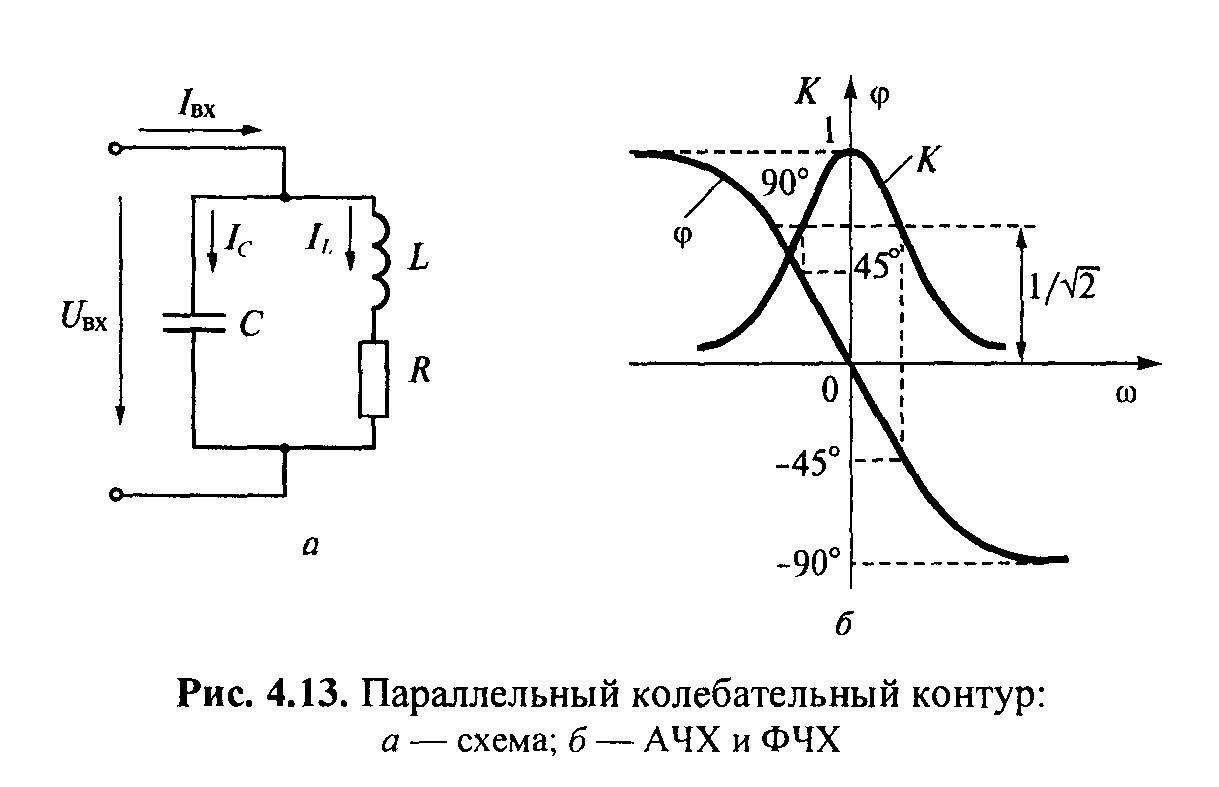
Итак, на резонансной частоте ток в параллельном контуре в Q раз больше

входного тока. Поэтому говорят о резонансе токов в параллельном контуре.

Связанные контуры. Если требуется существенно повысить частотную

избирательность радиотехнических устройств, то используют многоконтурные

линейные цепи, в которых удается получать близкую к идеальной

(прямоугольной) форму АЧХ. Простейшими многоконтурными частотно-избирательными

цепями являются два связанных колебательных контура.

Для удобства реализации связанные контуры составляют из

одинаковых элементов, а связь между ними чаще всего бывает индуктивной или

емкостной (рис. 4.15). При индуктивной связи между катушками индуктивностей

образуется взаимная индуктивность, определяемая коэффициентом взаимной

индуктивности МХне путать с глубиной модуляции).

№4 Простейшие линейные RC и RL цепи при импульсном воздействии.

Такие устройства предназначены для формирования и преобразования электрических сигналов, имеющих характер импульсов и перепадов напряжений. К импульсным устройствам относятся все цифровые микросхемы и некоторые аналоговые, например, микросхемы генераторов и компараторов. Ранее я рассматривал один из основных элементов импульсных устройств – транзистор, работающий в ключевом режиме.

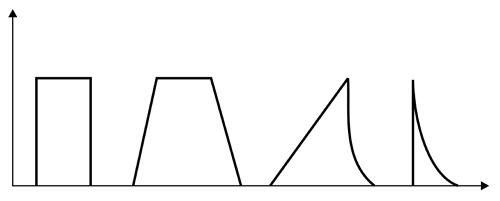
Формы импульса (слева направо): прямоугольная, трапецеидальная, пилообразная, экспоненциальная.

В радиоэлектронике используются импульсы самых разнообразных форм, но наиболее распространённые это: прямоугольные, трапецеидальные, пилообразные и экспоненциальные формы импульсов. Форма любого импульса характеризуется следующими основными параметрами:

· амплитуда (максимальное значение) импульса, U_m;

· начальное значение импульса, U₀;

· длительность импульса, t_и;

· длительность переднего фронта (или просто фронта) импульса, t_ф;

· длительность заднего фронта (или среза) импульса, t_с;

· длительность вершины импульса, t_в;

· снижение вершины импульса, Δu;

· крутизна фронта импульса (скорость изменения напряжения при формировании переднего или заднего фронта).

В случае использовании периодичности повторяющихся импульсов имеют большое значение такие параметры, как скважность импульсов (ξ или S), коэффициент заполнения импульсов (η или D), частота повторения импульсов (f) и период повторения импульсов (T). Данные параметры имеют следующие соотношения между собой

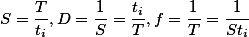
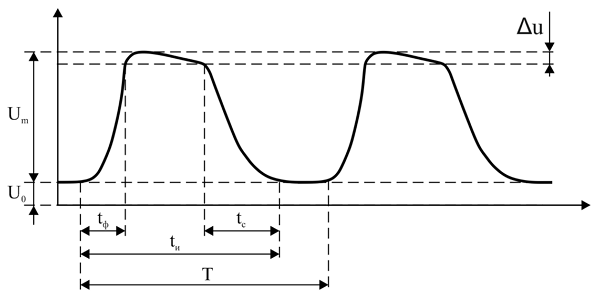
Форма реального импульса

Временные параметры импульса (t_и, t_ф, t_с, t_в) имеют точное значение только в случае идеального импульса, а в реальности лишь в некоторой степени имеют приближённое значение. Поэтому временные параметры отсчитываются от некоторых приближённых величин, которые в достаточной для практики точности имеют значения 0,05 и 0,95. Поясню на примере формы реального импульса, изображённого выше: при определении длительности фронта (t_ф) импульса, за начало фронта принимают значение 0,05*U_m, а за окончание фронта – 0,95*U_m. В случае длительности среза, соответственно, начало – 0,95*U_m, а окончание – 0,05*U_m.

Переходный процесс

Рассмотрение импульсных устройств и схем не возможно без представлении о переходном процессе. Он возникает в цепях при различных коммутациях, то есть при включении или выключении элементов схемы, источников напряжения, при коротких замыканиях отдельных цепей и т.д. Переходный процесс объясняется тем, что энергия электромагнитных полей, связанных с цепью, в разные промежутки времени неодинакова, а резкое изменение энергии невозможно из-за ограниченной мощности источников питания.

Исходя из вышесказанного, можно сделать вывод, что напряжение наёмкости и ток в индуктивность не могут изменяться скачкообразно, так как данные параметры определяют энергию электрического поля конденсатора и магнитного поля катушки индуктивности.

Таким образом, можно сделать вывод, что при рассмотрении импульсных схем наибольшее внимание необходимо обратить на цепи, представляющие собой комбинации резисторов и конденсаторов или резисторов и катушек индуктивностей (RC- и RL-цепей). Такие цепи применяются непосредственно для формирования импульсов, а также являются важнейшими элементами релаксационных генераторов, триггеров и других устройств. Поэтому ниже рассмотрим основные свойства элементарных RC- и RL-цепей, а также изменение формы импульсов при прохождении через эти цепи.