Виды аналоговой модуляции

Амплитудная модуляция (АМ) может быть определена как из­менение амплитуды несущей пропорционально уровню модулирующе­го сигнала (модуляция частоты и фазы в реальных устройствах при этом рассматривается только как паразитная). В случае гармоническо­го модулирующего колебания аналитическое выражение для АМ сиг­нала U(t) имеет вид

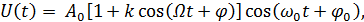(5.1)

где A₀,ω₀ = 2πf₀, 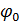- амплитуда, угловая частота и начальная фаза несущей соответственно; k = A_m/A₀ — коэффициент пропорциональности между модулирующим сигналом и вариациями амплитуды АМ колеба­ния или коэффициент модуляции; А_т Ω = 2πF φ— амплитуда, угловая частота и начальная фаза модулирующего колебания; t — время.

На рис. 5.2 приведен график АМ колебания в зависимости от вре­мени, на котором видно, что огибающая имеет форму гармонического модулирующего колебания.

Выражение (5.1) может быть преобразовано к виду (для простоты начальные фазы опущены)

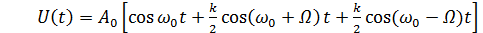(5.2)

Данная форма записи показывает, что в спектре модулированного ко­лебания кроме несущей, содержатся две боковые составляющие с ам­плитудой, пропорциональной коэффициенту модуляции и с частотами выше и ниже несущей на частоту модуляции Ω = 2πF (рис. 5.3). Ши­рина спектра такого АМ сигнала

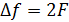(5.3)

Если низкочастотное модулирующее колебание является сложным, то спектр модулированного колебание будет содержать, кроме несущей, две боковые полосы — верхнюю и нижнюю. Они представляют собой перенесенный в область несущих частот спектр модулирующего сигнала без изменения и с инверсией соответственно. Для определения полной ширины спектра АМ колебания в этом случае в (5.3) подставляют максимальную частоту спектра модулирующего колебания.

Очень наглядна векторная диаграмма модулированного сигнала (рис. 5.4). Несущее гармоническое колебание отображается вектором

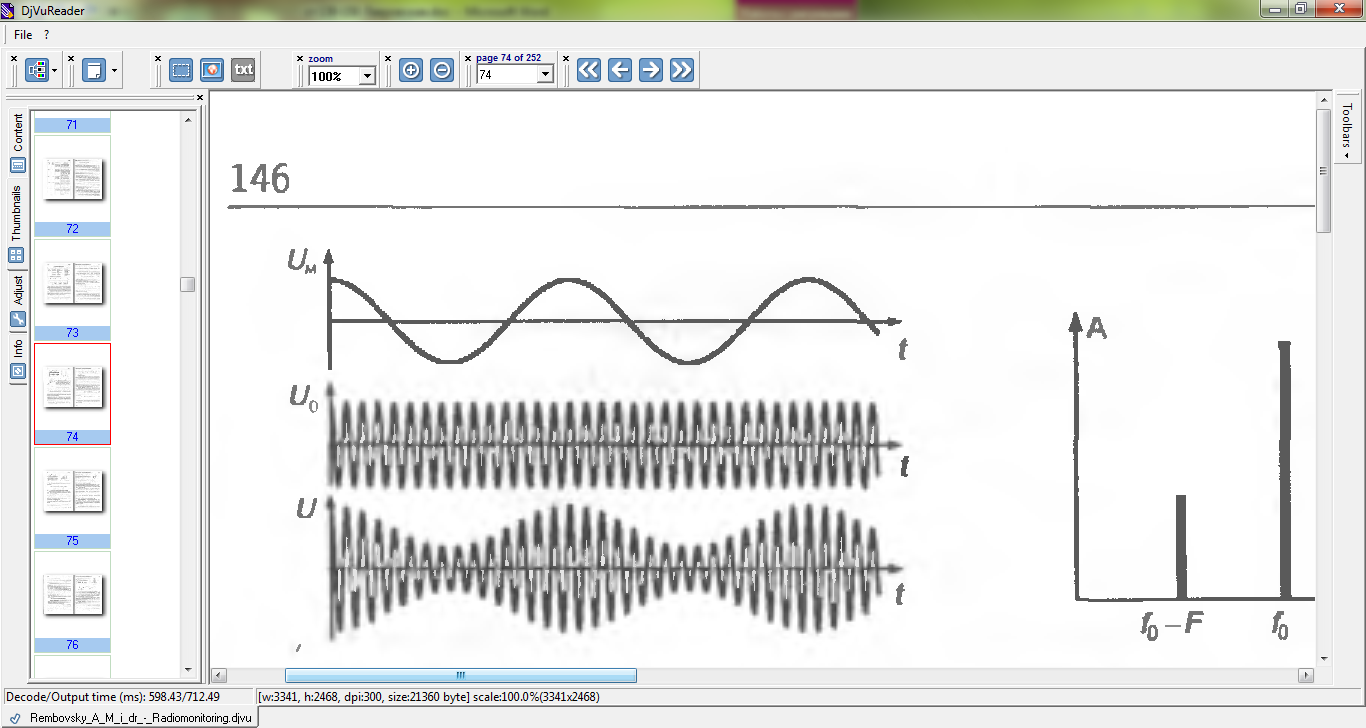
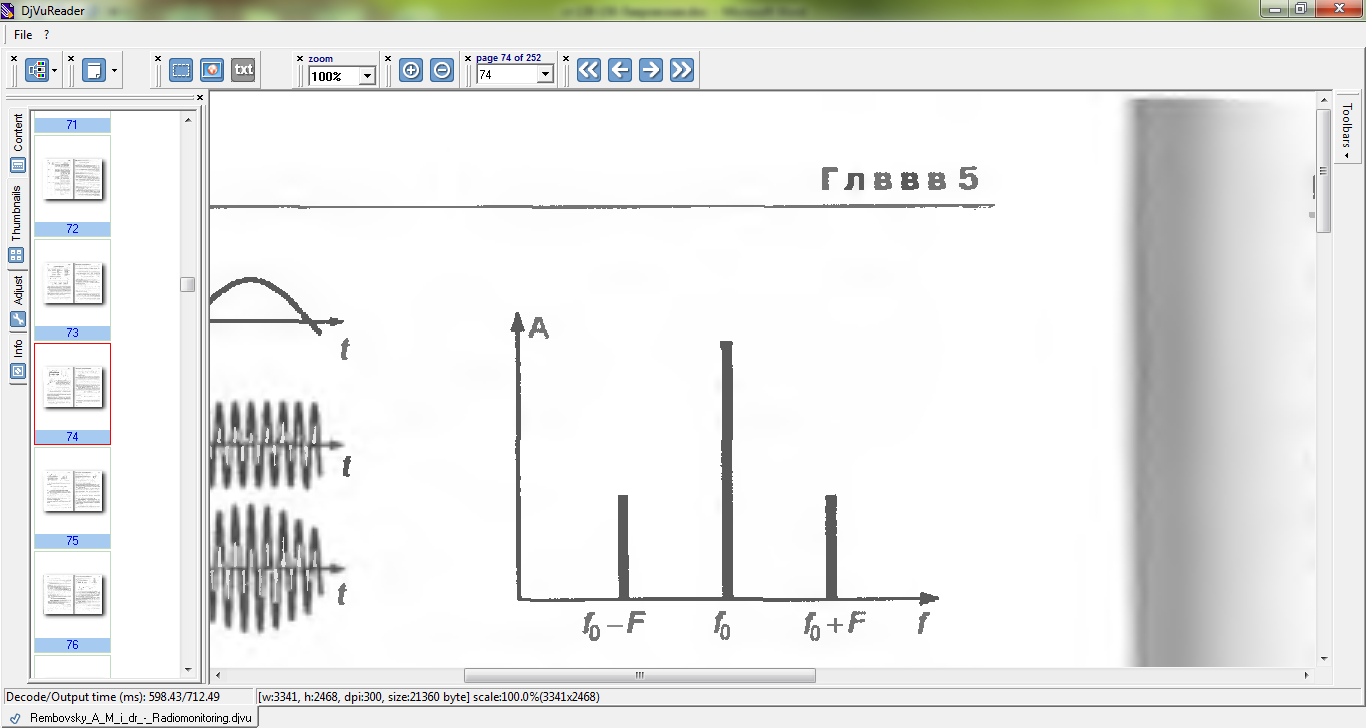
Рис. 5.2 График АМ колебания Рис.5.3 Спектр АМ колебания

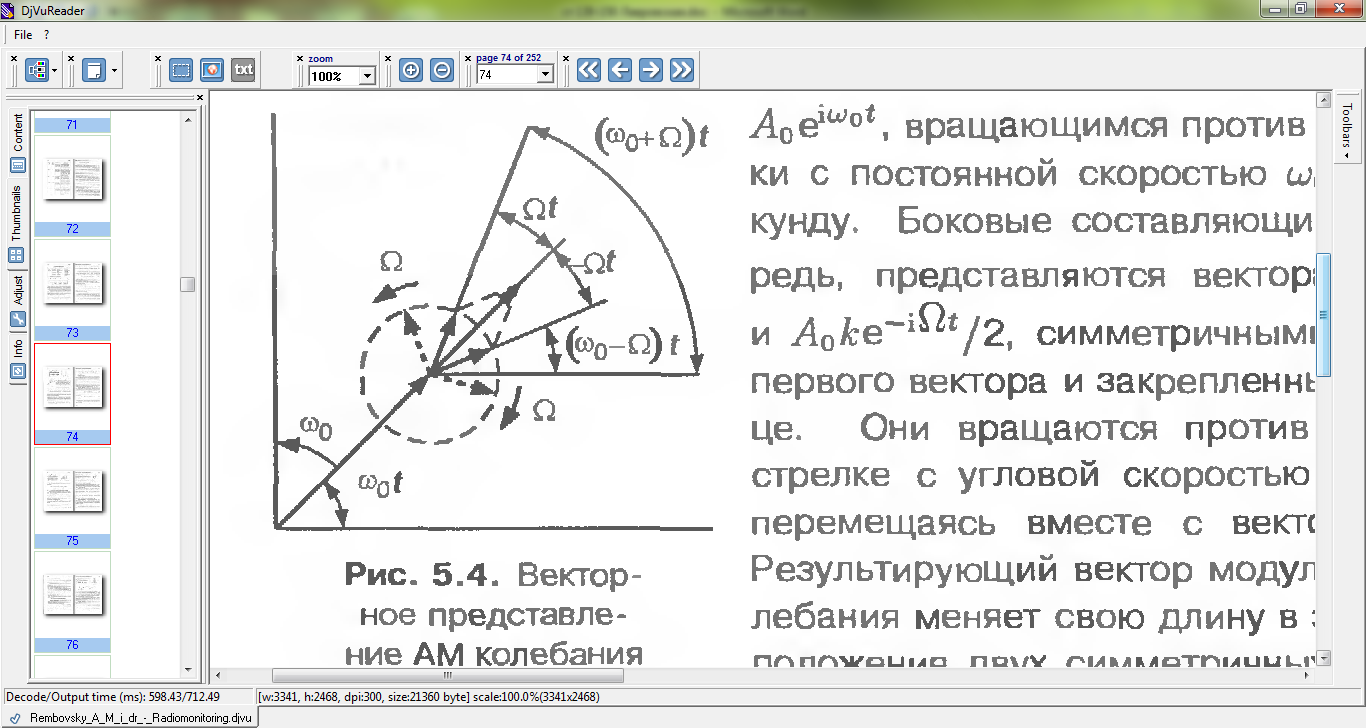
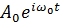, вращающимся против часовой стрелки с постоянной скоростью ω₀радиан в секунду. Боковые составляющие, в свою оче­редь, представляются векторам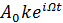и /2 и 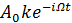/2, симметричными относительно первого векторе и закрепленными на его конце. Они

вращаются против и по часовой стрелке с угловой скоростью модуляции Ω, перемещаясь вместе с вектором несущей. Результирующий вектор модулированного колебания меняет свою длину в зависимости от положения двух симметричных векторов, ча­стота его вращения остается постоянной.

Мощность АМ колебания зависит от глубины модуляции. Мощность несущей частоты неизменна и пропорциональна 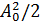. Мощность каждой боковой составляющей пропорциональна квадрату её амплитуды, то есть величине .

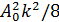При наиболее глубокой модуляции (k=1) мощность АМ колеба­ния (равная сумме мощностей всех трех составляющих) лишь в полтора раза превосходит мощность немодулированного колебания. На прак­тике среднее значение коэффициента амплитудной модуляции не превышает 0.5, чтобы уменьшить вероятность перемодуляции при пиковых значениях модулирующей функции.

С целью увеличении эффективности и использования передатчика и экономии полосы частот, занимаемой модулированным сигналом, передаваться может не весь спектр, а одна боковая полоса АМ колебания. При этом несущая и другая боковая подавляются. Такая модуляция называется АМ с одной боковой полосой (ОБП). Следует отметить, что в строгом смысле это уже будет колебание со сложной амплитудно-фазовой модуляцией.

Различают следующие разновидности амплитудной модуляции:

• двухполосная АМ (Double Sideband - DSB);

• двухполосная АМ с подавленной несущей (Double Sideband Supрrеssed Саrrier —DSBSC);

• однополосная АМ (Single Sideband);

• однополосная AM с подавленной несущей (Single Sideband Suppressed Carrier — SSBSC) в вариантах нижней и верхней боковой полосы (Lower Sideband – LSB и Upper Sideband - USB);

• АМ с частично подавленной одной из боковых полос (Vestigal Sideband - VSB);

• АМ с двумя независимыми боковыми полосами (Independend Single Sideband - ISSB).

Еще одним способом увеличения эффективности АМ является применение динамической АМ (ДАМ), при которой мощность несущей ре­гулируется в зависимости от амплитуды модулирующего колебания.

Амплитудная модуляция и ее разновидности нашли применение в основном в радио- и телевещании. В диапазонах ДВ и СВ применяется двухполосная АМ, в диапазоне КВ и УКВ — однополосная АМ. В диапа­зоне УКВ в системах ТВ для передачи сигнала изображения (яркостной составляющей) используется АМ с частично подавленной одной боко­вой полосой, а для передачи цветоразностных сигналов в системах РАL_ и NTSC используется разновидность балансной модуляции, так называемая квадратурная АМ. Принцип АМ ОБП используется для формирования групп каналов в многоканальных системах связи с частотным уплотнением. Кроме того, данный вид модуляции используется в си­стемах мобильной связи и для связи с самолетами (118...136 МГц).

Частотная модуляция (ЧМ) является частный случаем угловой мо­дуляции При ЧМ изменяемым параметром является частота несущей, т.е. в каждый момент времени ее отклонение от своего номинального значения пропорционально уровню модулирующего сигнала. В случае гармонического модулирующего колебания мгновенная частота

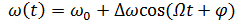, (5.4)

где 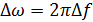— амплитуда отклонения несущей частоты от номи­нала или девиациz частоты.

Полная мгновенная фаза связана с его мгновенной частотой че­рез интеграл

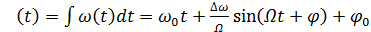(5.5)

Величина

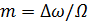(5.6)

называется индексом частотной модуляции. Для сложного модулирующего сигнала в (5.6) подставляется максимальная частота его спектра. Аналитическое выражение для ЧМ сигнала U(t) записывается сле­дующим образом:

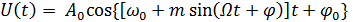, (5.7)

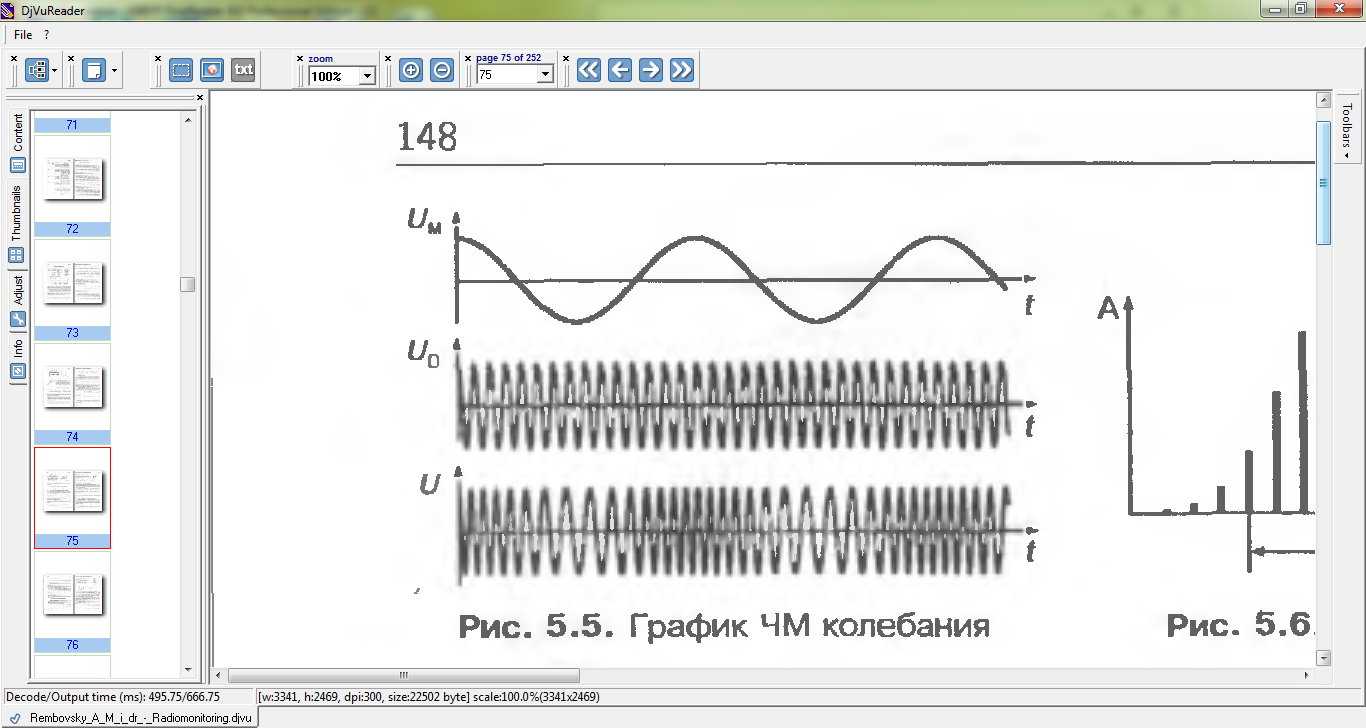
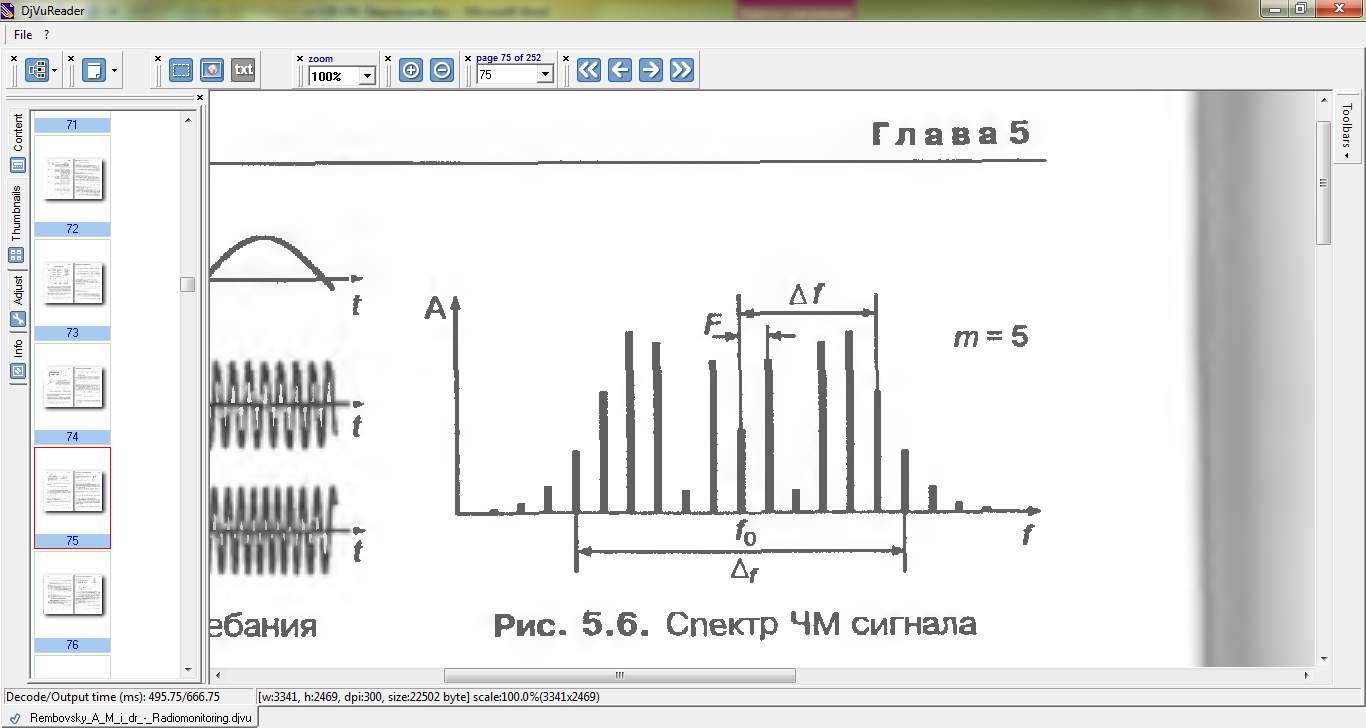
Рис. 5.5 График ЧМ колебания Рис. 5.6 Спектр ЧМ сигнала

График ЧМ сигнала представлен на рис. 5.5.

Спектр ЧМ колебания при однотональной модуляции можно полу­чить, представив колебание (5.7) в виде бесконечного тригонометри­ческого ряда

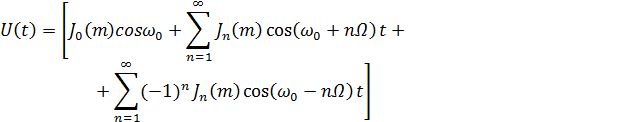
(5.8)

где 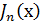— специальная функция Бесселя порядка n аргумента x.При фиксированное аргументе функция Бесселя с ростом поряд­ка убывает по абсолютной величине и при т > п имеет малую вели­чину. Поэтому на практике ограничиваются рассмотрением конечного числа составляющих спектра.

Вид спектра ЧМ колебания при модуляции гармоническим сигна­лом приведен на рис. 5.6.

Различают широкополосную т 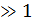( 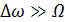) и узкополосную т 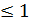( 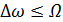) частотную модуляцию. В первом случае, как правило, учитывают составляющие с номерами n 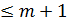. Это соответствует ши­рине спектра ЧМ колебания при гармонической модуляции в которой сосредоточено 99 % энергии сигнала.

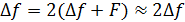(5.9)

При небольших индексах ЧМ (от 1 до 2.5) следует пользоваться

фор­мулой

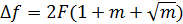(5.10)

За пределами этой полосы амплитуда составляющих в 100 раз меньше амплитуды немодулированной несущей

При т 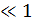ЧМ колебание (5.7) приближенно описывается как

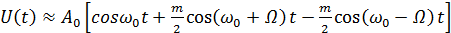(5 .11)

т.е. можно считать, что в спектре такого сиг­нала с частотной модуляцией присутствуют только несущая и две отстоящие от нее на частоту модуляции боковые компоненты. Од­нако в отличие от амплитудной модуляции вторая боковая составляющая имеет фазо­вый сдвиг на π радиан.

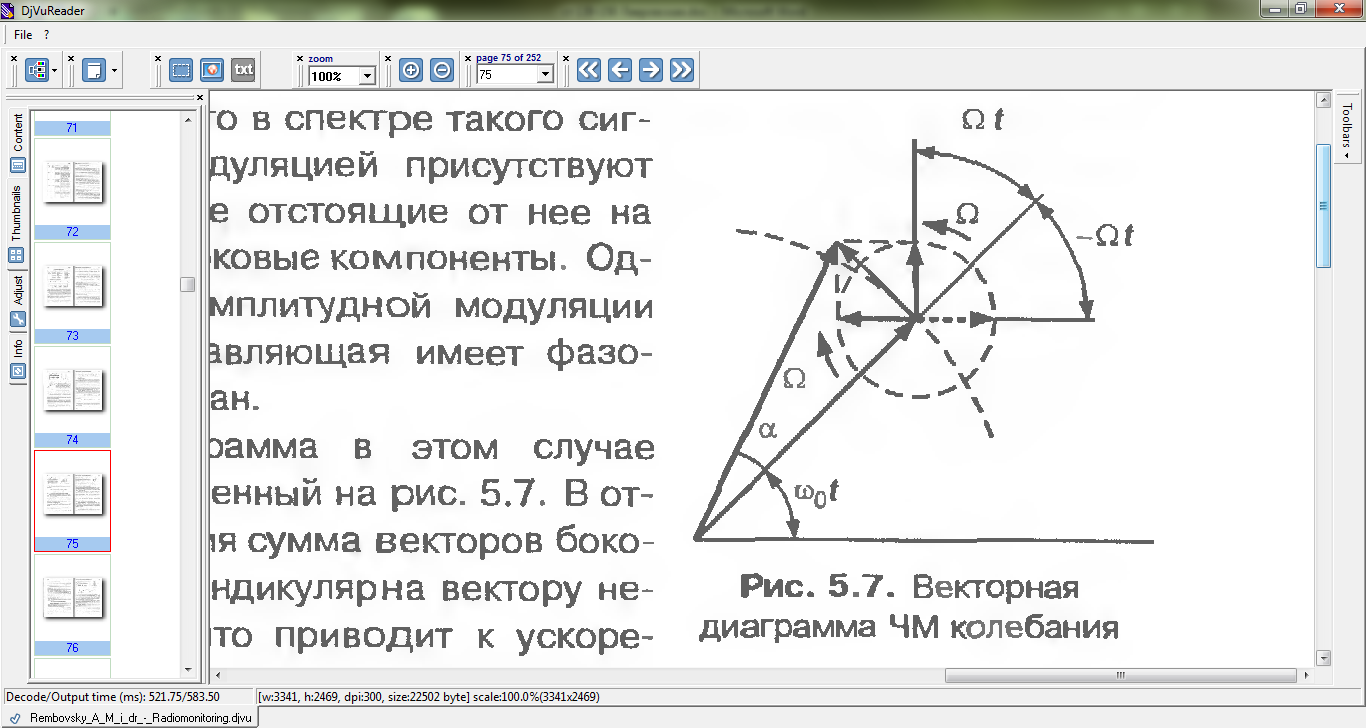
Векторная диаграмма в этом случае имеет вид, представленный на рис. 5.7. В от­личие от АМ колебания сумма векторов боковых колебаний перпендикулярна вектору несущего колебания, что приводит к ускоре­нию и замедлению вращения результирующего вектора. Длина этого вектора, представляющая амплитуду моду­лированного колебания, незначительно изменяется, что связано с допущенными приближениями. В общем случае будет складываться боль­шее число векторов, и конец результирующего вектора при его качании будет перемещаться по дуге окружности, т.е. длина результирующего векторе меняться не будет.

Поскольку спектр ЧМ сигнала шире, чем при АМ, помехоустойчивость такой модуляции выше. Применяется ЧМ по причине своей широкополосности в основном в диапазоне метровых и более коротких волн. Узкополосная ЧМ (Narrow Frequency Modulation - NFM) используется в системах мобильной связи, широкополосная (Wide Frequency Modulation — WFM) в радио- и телевещании. При стереофоническом вещании в модулирующем сигнале имеется поднесущая с дополнитель­ной модуляцией в зависимости от стандарта вещания. Кроме того ЧМ с 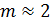широко применялась в системах радиорелейной и спут­никовой связи, модуляция несущей осуществлялась широкополосным групповым сигналом, но в настоящее время, такие сигналы практиче­ски вытеснены цифровыми.

В радиолокации ЧМ используется как внутриимпульсная в вариан­тах линейной ЧМ, симметричной, зигзагообразной и др.

Фазовая модуляция (ФМ) также является частным случаем угло­вой модуляции. Рассмотренное выше частотно-модулированное коле­бание является в то же время и фазомодулированным. Однако при фазовой модуляции изменение фазы, а не частоты, должно совпадать с законом изменения модулирующего колебания В случае синусои­дального модулирующего колебания аналитическое представление ФМ колебания имеет вид

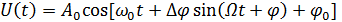(5.12)

где 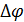– амплитуда отклонения (девиация) фазы.

Когда осуществляется угловая модуляция гармоническим сигна­лом, отличить частотную модуляцию от фазовой можно, только сравнив изменений мгновенной фазы модулированного колебания с законом из­менения модулирующего напряжения.

Сравнение (5.7) и (5.12) показывает, что индекс частотной модуляции ранен амплитуде отклонения фазы, измеряемой в радианах. Однако при частотной модулями индекс модуляции обратно пропорционален модулирующей частоте, а при фазовой девиация фазы фиксируется и от частоты модуляции не зависит.

Спектр фазомодулированного гармоническим колебанием сигнала будет такой же, как и частотно-модулированного, если одинаковы ин­дексы модуляции. При 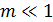спектр ФМ сигнала будет содержать несущую и две боковые составляющие, отстоящие от несущей на частоту модуляции. Отличие от спектра АМ сигнала заключается только в том, что боковые составляющие сдвинуты по фазе на 90°.

При больших индексах модуляции ширину спектра ФМ сигнала сле­дует рассчитывать, пользуясь формулами для ЧМ сигналов. Ширина спектра в том и другом случае определяется девиацией частоты. Но следует отметить, что с увеличением частоты модуляции у ЧМ сигнала ширина спектра будет оставаться прежней при меньшем числе спек­тральных составляющих, а при ФМ ширина спектра будет расти при неизменном числе этих составляющих.

Векторная диаграмма ФМ не отличается от векторной диаграммы ЧМ. Нужно лишь иметь в виду, что ФМ определяется угловым откло­нением результирующего вектора от положения вектора несущей ча­стоты, а ЧМ скоростью этого отклонения, т.е. производной фазы по времени. Фазовая модуляция применяется в основном в радионави­гационных системах.