Построение шкал измерений
В простейшем случае оценка измеряемого признака некоторым индивидом производится путем выбора, как правило, одного ответа из серии предложенных или путем выбора одного числового балла из некоторой совокупности чисел. Таким оценкам предшествует построение шкалы измерений.
Для оценки измеряемого качества иногда пользуются графическими шкалами, разделенными на равные части и снабженными словесными или числовыми обозначениями. Респондента просят сделать отметку на шкале в соответствии с его оценкой данного качества.
Ранжирование объектов является другим широко используемым приемом измерения. При ранжировании производится оценивание по измеряемому качеству совокупности объектов путем их упорядочивания по степени выраженности данного признака. Первое место, как правило, соответствует наиболее высокому уровню. Каждому объекту приписывается оценка, равная его месту в данном ранжированном ряду.
Возможно попарное сравнение исследуемой совокупности по измеряемому качеству и дальнейшее упорядочивание их на основе результатов сравнения. Однако данный подход является более сложным и его, скорее, применяют при опросах экспертов, а не массовых респондентов.
Так, при построении шкалы часто используются экспертные оценки, а в дальнейшем принятая шкала применяется при проведении полномасштабного исследования.
Рассмотрим измерение, направленное на построение шкалы, т.е. построение шкальных весов оцениваемых признаков. Для этого после определения числа и названий исследуемых признаков экспортно проводится назначение каждому признаку определенной количественной меры. Проще, но не лучше, осуществить построение шкалы с помощью простейших экспертных методов путем простого ранжирования или используя балльные шкалы. Полученные таким путем ранги (веса) оцениваемых признаков скорее всего будут носить ориентировочный характер. Причем многие эксперты, если не оговорить специальные правила определения шкальных весов, просто затруднятся провести такое измерение. Поэтому в данном случае целесообразно использовать более сложные методы.
При решении подобных задач часто используется метод парных сравнений. Предположим, что строится шкала для выяснения отношения к таким ценностям продукта, как «польза», «дизайн», «качество», «срок гарантии», «послепродажный сервис», «цена» и т. п. Предполагаем, что простое ранжирование (определение весов признаков) затруднено или имеет большое значение достаточно точное определение шкальных весов исследуемых признаков, поэтому прямое их экспертное определение не может быть осуществлено. Обозначим для простоты эти ценности символами А1, А2, А3,..., А k.
Сущность метода парных сравнений состоит в том, чтобы предложить экспертам произвести сравнение объектов попарно, с тем чтобы установить в каждой паре наиболее важный (значимый) из них.
Из символов образуем всевозможные пары: (А1А2), (А1А3) и т. д. Всего таких парных комбинаций получится k • (k — 1)/2, где k — количество оцениваемых признаков.
Выделенные пары признаков предъявляются экспертам на отдельных карточках так, чтобы одно и то же понятие не появлялось подряд в двух последовательно идущих карточках.
Результаты опроса сводятся в таблицу по образцу табл. 4.8, в которой приведены гипотетические результаты опроса 30 экспертов по 5 признакам.
Таблица
Определение шкальных весов на основе парного сравнения
Ценности А1 А2 А3 А4 А5
А1 — 0,82 0,89 0,95
А2 0,39 — 0,51 0,60 0,69
А3 0,18 0,49 — 0,68 0,73
А4 0,11 0,40 0,32 — 0,82
А5 0,05 0,31 0,27 0,08 —
Число на пересечении, например, первой строки (А1) и второго столбца (А2) представляет собой долю случаев предпочтения признака А2 признаку А1 (общее число суждений равно n, где n — число экспертов). Очевидно, что на пересечении второй строки и первого столбца должно стоять число, дополняющее предыдущую долю до единицы. Если эксперт затрудняется выбрать предпочтительный признак, то в таблицу заносится число 0,5.
В математической модели, лежащей в основе построения шкалы методом парных сравнений, предполагается, что доля случаев предпочтения признака i признаку j f (mij) подчиняется нормальному закону, т.е.
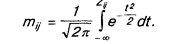
Следующий шаг в построении шкальных оценок заключается в том, чтобы обратить наблюдаемые отношения mij в Zij по приведенному уравнению. По приложению для каждого значения mij (из табл. 4.8) находят Zij и заносят в табл. 4.9.
В приложении приведены значения интеграла в пределах от 0 до Z, а не от— ∞ до Z, как требует того приведенная выше формула. Поэтому при использовании этой таблицы надо исходить из следующего: табл. 4.8 антисимметрична относительно диагонали (на диагонали стоят нули), т. е. Zij == Zij; причем значения Z положительны тогда, когда mij (табл. 4.8) больше 0,5. Поэтому берем из табл. 4.8 те mij, которые больше 0,5, вычисляем разности (mij — 0,5). По приложению для них находим Zij и записываем в табл. 4.9 со знаком «плюс». Симметричное к нему число Zij имеет знак «минус» и ту же абсолютную величину.
Если Zij оказывается большим, чем 2,0, или меньшим 2,0, оно отвергается как нестабильное. Если ни одна из оценок не отвергается, то шкальная оценка признака i будет равна средней величине всех чисел в графе i табл. 4.9. Когда некоторые j отвергаются, то в табл. 4.9 ставится прочерк. Далее из данных столбца 2 вычитаются данные столбца 1, из 3 — 2 и т. д., а результат заносится в новую таблицу. При этом разность между двумя прочерками или между значением и прочерком считается незначимой и в матрице ставится прочерк. Для преобразованной таблицы вновь вычисляются средние по столбцам, которые и отождествляются с весом признака измеряемого явления.
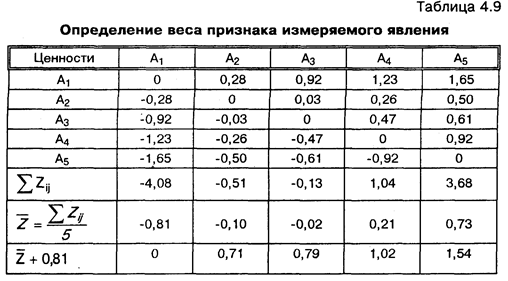
Нулевую точку устанавливают произвольным образом (см., например, последнюю строку в табл. 4.9).
Метод парных сравнений может использоваться также при определении относительных весов целей, критериев, факторов и др., осуществляемом при проведении различных маркетинговых исследований.
При большом числе признаков метод парных сравнений оказывается громоздким, поскольку эксперты должны рассмотреть каждую возможную пару признаков, а число таких пар быстро растет с ростом числа признаков. Так, при k = 5 число пар равно 10, при k = 30 — 435.
В таких случаях используются некоторые другие методы, из которых наибольшее применение получил метод равных интервалов [19].
Лайкерт в 1932 г. предложил метод измерения без использования экспертной оценки, который получил название шкалы Лайкерта (метод суммарных оценок). Группе лиц даются вопросы, которые должны оцениваться по пятибалльной системе в отношении согласия с этими вопросами (суждениями);
5 — «полностью согласен»
4 — «согласен»
3 — «нейтрален»
2 — «не согласен»
1 — «полностью не согласен».
Баллы одного лица относительно всех вопросов суммируются. Полученная сумма — балл этого лица. Затем лица ранжируются по баллам.
Для построения шкалы отбирается большое число вопросов, относящихся к исследуемой проблеме.
Данный метод можно использовать для отбора наиболее значимых вопросов для их включения в анкету, особенно в случае, когда имеется большое количество вопросов и реально существует проблема их отбора для включения в анкету.
Например, ограниченной группе потребителей или экспертов в 10 человек (А, Б, В и т.д.) дается 10 вопросов, из которых производится отбор. Вопросы оцениваются по пятибалльной шкале Лайкерта. Каждому лицу дается бланк (табл. 4.10).
Таблица 4.10. Иллюстрация метода суммарных оценок
| Номер вопроса | Ответ | ||||
| полностью согласен | согласен | нейтрален | не согласен | полностью не согласен | |
| 1-й | + | ||||
| 2-й | + | ||||
| 3-й | + | ||||
| 4-й | + | ||||
| 5-й | + |
Продолжение табл. 4.10
| Номер вопроса | Ответ | |||
| полностью согласен | согласен | нейтрален | не согласен | полностью не согласен |
| 6-й | + | |||
| 7-й | + | |||
| 8-й | + | |||
| 9-й | + | |||
| 10-й | + |
Индивид делает отметку по каждому вопросу в соответствии со своим отношением к нему. Далее подсчитывается общий балл лица относительно всех вопросов. Полученные данные сводятся в следующую таблицу (здесь даны вычисления для пятого вопроса).
| Лицо | Общий балл | Балл пятого вопроса | Разность | Лицо | Общий балл | Балл пятого вопроса | Разность |
| А | Е | ||||||
| Б | И | ||||||
| В | К | ||||||
| Г | Л | ||||||
| Д | М |
Затем строится таблица сопряженности между баллами вопроса и величинами в графе «разность», причем разности сгруппированы по интервалам (табл. 4.11).
Таблица 4.11. Таблица сопряженности
Балл Интервал разностей Балл Интервал разностей
10-19 20-29 30-39 40-50 10-19 10-29 30-39 40-50
— — — — —
— — — . — —
— — —
Вычисляется коэффициент корреляции между баллом и разностью. И так для каждого вопроса. Вопросы с малыми корреляциями выбрасываются.
Техника построения шкал методом суммарных оценок обеспечивает порядковый уровень измерения.
Проблема сопоставимости признаков, измеренных по разным шкалам, с одной стороны, и желание иметь некий интегральный показатель для характеристики совокупности свойств измеренного объекта — с другой, приводят к задаче объединения нескольких признаков, измеренных по разным шкалам, в один общий, итоговый показатель — индекс.
Следует помнить, что было бы большим заблуждением требовать от индекса того, чего он не может дать, — полной качественной характеристики объекта наблюдения, так как задача шкалирования предполагает .всего лишь разработку механизма сведения качественных признаков к количественным.
При построении индекса измеряемое качество следует искать в сочетании оценок по совокупности исходных признаков.
В общем виде измеряемое качество у можно представить некоторой функцией исходных признаков (х), т. е.
Y=f(Х1, Х2,..., Хk).
Возможны различные представления функции f и, с другой стороны, различные способы приписывания оценок исходным признакам {х}. В зависимости от этого можно выделить три существенно различных типа методов:
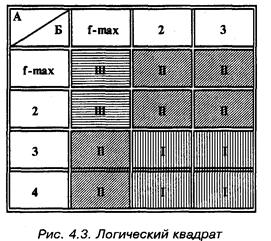
1. Конструкция индекса задана на основе предваряющих исследование логических операций. Так, приписывание респонденту значения по основному показателю может определяться некоторой логической схемой, например схемой логического квадрата.
Разберем этот случай на примере построения итогового индекса уровня индивидуальной свободы одеваться для подростка. Этот индекс может быть построен на базе двух исходных: в вопросе А подросток дает свою оценку предоставляемой ему родителями свободы выбора (оценки 1,2,3,4); вопрос Б содержит информацию о том, как родители, по мнению респондента, учитывают его индивидуальные склонности (оценки 1,2,3). Схема объединения вопросов А и Б в итоговом показателе дана на рис. 4.3. Итоговый индекс имеет три градации, различающиеся по уровню индивидуальной свободы, — 111,11,1.
2. Итоговый индекс может представлять собой аналитическую функцию от исходных признаков. Форма математической зависимости между исходными признаками обосновывается исходя из теоретических соображений.
Примером подобного рода косвенного измерения является шкала Лайкерта. Респонденту предъявляется серия из вопросов, связанных с исследуемым объектом либо непосредственно, либо только весьма косвенно. Общий балл респондента по всему вопроснику определяется как сумма его баллов x1 по всем признакам, т. е. суммарный балл равен x1 + x2 + x3+,..., +xk.
Другой пример касается определения устойчивости интересов респондента в проведении досуга с помощью индекса «стабильных занятий на досуге». Он представляет собой отношение количества «стабильных» занятий (z) к числу всех занятий (t), присутствующих в досуге респондента, т. е. индекс стабильности занятий имеет вид у == z/t.
3. Конструкция индекса может определяться путем применения некоторых формальных методов преобразования исходных признаков изучаемой совокупности. Обоснованность конструкции индекса и его формирование определяются непосредственно самим методом.
Наибольшую известность получили методы факторного анализа, распознавание образов, некоторые процедуры анализа причинных структур.
Во многих случаях при составлении вопросников нецелесообразно с «нуля» разрабатывать шкалы измерений. Лучше воспользоваться стандартными типами шкал, используемыми в области маркетинговых исследований. К числу таких шкал относятся: модифицированная шкала Лайкерта, шкала для изучения жизненного стиля и семантическая дифференциальная шкала.
На основе модифицированной шкалы Лайкерта (интервальная шкала), адаптированной под цели проводимого маркетингового исследования, изучается степень согласия или несогласия респондентов с определенными высказываниями. Данная шкала носит симметричный характер (табл. 4.12) и измеряет интенсивность чувств респондентов.
Таблица 4.12. Вопросник для выявления мнения потребителя относительно товара определенной марки
| Заявление | ||||||
| Сильно согласен | В какой-то мере согласен | Отношусь нейтрально | В какой-то мере не согласен | Сильно не согласен | ||
| 1. Джинсы (указывается конкретная марка) хорошо выглядят | ||||||
| 2. Данные джинсы имеют разумную цену | ||||||
| 3. Следующая пара ваших джинсов будет данной марки | ||||||
| 4. Данные джинсы легкоузнаваемые | ||||||
| 5. В данных джинсах вы чувствуете себя хорошо |
Существуют различные варианты модификации шкалы Лайкерта, например, вводится различное число градаций (7—9).
Школа для изучения жизненного стиля является специальным направлением применения модифицированной шкалы Лайкерта и предназначена для изучения системы ценностей, личностных качеств, интересов, мнений относительно работы, отдыха, покупок различных людей. Такая информация дозволяет принимать эффективные маркетинговые решения. Пример анкеты для изучения жизненного стиля приводится в табл. 4.13.
Таблица 4.13. Анкета для изучения жизненного стиля
Пожалуйста, обведите цифру, в наибольшей мере соответствующую степени Вашего согласия или несогласия с каждым утверждением.
| Утверждение | Сильно согласен | Согласен | И согласен и не согласен | Не согласен | Сильно не согласен |
| 1. Я покупаю много | |||||
| специальных товаров | |||||
| 2. Я обычно имею один и более видов одежды самой последней моды | |||||
| 3. Самое главное для меня — это мои дети | |||||
| 4. Я обычно содержу мой дом в большом порядке |
Продолжение табл. 4.13
| Утверждение | Сильно согласен | Согласен | И согласен и не согласен | Не согласен | Сильно не согласен |
| 5. Я предпочитаю провести вечер дома, чем пойти на вечеринку | |||||
| 6. Я люблю наблюдать или слушать трансляции футбольных матчей | |||||
| 7. Я зачастую оказываю влияние на покупки друзей | |||||
| 8. В следующем году я буду иметь больше денег на покупки |
Семантическая дифференциальная шкала содержит серию двухполярных определений, характеризующих различные свойства изучаемого объекта. Так как многие маркетинговые стимулы основаны на мыслительных ассоциациях и отношениях, не выраженных явно, то данный тип шкалы часто используется при определении имиджа товарной марки, магазина и т.п. Результаты изучения мнений потребителей относительно двух ресторанов (№1 и №2) на основе семантической дифференциальной шкалы приводятся в табл. 4.14.
Таблица 4.14. Сравнительная оценка двух ресторанов
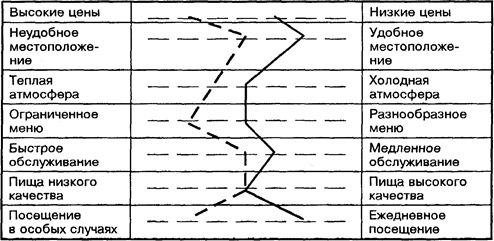
 - обозначения: - оценки ресторана №1,
- обозначения: - оценки ресторана №1,
 - оценки ресторана №2.
- оценки ресторана №2.
В табл. 4.14 специально положительные или отрицательные оценки не расположены только с одной стороны, а случайным образом перемешаны. Это сделано для того, чтобы избежать «гало эффекта». Он заключается в том, что если первый оцениваемый объект обладает более высокими оценками (которые расположены только с левой стороны анкеты) по сравнению со вторым объектом, то респондент будет иметь тенденцию и дальше ставить оценки слева.
Одним из достоинств данного метода является то, что если отдельным градациям в шкале присвоить номера: 1, 2, 3, и т.д. и ввести в компьютер данные разных респондентов, то конечные результаты могут быть получены в графическом виде (табл. 4.14).
При применении вышеназванных шкал возникает вопрос о целесообразности использования нейтральной точки. Все зависит от того, имеют или нет респонденты нейтральное мнение. Однозначной рекомендации по этому вопросу дать не представляется возможным.
То же самое можно сказать и относительно того, строить шкалу симметричной или несимметричной.
Существует великое множество вариантов шкал, построенных на основе изложенных принципов. Окончательный выбор обычно делается на основе испытания уровня надежности и точности измерений, проведенных с помощью различных вариантов шкал.
Дата добавления: 2021-04-21; просмотров: 662;











