Синтез последовательного корректирующего устройства

Основными требованиями работоспособности систем автоматического управления являются ее устойчивость и обеспечение требуемых показателей качества переходного процесса. К ним относятся: величина перерегулирования, статическая и динамическая ошибки, время регулирования, число колебаний. Устойчивость системы и показатели качества переходного процесса зависят от соотношения постоянных времени динамических звеньев, составляющих систему управления, и их передаточных коэффициентов. Постоянные времени и передаточные коэффициенты двигателя, УВП, датчиков определяются конструктивными параметрами и не могут быть изменены. Поэтому, если динамические свойства системы не отвечают предъявленным к ним требованиям, необходимо изменить структурную схему системы путем ввода корректирующих устройств (КУ). В зависимости от схемы их включения различают последовательные и параллельные корректирующие устройства. Структуру, параметры и место присоединений КУ определяют так, чтобы переходный процесс, вызванный соответствующим воздействием, протекал
в наименьшее время с наименьшим перерегулированием и числом колебаний не более трех.

Задача синтеза КУ заключается в определении его структуры и параметров по заданным показателям качества процессов регулирования. Для решения этой задачи и выяснения вопроса об устойчивости используют корневые и частотные критерии. В инженерной практике получил широкое распространение метод с применением логарифмических амплитудно-частотных и фазово-частотных характеристик (ЛАЧХ и ЛФЧХ), которые достаточно подробно рассмотрены в курсе ТАУ. Этот метод позволяет установить характер влияния каждого из звеньев на поведение системы, определить характеристику, параметры КУ, обеспечивающего требуемые показатели качества системы.

Рассмотрим основные положения синтеза [1, 11] последовательного КУ, включаемого непосредственно в цепь прохождения основного сигнала последовательно с основными звеньями, по заданным показателям перерегулирования s и времени переходного процесса t 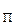(данные табл. П 1.1) с использованием ЛАЧХ и ЛФЧХ.

Желаемая ПФ разомкнутой системы с последовательным КУ:

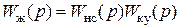, (4.54)

где W 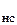(p) – ПФ по управлению нескорректированной системы; W 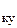(p) – ПФ корректирующего устройства.

ЛАЧХ КУ находится на основании желаемой ЛАЧХ, построенной по
заданным показателям качества регулирования s и t_п. Заменяя в (4.54)оператор Лапласа p на jw и логарифмируя, получим

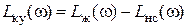, (4.55)

Таким образом, ЛАЧХ КУ равна разности желаемой ЛАЧХ и ЛАЧХ
не­скорректированной системы.

Порядок синтеза следующий:

Структурная схема замкнутой СУЭП преобразуется таким образом, чтобы после преобразования получилась единичная обратная связь.

Единичная обратная связь размыкается и строится ЛАЧХ и ЛФЧХ нескорректированной разомкнутой системы по участкам динамических звеньев, из которых состоит система электропривода.

Строится желаемая ЛАЧХ L_ж(w) для областей низких, средних и высоких частот (рис. 4.7).

Построение L_ж(w) начинают со среднечастотной асимптоты, предварительно определив частоту среза w_с по заданным величинам s и t_п. С достаточной точностью определяют значение частоты среза:

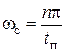, (4.56)

где n – коэффициент, определяемый графически.

Рис. 4.7. Логарифмические характеристики систем

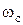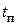Связь между и , устанавливаемая выражением (4.56), определяется по номограммам В. В. Солодовникова (рис. 4.8). Вначале по заданному значению sпо кривой 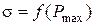определяется значение максимума вещественной частотной характеристики 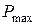. Далее по кривой 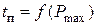по найденному 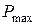определяют время регулирования 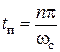и значение n в выражении (4.56).

Через полученную 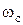проводится среднечастотная асимптота с наклоном 20 дБ/дек. Границы среднечастотной части желаемой ЛАЧХ выбирают исходя из условий обеспечения необходимого запаса устойчивости по модулю DL и фазе 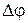. Ширину зоны средних частот находят по граничным частотам w₁ и w₂, которые определяются величиной требуемого запаса по амплитуде DL 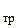и соответствующего запаса по фазе .

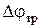Указанные значения 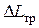и 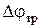получают на основе заданного значения 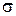по графикам (рис. 4.8, б).

Строятся низко- и высокочастотные асимптоты таким образом, чтобы они в возможно большем диапазоне совпадали с ЛАЧХ нескорректированной системы L_нс(условие наиболее простой реализации корректирующего звена).
В статической СУЭП низкочастотная асимптота L_жпредставляет собой горизонтальную прямую, находящуюся на расстоянии 201gK от оси абсцисс, где
K – коэффициент усиления разомкнутой системы. За высокочастотную асимптоту L_жпринимается линия, совпадающая с высокочастотной асимптотой ЛАЧХ разомкнутой системы или параллельная ей.

Рис. 4.8. Номограммы В. В. Солодовникова

Сопряжение низкочастотной и среднечастотной асимптот желаемой ЛАЧХ производится отрезками, имеющими наклон –20, –40, –60 дБ/дек, с таким расчетом, чтобы он отличался от наклона ЛАЧХ нескорректированной системы в том же диапазоне частот не более чем на 20 дБ/дек или совпадал
с наклоном L_нс.

Желательно, чтобы число изломов L_ж было минимально и их частоты L_жсовпадали с частотами L_нс. Соблюдение приведенных рекомендаций позволит упростить структуру КУ.

Графическим вычитанием ординат L_нс(w) нескорректированной системы из ординат желаемой L_ж(w) в соответствии с выражением (4.55)определяют ЛАЧХ корректирующего устройства (КУ).

По полученной ЛАЧХ КУ L_к(w) находят его передаточную функцию.