Основное уравнение центробежных машин

Частицы жидкости в каналах рабочего колеса совершают сложное движение – они перемещаются вдоль лопаток и одновременно вращаются вместе с колесом. Соответственно различают:

1. окружную скорость вращения частиц,

,

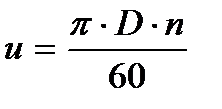(1)

где D – диаметр окружности вращения частицы;

n – число оборотов колеса в минуту.

2. относительную скорость ω перемещения частицы по отношению к лопатке.

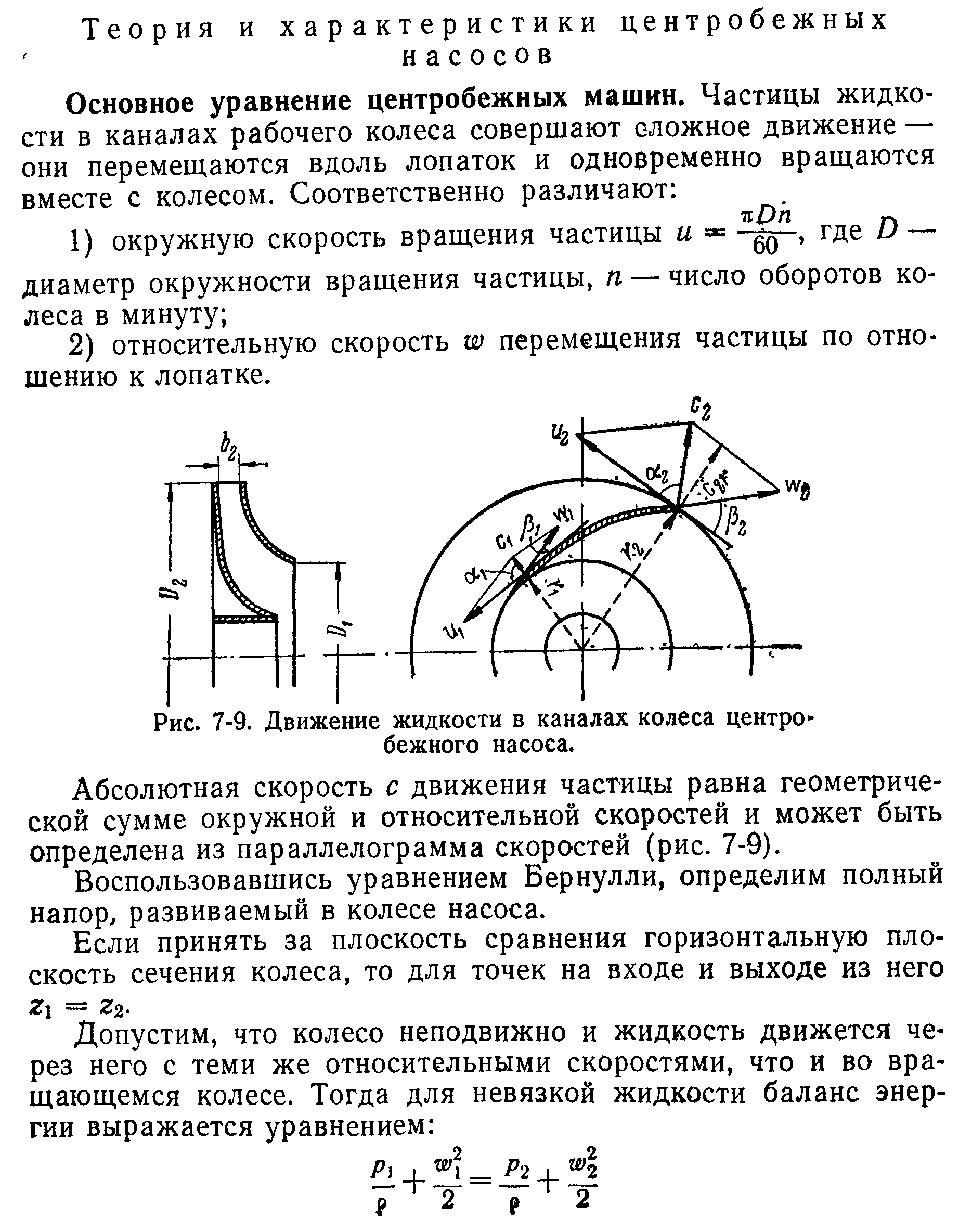
Рисунок 1 – Движение жидкости в каналах колеса центробежного насоса

Абсолютная скорость с движения частицы равна геометрической сумме окружной и относительной скоростей и может быть определена из параллелограмма скоростей (рис. 1).

Воспользовавшись уравнением Бернулли, определим полный напор, развиваемый в колесе насоса.

Если принять за плоскость сравнения горизонтальную плоскость сечения колеса, то для точек на входе и выходе из него .

Допустим, что колесо неподвижно и жидкость движется через него с теми же относительными скоростями, что и во вращающемся колесе. Тогда для невязкой жидкости баланс энергии выражается уравнением:

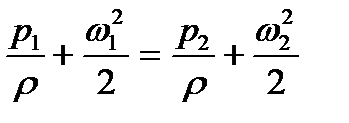
(2)

Во вращающемся колесе за счет работы центробежной силы жидкости сообщается дополнительная энергия А, и уравнение энергетического баланса приобретает вид:

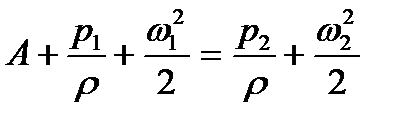
(3)

Энергия, сообщаемая центробежной силой 1 кг жидкости

,

(4)

где ω – угловая скорость колеса;

r₁ и r ₂ – радиусы вращения.

Учитывая, что 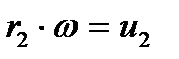и , получим:

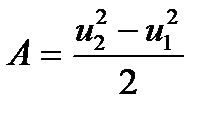
(5)

Вводя найденное значение А в левую часть уравнения (4), получим:

(6)

откуда

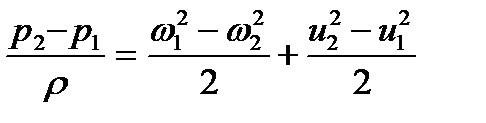
(7)

Согласно уравнению Бернулли, напор жидкости на входе в колесо и на выходе из него при 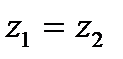составит:

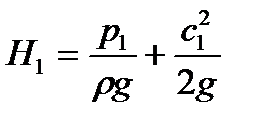
(8)

и

(9)

Откуда теоретический напор, развиваемый лопатками колеса, равен:

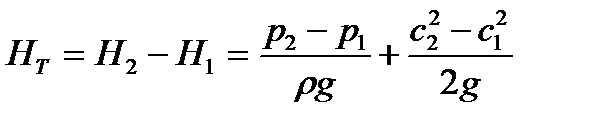
(10)

Подставив значение из выражения (7), получим:

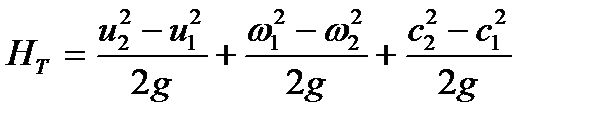
(11)

Примем, что жидкость движется через колесо с бесконечно большим числом лопаток, т. е. все частицы движутся по подобным траекториям. Тогда, согласно рис. 1, зависимость между скоростями частицы на входе в колесо и на выходе из него определится соотношениями:

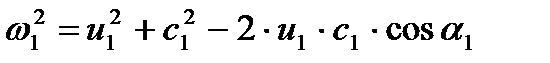
(12)

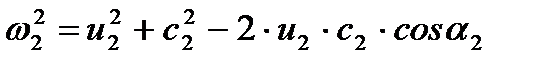
(13)

Вычитая из одного равенства другое, получим:

(14)

Подставив в выражение (11) и произведя сокращения, находим окончательное выражение теоретического напора:

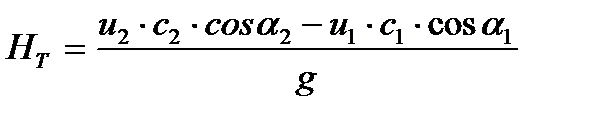
(15)

Уравнение (15), называемое основным уравнением центробежного насоса, было впервые выведено Л. Эйлером. Оно применимо ко всем центробежным машинам, в том числе к турбокомпрессорам, турбогазодувкам и вентиляторам.

Обычно жидкость поступает на лопатку колеса в радиальном направлении, под углом 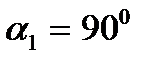. Следовательно, 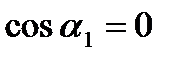и выражение (15) упрощается:

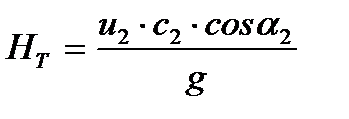
(16)

Из параллелограмма скоростей на выходе из колеса (рис. 1) видно, что 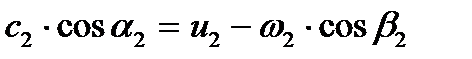, откуда

(17)

Фактический напор меньше теоретического, так как часть его теряется на преодоление гидравлических сопротивлений внутри насоса, а траектории частиц жидкости при конечном числе лопаток неодинаковы. Поэтому фактический напор насоса равен:

,

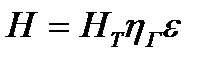(18)

где 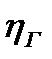- гидравлический к.п.д., равный 0,8 - 0,95;

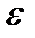- поправочный коэффициент, учитывающий понижение напора при конечном числе лопаток ( величина ).

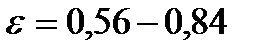Из выражения (15) и (17) следует: чем меньше угол и больше угол , тем больше напор. При и теоретический напор имеет наибольшую величину. Однако с увеличение угла 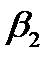значительно возрастают гидравлические потери. Поэтому центробежные насосы изготовляют с загнутыми назад лопатками ( ).

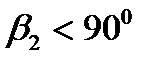Если лопатки загнуты вперед, то 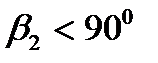, имеет положительное значение и

(19)

Если лопатки загнуты назад, то будет иметь отрицательное значение и

(20)

Наконец, если лопатки расположены радиально, то 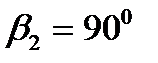, и

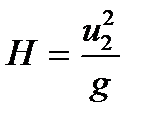
(21)

Таким образом, теоретически наибольший напор может быть достигнут, если лопатки загнуты вперед, и наименьший – если загнуты назад.

Производительность насоса, соответствующая расходу жидкости на выходе из колеса при ширине его b₂ (рис. 1), составляет:

,

(22)

где 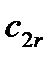- радиальная составляющая абсолютной скорости.

Высота всасывания

Всасывание жидкости насосом происходит под действием разности внешнего давления р₀ в приёмном резервуаре и давления р₁ на входе в насос или разности напоров 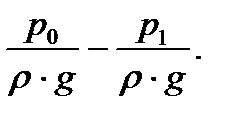Согласно уравнению Бернулли, разность напоров 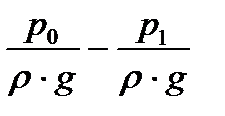затрачивается на подъём жидкости на высоту всасывания (см. рис. 2,а), на движение жидкости со скоростью 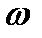, т.е. создание скоростного напора , и на преодоление гидравлических потерь во всасывающей трубе. Если жидкость засасывается из открытого бака, то внешнее давление равно атмосферному и можно записать равенство:

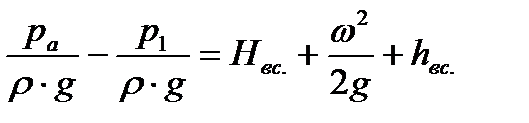
(13)

Чтобы происходило всасывание, давление р₁ должно быть больше давления р_t насыщенных паров жидкости при данной температуре. Тогда с учётом приведённого выше равенства условие нормальной работы насоса выразится следующим образом:

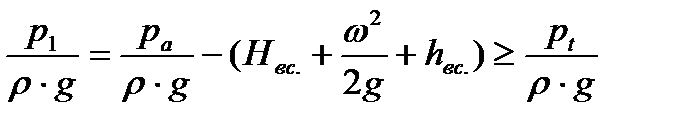
(14)

откуда

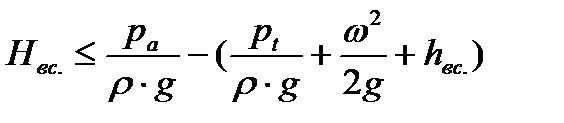
(15)

Из выражения (15) следует, что высота всасывания насоса уменьшается со снижением барометрического давления р_а и с увеличением давления паров р_t. Величина р_t возрастает с повышением температуры, поэтому при повышении температуры жидкости допустимая высота всасывания уменьшается. Когда давление р₁ становится равным р_t, из жидкости начинают интенсивно выделяться пары и растворённые в ней газы. При этом под действием противодавления р_t паров и газов высота всасывания снижается и может достигнуть нуля.

Высота всасывания уменьшается также при увеличении скорости жидкости во всасывающей трубе и соответствующем возрастании потерь h_вс. Обычно высота всасывания при перекачивании холодных жидкостей не превышает 5-6 м; при перемещении нагретых жидкостей она может быть значительно меньше. Поэтому горячие, а также вязкие жидкости подводят к насосу под некоторым избыточным давлением или с подпором на стороне всасывания (рис. 2,б). Зависимость (15) является общей для всех насосов, хотя процессы всасывания и нагнетания существенно отличаются для насосов различных типов.

Кавитация

В случае местных падений давления в насосе ниже давления насыщенного пара жидкости при данной температуре из жидкости начинают выделяться пары и растворенные в ней газы. Пузырьки пара, увлекаемые жидкостью по каналам колеса в область более высоких давлений, быстро конденсируются. Жидкость мгновенно проникает в пустоты, образующиеся при конденсации пузырьков, что приводит к многочисленным мелким гидравлическим ударам, сопровождающимся шумом и сотрясениями насоса. Производительность, напор и к. п. д. насоса при этом резко падают. Описанное явление носит название кавитации и приводит к быстрому механическому и химическому (от действия выделяющихся газов) разрушению насоса.

Чтобы избежать кавитации, повышают давление жидкости на входе в насос, уменьшая высоту всасывания или работая с подпором. Кроме того, для повышения стойкости к кавитации колеса насосов изготовляют из высокопрочных материалов.