Задачи нечеткой классификации
Пусть имеется набор 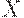 фотографических портретов всех членов нескольких семей. Требуется разделить этот набор на группы так, чтобы в каждой оказались портреты членов только одной семьи. Пусть
фотографических портретов всех членов нескольких семей. Требуется разделить этот набор на группы так, чтобы в каждой оказались портреты членов только одной семьи. Пусть 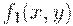 — функция принадлежности нечеткого бинарного отношения сходства на заданном наборе фотографий. Для каждой пары фотографий
— функция принадлежности нечеткого бинарного отношения сходства на заданном наборе фотографий. Для каждой пары фотографий 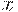 и
и 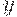 значение
значение 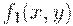 есть субъективная оценка человеком степени сходства
есть субъективная оценка человеком степени сходства 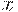 и
и 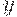 . Это нечеткое отношение можно рассматривать как своего рода "экспериментальные данные", отражающие понимание человеком понятия "сходства" в данной задаче. Следующий этап — использование этих "данных" для требующейся классификации фотографий.
. Это нечеткое отношение можно рассматривать как своего рода "экспериментальные данные", отражающие понимание человеком понятия "сходства" в данной задаче. Следующий этап — использование этих "данных" для требующейся классификации фотографий.
Заметим, что нечеткое отношение 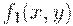 обладает естественными свойствами рефлексивности и симметричности. Оно называется одношаговым отношением, в том смысле, что описывает результаты лишь попарного сравнения портретов друг с другом. Для
обладает естественными свойствами рефлексивности и симметричности. Оно называется одношаговым отношением, в том смысле, что описывает результаты лишь попарного сравнения портретов друг с другом. Для 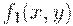 вводится
вводится 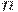 -шаговое отношение
-шаговое отношение 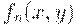 следующим образом:
следующим образом:
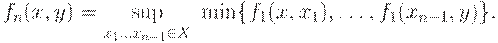
Это отношение является 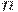 -арной композицией исходного "экспериментального" отношения
-арной композицией исходного "экспериментального" отношения 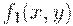 и представляет собой в некотором смысле его уточнение. Нетрудно показать, что для любых
и представляет собой в некотором смысле его уточнение. Нетрудно показать, что для любых 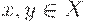 выполняется цепочка неравенств
выполняется цепочка неравенств
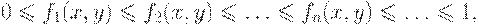
из которой следует, в частности, что для любых 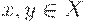 последовательность
последовательность 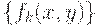 имеет предел при
имеет предел при 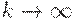 . Таким образом, существует предельное отношение сходства, определяемое равенством
. Таким образом, существует предельное отношение сходства, определяемое равенством
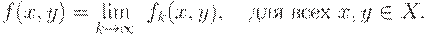
Это предельное отношение является конечным результатом обработки результатов нечетких измерений 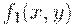 и следующим образом используется для классификации.
и следующим образом используется для классификации.
Для произвольного числа 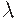 (
( 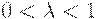 ) вводится обычное (не нечеткое) отношение
) вводится обычное (не нечеткое) отношение 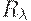 :
:
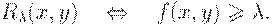
Нетрудно показать, что для любого 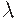 (
( 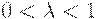 )
) 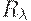 есть отношение эквивалентности в
есть отношение эквивалентности в 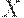 , т.е. для любых
, т.е. для любых 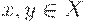 выполняются обычные аксиомы эквивалентности
выполняются обычные аксиомы эквивалентности
(1) 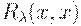 — рефлексивность,
— рефлексивность,
(2) 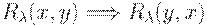 — симметричность,
— симметричность,
(3) 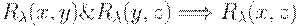 — транзитивность.
— транзитивность.
Заметим, что (3) есть следствие того, что предельное нечеткое отношение 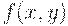 обладает свойством нечеткой транзитивности
обладает свойством нечеткой транзитивности
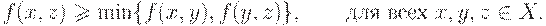
Окончательный этап алгоритма классификации — разбиение множества 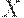 на классы эквивалентности по полученному отношению
на классы эквивалентности по полученному отношению 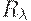 .
.
Выбор величины порога 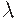 в этом алгоритме осуществляется, исходя из условий начальной задачи. В приведенном выше примере с фотографиями этот выбор осуществляли следующим образом. Пусть имеется набор из 20 фотографий представителей 3 семей. Тогда величину
в этом алгоритме осуществляется, исходя из условий начальной задачи. В приведенном выше примере с фотографиями этот выбор осуществляли следующим образом. Пусть имеется набор из 20 фотографий представителей 3 семей. Тогда величину 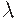 выбирают так, чтобы в результате реализации алгоритма классификации получилось 3 класса эквивалентности по отношению
выбирают так, чтобы в результате реализации алгоритма классификации получилось 3 класса эквивалентности по отношению 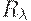 .
.
Дата добавления: 2016-12-27; просмотров: 1846;











