Задачи нечеткого упорядочения

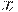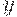Любую задачу принятия решений можно сформулировать как задачу отыскания максимального элемента в множестве альтернатив с заданным в нем отношением предпочтения. Однако во многих реальных ситуациях в множестве альтернатив можно определить лишь нечеткое отношение предпочтения, т.е. указать для каждой пары альтернатив и лишь степени, с которыми выполняются предпочтения 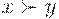и 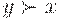. В таких случаях задача принятия решения становится неопределенной, поскольку неясно, что такое максимальный элемент для нечеткого отношения предпочтения. Для двух типов нечетких отношенийможно предложить способы упорядочения элементов конечного множества, в котором задано нечеткое отношение. Способы эти сводятся к тому, что для каждого из рассматриваемых типов нечетких отношений строится некоторая функция (напоминающая функцию полезности), и элементы множества упорядочиваются по соответствующим им значениям этой функции.

Пусть 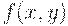— функция принадлежности бинарного нечеткого отношения в множестве 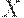(например, отношения нестрого предпочтения). Допустим, что рассматривается задача упорядочения элементов конечного множества . Упорядочение можно осуществлять по значениям следующей функции:

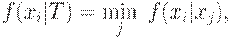
где 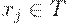, а функция

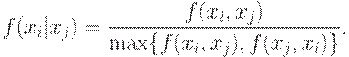
Для вычисления значений функции удобно пользоваться следующим равенством:

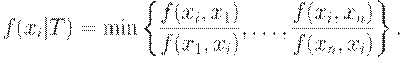
По отношению к этому упорядочению максимальным в множестве 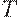является элемент 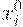такой, что

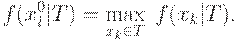
Рассмотрим еще одну задачу упорядочения, иллюстрируемую следующим примером.

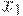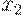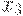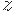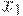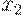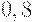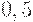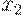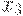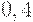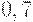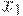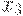Требуется решить, кто из детей: старший сын , младший сын или дочь больше всего похож на отца . Заданы "результаты измерений": и взятые отдельно, похожи на отца со степенями и соответственно; и , взятые отдельно, похожи на отца со степенями и ; наконец, и , взятые отдельно, похожи на отца со степеням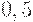и и .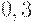

Таким образом, в этой задаче, в отличие от предыдущей, имеется стандартный элемент (шаблон) для упорядочиваемогомножества 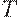, т.е. элемент, обладающий свойствами, общими для всех элементов этого множества. Иначе говоря, если 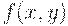— нечеткое отношение в 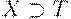(например, отношение сходства), то

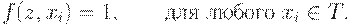
При наличии стандартного элемента для каждой пары элементов 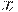и 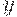множества 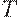задаются величины 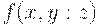, , 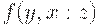т.е. степени отношения (например, сходства) 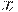и 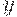, взятых отдельно, к 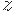. Упорядочение элементовмножества 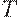с заданным таким способом нечетким отношением предлагается осуществлять в соответствии со значениями функции

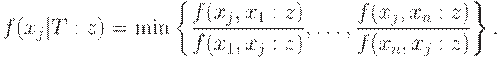
Максимальным в смысле этого упорядочения является элемент 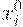такой, что

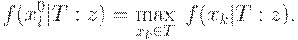
Для задачи о сходстве отца и детей значения этой функции таковы:

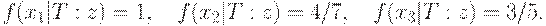
Отсюда вытекает, что наиболее похож на отца старший сын, затем следуют дочь и младший сын.

Нейронные сети

Введение

На заре развития электронно-вычислительной техники в середине ХХ века среди ученых и конструкторов еще не существовало единого мнения о том, как должна быть реализована и по какому принципу работать типовая электронно-вычислительная машина. Это сейчас общепринятой является архитектура машины фон Неймана, по которой построены практически все существующие сегодня компьютеры. При этом в тех же учебниках ни слова не говорится о том, что в те же годы были предложены принципиально иные архитектуры и принципы действия компьютеров. Одна из таких схем получила название нейросетевого компьютера, или просто нейросети.

Нейросетевой подход к созданию искусственного интеллекта состоит в проектировании механизмов имитации процесса передачи сигналов в биологическом мозге. Первый интерес к нейросетям был обусловлен пионерской работой МакКаллока и Питса, изданной в 1943 году, где предлагалась схема компьютера, основанного на аналогии с работой человеческого мозга. Они создали упрощенную модель нервной клетки – нейрон. На рис. 1 изображена упрощенная модель биологического мозга. Мозг человека состоит из белого и серого веществ: белое – это тела нейронов, а серое – это соединительная ткань между нейронами, или аксоны и дендриты.

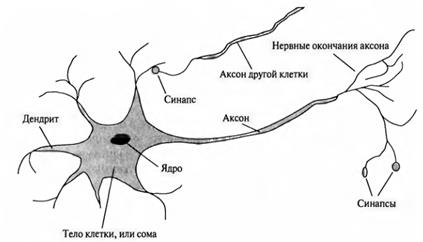
Нейрон состоит из тела и отростков, обычно одного длинного отростка - АКСОНА и нескольких коротких разветвленных отростков ‑ ДЕНДРИТОВ. Аксоны и дендриты соединяют нейроны друг с другом с целью передачи сигналов. По дендритам импульсы следуют к телу клетки, по аксону ‑ от тела клетки к другим нейронам. Место соединения аксонов и дендритов называется СИНАПСОМ.

Биологический мозг состоит из огромного числа (примерно 10¹¹) нейронов, связанных между собой. Нейроны действуют как процессоры передачи сигнала, каждый нейрон получает информацию через свои дендриты, а передает ее дальше – к другим нейронам только через единственный аксон, разветвляющийся на конце на тысячи синапсов.

Простейший нейрон может иметь до 10000 дендритов, принимающих сигналы от других клеток.

Таким образом, мозг содержит примерно 10¹⁵ взаимосвязей. Если учесть, что любой нейрофизиологический процесс активизирует сразу множество нейронов, то можно представить себе то количество информации или сигналов, которое возникает в мозгу.

Нейроны взаимодействуют посредством серий импульсов, длящихся несколько миллисекунд, каждый импульс представляет собой частотный сигнал с частотой от нескольких единиц до сотен герц. Это невообразимо медленно по сравнению с современными компьютерами, но в тоже время человеческий мозг гораздо быстрее машины может обрабатывать аналоговую информацию, как-то: узнавать изображения, чувствовать вкус, узнавать звуки, читать чужой почерк, оперировать качественными параметрами. Все это реализуется посредством сети нейронов, соединенных между собой синапсами. Другими словами, мозг -–это система из параллельных процессоров, работающая гораздо эффективнее, чем популярные сейчас последовательные вычисления.

Что из себя представляет нейронная сеть (НС)? Исходя из названия — сеть представляет из себя совокупность нейронов, соединенных друг с другом определенным образом. Каждый нейрон представляет из себя элемент, который вычисляет выходной сигнал (по определенному правилу) из совокупности входных сигналов. То есть основная последовательность действий одного нейрона такая:

· Прием сигналов от предыдущих элементов сети

· Комбинирование входных сигналов

· Вычисление выходного сигнала

· Передача выходного сигнала следующим элементам нейронной сети

Между собой нейроны могут быть соединены абсолютно по-разному, это определяется структурой конкретной сети. Но суть работы нейронной сети остается всегда одной и той же. По совокупности поступающих на вход сети сигналов на выходе формируется выходной сигнал (или несколько выходных сигналов). То есть нейронную сеть упрощенно можно представить в виде черного ящика, у которого есть входы и выходы. А внутри этого ящика сидит огромное количество нейронов.

Эту упрощенную модель можно считать метафорой для представления искусственных нейронных сетей (ИНС), осуществляемого с использованием электрических и электронных аппаратных средств и программного обеспечения, как показано на рис. 2.

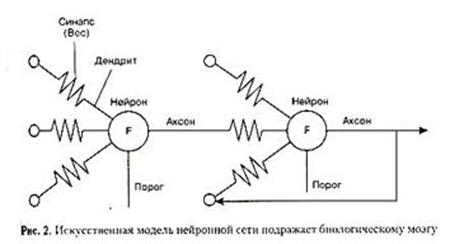
В теории ИНС обычно опускается такой компонент нейрона, как дендрит и считается, что входами ячейки нейрона являются непосредственно Синапсы, а выходом – аксон.

Далее под нейроном будет подразумеваться искусственный нейрон, то есть ячейка нейронной сети (НС). Нейрон характеризуется своим состоянием и, по аналогии с реальным нейроном, может быть либо возбуждён — либо заторможен.

Нейрон обладает группой синапсов – однонаправленных входных связей, соединенных с выходами других нейронов, а также имеет аксон – выходную связь данного нейрона, с которой сигнал (возбуждения или торможения) поступает на синапсы следующих нейронов. Общий вид нейрона приведен на рисунке 3. Каждый синапс характеризуется величиной синаптической связи или ее весом w_i

По физическому смыслу, вес синоптической связи – это электрическая проводимость данного синапса.

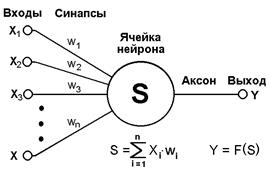
Текущее состояние нейрона определяется, как взвешенная сумма его входов:

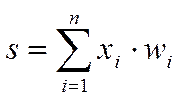
Значение на входе синапса умножается на вес данного синапса, потом все эти значения суммируются и получаем текущее состояние нейрона.

МакКаллок и Питтс [W.S. McCulloch and W. Pitts, "A logical Calculus of Ideas Immanent in Nervous Activity", Bull. Mathematical Biophysics, Vol. 5, 1943, pp. 115-133] предложили использовать бинарный пороговый элемент в качестве модели искусственного нейрона. Этот математический нейрон вычисляет взвешенную сумму n входных сигналов x_j, j = 1, 2... n, и формирует на выходе сигнал величины 1, если эта сумма превышает определенный порог u, и 0 - в противном случае.

Часто удобно рассматривать u как весовой коэффициент, связанный с постоянным входом x₀ = 1. Положительные веса соответствуют возбуждающим связям, а отрицательные - тормозным. МакКаллок и Питтс доказали, что при соответствующим образом подобранных весах совокупность параллельно функционирующих нейронов подобного типа способна выполнять универсальные вычисления. Здесь наблюдается определенная аналогия с биологическим нейроном: передачу сигнала и взаимосвязи имитируют аксоны и дендриты, веса связей соответствуют синапсам, а пороговая функция отражает активность сомы.

Выход нейрона есть функция его состояния: Y = F(S)

Нелинейная функция F называется активационной и может иметь различный вид, как показано на рисунке 4.

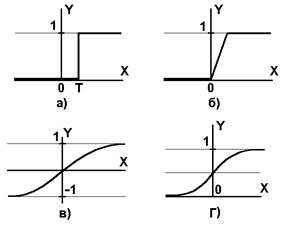
Рис.4 а) функция единичного скачка; б) линейный порог (гистерезис);
в) сигмоид – гиперболический тангенс; г) сигмоид – формула (3)

Одной из наиболее распространенных является нелинейная функция с насыщением, так называемая логистическая функция или сигмоид (т.е. функция S-образного вида):

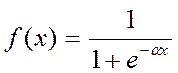
При уменьшении a сигмоид становится более пологим, в пределе при a=0 вырождаясь в горизонтальную линию на уровне 0.5, при увеличении a сигмоид приближается по внешнему виду к функции единичного скачка с порогом T в точке x=0. Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне [0,1].

Одна из причин, по которой сигмоид используется в нейронных сетях, это простое выражение его производной через саму функцию (которое и позволило существенно сократить вычислительную сложность метода обратного распространения ошибки, сделав его применимым на практике):

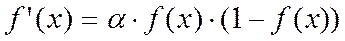
Вычисление производной необходимо, потому что для корректировки весовых коэффициентов при обучении ИНС с помощью алгоритма обратного распространения, используется метод градиентного спуска.

Формально, искусственный нейрон – является однослойным перцептроном (персептроном), т.е. моделью, в которой входные элементы напрямую соединены с выходными с помощью системы весов, и выполняет функцию линейной классификации.

Классификация – это процесс группировки/разбиения объектов исследования или наблюдения в соответствии с их общими признаками.

Линейный классификатор — это один из самых простых алгоритмов классификации.

В задачах с двумя классами (бинарная классификация) линейный классификатор — это гиперплоскость, разделяющая n-мерное пространство признаков на два класса (полупространства). Т.е. нейрон (линейный классификатор) определяет — входные данные относятся либо к группе A, либо к группе B. Это можно представить, если рассмотреть линию в 2-мерном пространстве. Точки в этом пространстве могут быть классифицированы, как лежащие либо по одну сторону этой линии, либо по другую.

Однослойный перцептрон хорош для решения задач линейной классификации, т.е. именно для случая двумерного пространства и классифицирующей линии, но он не сможет решить задачу, которая не может быть решена линейным разделением.

Классический пример задачи, которая не по зубам однослойному перцептрону — исключающее ИЛИ (XOR — exclusive OR).

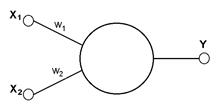
Рис.5 Однонейронный перцептрон

Однослойный перцептрон, состоящий из одного нейрона с двумя входами, представленный на рисунке 5, не способен разделить плоскость (двумерное гиперпространоство) на две полуплоскости так, чтобы осуществить классификацию входных сигналов по классам 0 и 1 в соответствии с логической функцией XOR.

Рассмотрим точки (0,0), (1,0), (0,1), и (1,1) в пространстве.

Для XOR, не существует способа провести одну линию, которая отделяет точки TRUE: (1,0) и (0,1) от точек FALSE: (0,0) и (1,1).

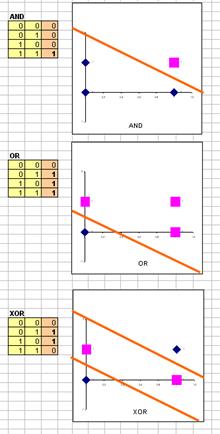
Т.о. точки XOR линейно неразделимы.Выходит, однослойный перцептрон не может быть обучен, для разделения по XOR. Чтобы решить проблему XOR, нужно создать многослойный перцептрон!