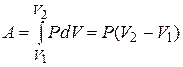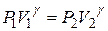Применение 1-го начала термодинамики к изопроцессам идеального газа
(Изопроцессы от 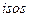 (греч.) – равный). Процессы, происходящие при каком-то постоянном параметре (
(греч.) – равный). Процессы, происходящие при каком-то постоянном параметре ( 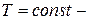 изотермический;
изотермический; 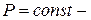 изобарический;
изобарический; 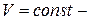 изохорический).
изохорический).
Теплоёмкостью 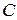 тела называется величина, равная отношению сообщённого телу количества теплоты
тела называется величина, равная отношению сообщённого телу количества теплоты 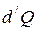 к соответствующему приращению температуры
к соответствующему приращению температуры 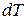 .
.
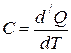
|
Размерность теплоёмкости тела 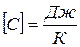 .
.
Аналогичные определения вводятся для 1 моля (молярная теплоёмкость
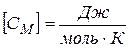 ), и для единицы массы вещества
), и для единицы массы вещества 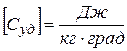 .
.
1. Рассмотрим нагревание газа при постоянном объёме. По первому закону термодинамики:
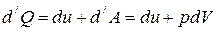 , т.к.
, т.к. 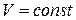 , то
, то 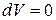 .
.
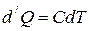 по определению, а для процесса с
по определению, а для процесса с 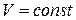 :
:
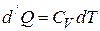 , где
, где
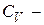 теплоёмкость газа при постоянном объёме.
теплоёмкость газа при постоянном объёме.
Тогда 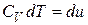 и
и
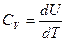
|
2. Теплоёмкость газа при постоянном давлении:
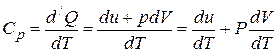 .
.
Для идеального газа для 1 моля (из уравнения Менделеева-Клапейрона).
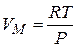 .
.
Продифференцируем это выражения по температуре Т, получим:
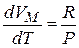 , получим для 1 моля
, получим для 1 моля
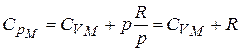
|
Но выражение называется уравнением Майера. Оно показывает, что 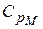 всегда больше
всегда больше 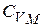 на величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении по сравнению с процессом при постоянном объёме, требуется ещё дополнительное количество теплоты на совершение работы расширения газа, т.к. постоянство давления обеспечивается увеличением объёма газа.
на величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении по сравнению с процессом при постоянном объёме, требуется ещё дополнительное количество теплоты на совершение работы расширения газа, т.к. постоянство давления обеспечивается увеличением объёма газа.
3. При адиабатическом процессе (процесс протекающий без теплообмена с внешней средой).
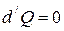 ,
, 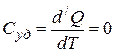 , т.е. теплоёмкость в адиабатическом процессе равна нулю.
, т.е. теплоёмкость в адиабатическом процессе равна нулю.
4. При изотермическом процессе 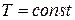 ,
, 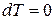 , и, следовательно, теплоёмкость
, и, следовательно, теплоёмкость 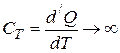 .
.
Существуют процессы, при которых газ, расширяясь, совершает работу большую, чем полученная теплота, тогда его температура понижается, несмотря на приток теплоты. Теплоёмкость в этом случае отрицательна. В общем случае 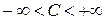 .
.
3. Работа, совершаемая газом при изопроцессах
Изобарный 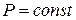 .
.
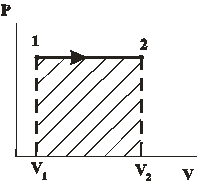
| Диаграмма этого процесса (изобары) в координатах 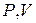 изображается прямой, параллельной оси изображается прямой, параллельной оси 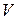 (рис. 14.2). При изобарном процессе работа газа при расширении объёма от (рис. 14.2). При изобарном процессе работа газа при расширении объёма от 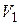 до до 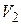 равна: равна:
| |
| Рис. 14.2 |
И определяется площадью заштрихованного прямоугольника на рис. 14.2.
Изохорный процесс ( 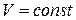 ). Диаграмма этого процесса
). Диаграмма этого процесса
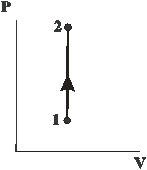
| (изохора) в координатах 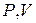 изображается прямой, параллельной оси ординат (рис. 14.3). поскольку изображается прямой, параллельной оси ординат (рис. 14.3). поскольку 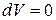 , то , то 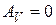 .
Изотермический процесс ( .
Изотермический процесс ( 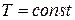 ). (рис. 14.4). Воспользовавшись уравнением состояния идеального газа Менделеева- Клайперона для работы в изотермическом процессе получаем: ). (рис. 14.4). Воспользовавшись уравнением состояния идеального газа Менделеева- Клайперона для работы в изотермическом процессе получаем:
| ||
| Рис. 14.3 | |||
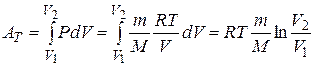
| |||
Изотермический процесс является идеальным процессом, т.к. расширение газа при постоянной температуре может происходить только бесконечно медленно. При конечной скорости расширения возникнут градиенты температуры.
4. Адиабатический (адиабатный) процесс
Это процесс, происходящий без теплообмена с окружающими телами. Рассмотрим, при каких условиях можно реально осуществить адиабатический процесс, или приблизиться к нему.
1. Необходима адиабатическая оболочка, теплопроводность которой равна нулю. Приближением к такой оболочке может служить сосуд Дьюара.
2. 2-ой случай – процессы, протекающие очень быстро. Теплота не успевает распространиться и в течение некоторого времени можно полагать 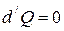 .
.
3. Процессы, протекающие в очень больших объёмах газа, например, в атмосфере (области циклонов, антициклонов). Для выравнивания температуры передача теплоты должна происходить из соседних, более нагретых слоёв воздуха, на это часто требуется значительное время.
Для адиабатического процесса первый закон термодинамики:
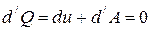
или 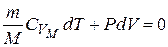 .
.
В случае расширения газа 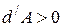 ,
, 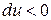 , (температура понизится). Если произошло сжатие газа
, (температура понизится). Если произошло сжатие газа 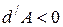 , то
, то 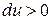 (температура повышается). Выведем уравнение, связывающее параметры газа при адиабатическом процессе. Учтём, что для идеального газа
(температура повышается). Выведем уравнение, связывающее параметры газа при адиабатическом процессе. Учтём, что для идеального газа 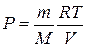 , тогда
, тогда
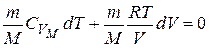
Разделим обе части уравнения на 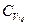 :
:
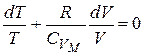 .
.
Из уравнения Майера 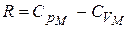 , тогда
, тогда
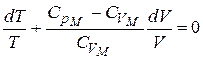 .
.
Обозначим 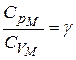 .
.
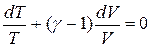 .
.
Проинтегрируем это уравнение:
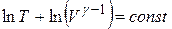
|
Отсюда
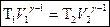
Получили уравнение Пуассона (для адиабаты) (1 – ая форма). Заменим 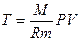 :
:
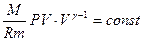 ,
,
| т.к. для данной массы газа 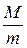 величина постоянная, то величина постоянная, то
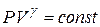
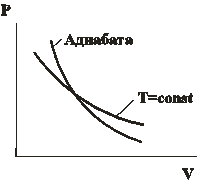
2 – ая форма уравнения Пуассона. На рис. 14.5 представлены сравнительные графики изотермы и адиабаты. | |
| Рис. 14.5 |
Так как 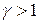 , то график адиабаты более крутой по сравнению с изотермой. Вычислим работу при адиабатическом процессе:
, то график адиабаты более крутой по сравнению с изотермой. Вычислим работу при адиабатическом процессе:
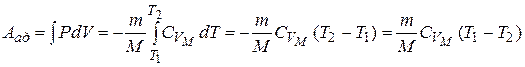
т.е 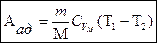
Политропические процессы.
Так называют процессы, уравнение которых в переменных 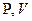 имеет вид
имеет вид
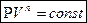
где n-произвольное число, как положительное, так и отрицательное, а также равное нулю. Соответствующую кривую называют политропой. Политропическими являются, в частности, процессы адиабатический, изотермический, изобарический, изохорический.
Вопросы для самоконтроля
1. Чем термодинамический метод исследования свойств систем отличается от молекулярно-кинетического?
2. Какую часть энергии системы называют внутренней?
3. Как определяется работа в термодинамике?
4. Что называется количеством теплоты?
5. Какая из величин А, Q,U является функцией состояния термодинамической системы? Почему?
6. Сформулируйте первое начало термодинамики.
7. Запишите первое начало термодинамики для всех известных вам изопроцессов идеального газа.
8. Что такое теплоемкость тела? Чем отличаются удельная и молярная теплоемкости?
9. Чему равна теплоемкость для каждого изопроцесса? Почему теплоемкость 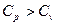 ?
?
10. Получите выражение для работы в каждом процессе. При каком изо- процессе не совершается работа?
11. Какой процесс называется адиабатным? Как можно осуществить процесс, близкий к адиабатному?
12. Проделайте вывод уравнения Пуассона для адиабатного процесса.
Лекция №15
Дата добавления: 2016-12-27; просмотров: 1464;