Обратимые и необратимые процессы
Пусть в результате некоторого процесса в изолированной системе тело переходит из состояния А в состояние В и затем возвращается в начальное состояние А. Процесс называется обратимым, если возможно осуществить обратный переход из В в А через те же промежуточные состояния, что и в прямом процессе, чтобы не осталось никаких изменений и в самом теле и в окружающих телах. Если же обратный процесс невозможен, или по окончании процесса в окружающих телах и в самом теле остались какие-либо изменения, то процесс является необратимым.
Примеры необратимых процессов. Любой процесс сопровождаемый трением является необратимым (теплота, выделяющаяся при трении не может без затраты работы другого тела собраться и вновь превратиться в работу). Все процессы, сопровождаемые теплопередачей от нагретого тела к менее нагретому, является необратимыми (например, теплопроводность). К необратимым процессам также относятся диффузия, вязкое течение. Все необратимые процессы являются неравновесными.
Равновесные – это такие процессы, которые представляют из себя последовательность равновесных состояний. Равновесное состояние – это такое состояние, в котором без внешних воздействий тело может находиться сколь угодно долго. (Строго говоря, равновесный процесс может быть только бесконечно медленным. Любые реальные процессы в природе протекают с конечной скоростью и сопровождаются рассеянием энергии. Обратимые процессы – идеализация, когда необратимыми процессами можно пренебречь).
Круговой процесс (цикл). Если тело из состояния А в состояние В переходит через одни промежуточные состояния, а возвращается в начальное состояние А через другие промежуточные состояния, то совершается круговой процесс, или цикл.
Круговой процесс является обратимым, если все его части обратимы. Если какая-либо часть цикла необратима, то и весь процесс необратим.
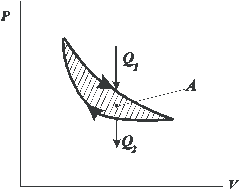
| Различают прямой цикл, или цикл тепловой машины и обратный цикл, или цикл холодильной машины (о нём в вопросе № 3).
Совершенная за цикл работа равна разности между количеством теплоты, полученной телом при расширении и количество теплоты, отданным при сжатии. Работа в  координатах равна площади цикла (рис. 15.1): координатах равна площади цикла (рис. 15.1):
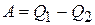 . .
|
| Рис. 15.1 |
2. Цикл Карно и его КПД для идеального газа
(Сади Карно (1796 – 1832) – французский физик).
 Рис. 15.2
Рис. 15.2
| Цикл Карно заключается в следующем. Сначала система, имея температуру 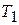 , приводится в тепловой контакт с нагревателем. Затем, бесконечно медленно уменьшая внешнее давление, её заставляют расширяться по изотерме 1-2. При этом она получает тепло , приводится в тепловой контакт с нагревателем. Затем, бесконечно медленно уменьшая внешнее давление, её заставляют расширяться по изотерме 1-2. При этом она получает тепло 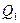 от нагревателя и производит работу от нагревателя и производит работу 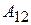 против внешнего давления. против внешнего давления.
|
Рабочий цикл состоит из двух равновесных изотерм и двух равновесных адиабат (рис. 15.2). В машине, как допускают, отсутствуют потери на трение, теплопроводность и т.д. С машиной связаны два резервуара теплоты. Один, имеющий температуру 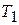 , называется нагревателем, другой имеющий более низкую температуру
, называется нагревателем, другой имеющий более низкую температуру 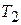 – холодильником (или теплоприёмником). Резервуары настолько велики, что отдача или получение теплоты не изменяет их температуру.
– холодильником (или теплоприёмником). Резервуары настолько велики, что отдача или получение теплоты не изменяет их температуру.
После этого систему адиабатически изолируют и заставляют расширяться по адиабате 2 – 3, пока её температура не достигает температуры холодильника 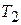 . При адиабатическом расширении система также совершает некоторую работу против внешнего давления. В состоянии 3 систему приводят в тепловой контакт с холодильником и непрерывным увеличением давления изотермически сжимают её до некоторого состояния 4. При этом над системой производится работа (т.е. сама система совершает отрицательную работу
. При адиабатическом расширении система также совершает некоторую работу против внешнего давления. В состоянии 3 систему приводят в тепловой контакт с холодильником и непрерывным увеличением давления изотермически сжимают её до некоторого состояния 4. При этом над системой производится работа (т.е. сама система совершает отрицательную работу  ), и она отдаёт холодильнику некоторое количество тепла
), и она отдаёт холодильнику некоторое количество тепла 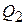 . Состояние 4 выбирается так, чтобы можно было сжатием по адиабате 4 – 1 вернуть систему в исходное состояние. Для этого над системой надо совершить работу
. Состояние 4 выбирается так, чтобы можно было сжатием по адиабате 4 – 1 вернуть систему в исходное состояние. Для этого над системой надо совершить работу 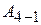 (система должна произвести отрицательную работу
(система должна произвести отрицательную работу 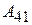 ). В результате кругового процесса Карно внутренняя энергия системы не изменяется, поэтому произведённая работа
). В результате кругового процесса Карно внутренняя энергия системы не изменяется, поэтому произведённая работа 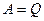
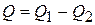
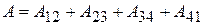 .
.
Рассчитаем коэффициент полезного действия идеальной тепловой машины, работающей по циклу Карно. Эта величина равна отношению количества теплоты, превращённого в работу, к количеству теплоты, полученному от нагревателя.
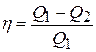
|
Полезная работа за цикл равна сумме всех работ отдельных частей цикла:
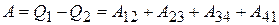 .
.
Работа изотермического расширения:
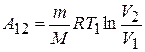 ,
,
адиабатического расширения:
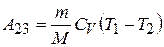 ,
,
изотермического сжатия:
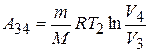 ,
,
адиабатического сжатия:
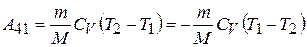 .
.
Адиабатические участки цикла не влияют на общий результат, т.к. работы на них равны и противоположны по знаку, следовательно 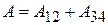 .
.
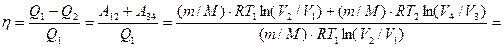
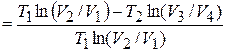 . (1)
. (1)
Так как состояния газа, описываемые точками 2 и 3 лежат на одной адиабате, то параметры газа связаны уравнением Пуассона:
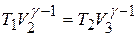 .
.
Аналогично для точек 4 и 1:
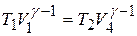
Разделив почленно эти уравнения, получим:
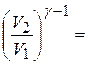
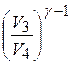
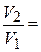
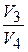 , тогда из (1) получается
, тогда из (1) получается
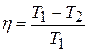
|
То есть КПД цикла Карно определяется только температурами нагревателя и холодильника.
Теорема Карно (без доказательства): КПД всех обратимых машин, работающих при одних и тех же температурах нагревателя и холодильника одинаков и определяется только температурами нагревателя и холодильника.
Замечание: КПД реальной тепловой машины всегда ниже, чем КПД идеальной тепловой машины (в реальной машине существуют потери тепла, которые не учитываются при рассмотрении идеальной машины).
3. Принцип действия теплового двигателя и холодильной машины
Любой тепловой двигатель состоит из 3-х основных частей: рабочего тела, нагревателя и холодильника.
Рабочее тело получает некоторое количество теплоты 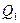 , от нагревателя. При сжатии газ передаёт некоторое количество теплоты
, от нагревателя. При сжатии газ передаёт некоторое количество теплоты 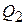 холодильнику. Полученная работа, совершаемая двигателем за цикл:
холодильнику. Полученная работа, совершаемая двигателем за цикл:
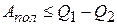
| (неравенство – характеризует реальные машины, равенство для идеальных машин). |
(Замечание: реальные тепловые двигатели обычно работают по так называемому разомкнутому циклу, когда газ после расширения выбрасывается, и сжимается новая порция. Однако это существенно не влияет на термодинамику процесса. В замкнутом цикле расширяется и сжимается одна и та же порция.).
Холодильная машина. Цикл Карно обратим, следовательно, его можно провести в обратном направлении. (4-3-2-1-4 (рис.15.3)) От холодильной камеры поглощается тепло 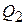 .
.
| Нагревателю рабочее тело передаёт некоторое количество теплоты  . Внешние силы совершают работу . Внешние силы совершают работу 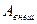 , тогда , тогда
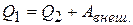 В результате цикла некоторое количество теплоты переходит от холодного тела к телу с более высокой температурой.
Реально рабочим телом в холодильной установке обычно служат пары легкокипящих жидкостей – аммиак, фреон и т. п. К машине подводится энергия от
В результате цикла некоторое количество теплоты переходит от холодного тела к телу с более высокой температурой.
Реально рабочим телом в холодильной установке обычно служат пары легкокипящих жидкостей – аммиак, фреон и т. п. К машине подводится энергия от
|
| Рис. 15.3 |
электрической сети. За счёт этой энергии и совершается процесс “передачи теплоты” от холодильной камеры к более нагретым телам (к окружающей среде).
Эффективность холодильной установки оценивается по холодильному коэффициенту:
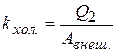
|
Тепловой насос. Это непрерывно действующая машина, которая за счёт затрат работы 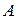 (электроэнергии) отбирает тепло
(электроэнергии) отбирает тепло 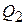 от источника с низкой температурой
от источника с низкой температурой 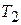 (чаще всего близкой к температуре окружающей среды) и передаёт источнику тепла с более высокой температурой
(чаще всего близкой к температуре окружающей среды) и передаёт источнику тепла с более высокой температурой 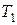 количество теплоты
количество теплоты 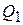 , равна сумме тепла, отобранного от низкотемпературного источника и затраченной работы:
, равна сумме тепла, отобранного от низкотемпературного источника и затраченной работы: 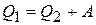 .
.
| “Отопительный” коэффициент |
|
всегда больше единицы (максимально возможный 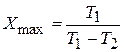 ).
).
Для сравнения: если отапливать помещение с помощью обычных электронагревателей, то количество теплоты, выделенное в нагревательных элементах, в точности равно расходу электроэнергии.
4. Энтропия. Закон возрастания энтропии
В термодинамике понятие “энтропия” было введено немецким физиком Р. Клаузиусом (1865 г.).
Из статической физики: отношение количества теплоты 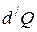 , сообщаемого системе, к температуре
, сообщаемого системе, к температуре 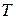 (системы) есть приращение некоторой функции состояния
(системы) есть приращение некоторой функции состояния 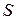 (энтропий).
(энтропий).
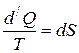
| 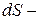 полный дифференциал функции состояния полный дифференциал функции состояния 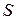 , названной энтропией. (греч. , названной энтропией. (греч.  поворот, превращение) поворот, превращение)
|
Каждое состояние тела характеризуется определённым значением энтропии 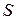 . Если обозначить энтропию в состояниях 1 и 2 как
. Если обозначить энтропию в состояниях 1 и 2 как 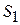 и
и 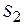 , то по определению для обратимых процессов:
, то по определению для обратимых процессов:
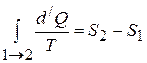
|
Значение произвольной постоянной, с которой определена энтропия, не играет роли. Физический смысл имеет не сама энтропия, а разность энтропий.
Закон возрастания энтропии.
Допустим, что изолированная система переходит из равновесного
| состояния 1 в равновесное состояние 2, но процесс перехода 1 – 2 является необратимым – на рисунке 15.4 обозначен пунктиром. Обратный переход обратимый. Воспользуемся неравенством Клаузиуса (без вывода). | 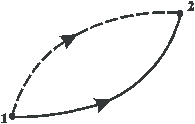
|
| Рис. 15.4 |
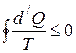
|
(для обратного процесса знак “=” , для необратимого “<”).
Для нашего перехода 1 – 2 – 1 :
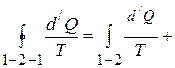
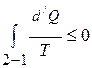 .
.
Так как процесс 2 – 1 обратимый, то будет равенство
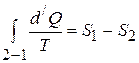 , отсюда
, отсюда
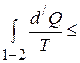
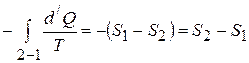 .
.
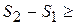 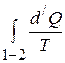
|
Под температурой 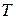 понимается температура системы, при которой она отдаёт или принимает тепло
понимается температура системы, при которой она отдаёт или принимает тепло 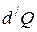 .
.
Если система адиабатически изолирована, то 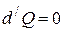 и
и
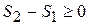
|
Таким образом, энтропия адиабатически изолированной системы не может убывать, она либо возрастает, либо остаётся постоянной. (Закон возрастания энтропии).
5. Статистический вес (термодинамическая вероятность).
Под термодинамической вероятностью понимается число микросостояний (микрораспределений, например, распределений молекул по пространству или энергии) которыми может определяться рассматриваемое макрораспределение.

| Пример. Имеется сосуд, состоящий из двух частей, в котором может находится 4 молекулы. Сколькими способами можно распределить эти молекулы, чтобы в левой части была одна молекула, а в правой– три молекулы? Могут быть следующие варианты: в левой части 1-ая молекула, а 2-я, |
| Рис. 15.5 |
3-я и 4-я – в первой и т.д. ( рис. 15.5).
Число распределений можно подсчитать следующим образом:
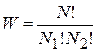 , ,
|
где 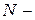 общее число молекул,
общее число молекул, 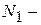 число молекул в 1 – ой части сосуда,
число молекул в 1 – ой части сосуда, 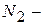 во второй. Термодинамическая вероятность в рассматриваемом примере.
во второй. Термодинамическая вероятность в рассматриваемом примере.
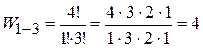
Аналогично для распределения 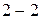 :
:
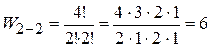 .
.
Для 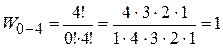 .
.
Заметим, что наибольшая термодинамическая вероятность у равномерного распределения, оно может осуществляться наибольшим числом способов.
Связь энтропии с вероятностью была установлена Больцманом, постулировавшим, что энтропия пропорциональна логарифму вероятности состояния
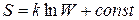 , ,
|
(энтропия определяется с точностью до константы
const),
где 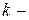 константа Больцмана,
константа Больцмана, 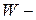 термодинамическая вероятность.
термодинамическая вероятность.
Дата добавления: 2016-12-27; просмотров: 1691;